一、本周周赛总结

• T1 模拟。
• T2 贪心。
• T3 DP类似LIS，构造路径方案。
• T4 分组前缀和优化的分组背包求方案数。
  

100095. 上一个遍历的整数

100095. 上一个遍历的整数

1. 题目描述

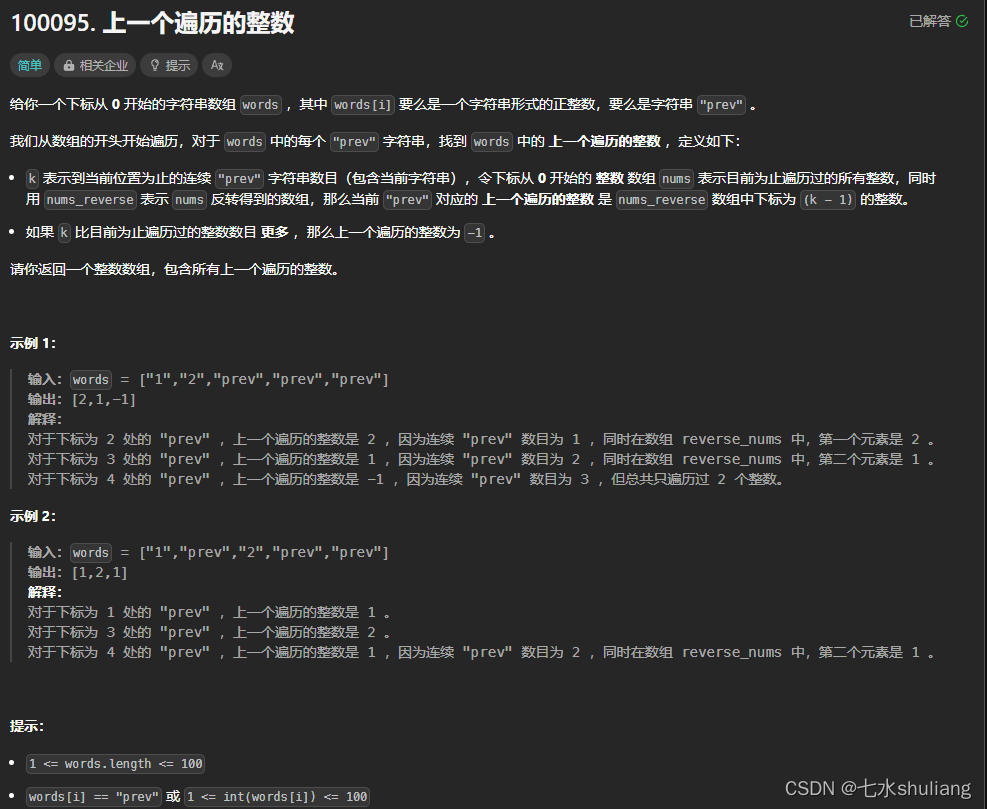
2. 思路分析

按题意模拟即可。

3. 代码实现

class Solution:def lastVisitedIntegers(self, words: List[str]) -> List[int]:ans = []nums = []k=0for v in words:if v[0].isdigit():nums.append(int(v))k = 0 else:k += 1 if k > len(nums):ans.append(-1)else:ans.append(nums[-k])return ans 

100078. 最长相邻不相等子序列 I

100078. 最长相邻不相等子序列 I

1. 题目描述

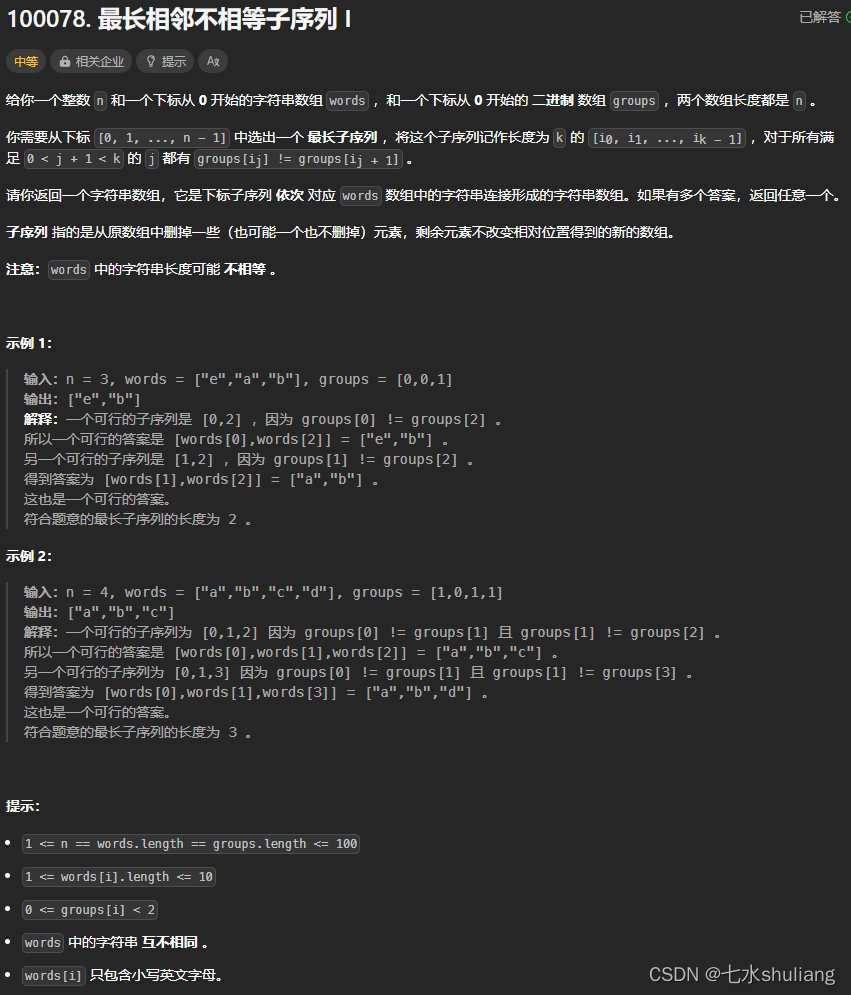
2. 思路分析

方法1

• 枚举第一个g是0还是1，然后贪心的向后取位置。

---

方法2

• 直接pairwise，相邻不同了，则可以取左边的，注意记得取最后一个。

3. 代码实现

class Solution:def getWordsInLongestSubsequence(self, n: int, words: List[str], groups: List[int]) -> List[str]:def f(s):ans = [0,[]]for w, g in zip(words,groups):if g == s:ans[0]+=1ans[1].append(w)s ^= 1 return ansreturn max(f(0),f(1))[1]

100077. 最长相邻不相等子序列 II

100077. 最长相邻不相等子序列 II

1. 题目描述

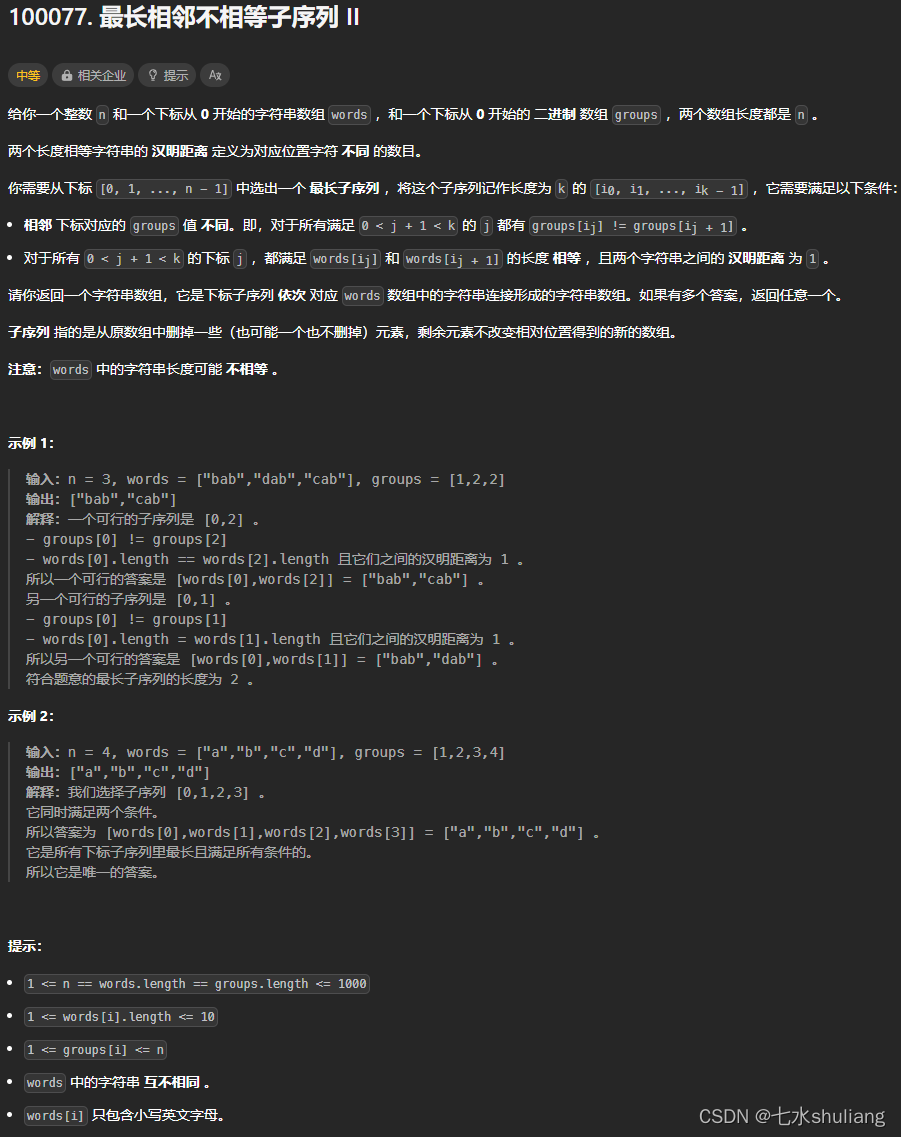
2. 思路分析

• n方dp。
• 从前边满足的地方转移过来，注意记录一个from_index来储存路径。

3. 代码实现

def han(s, t):return sum(x!=y for x,y in zip(s,t))
class Solution:def getWordsInLongestSubsequence(self, n: int, words: List[str], groups: List[int]) -> List[str]:f = [1]*n from_index = [-1]*nfor i, (w, g) in enumerate(zip(words,groups)):for j in range(i):if g != groups[j] and len(w) == len(words[j]) and han(words[j], w) == 1 and f[j] >= f[i]:f[i] = f[j] + 1from_index[i] = ji = f.index(max(f))ans = []while i != -1:ans.append(words[i])i = from_index[i]return ans[::-1]                    

100029. 和带限制的子多重集合的数目

100029. 和带限制的子多重集合的数目

1. 题目描述

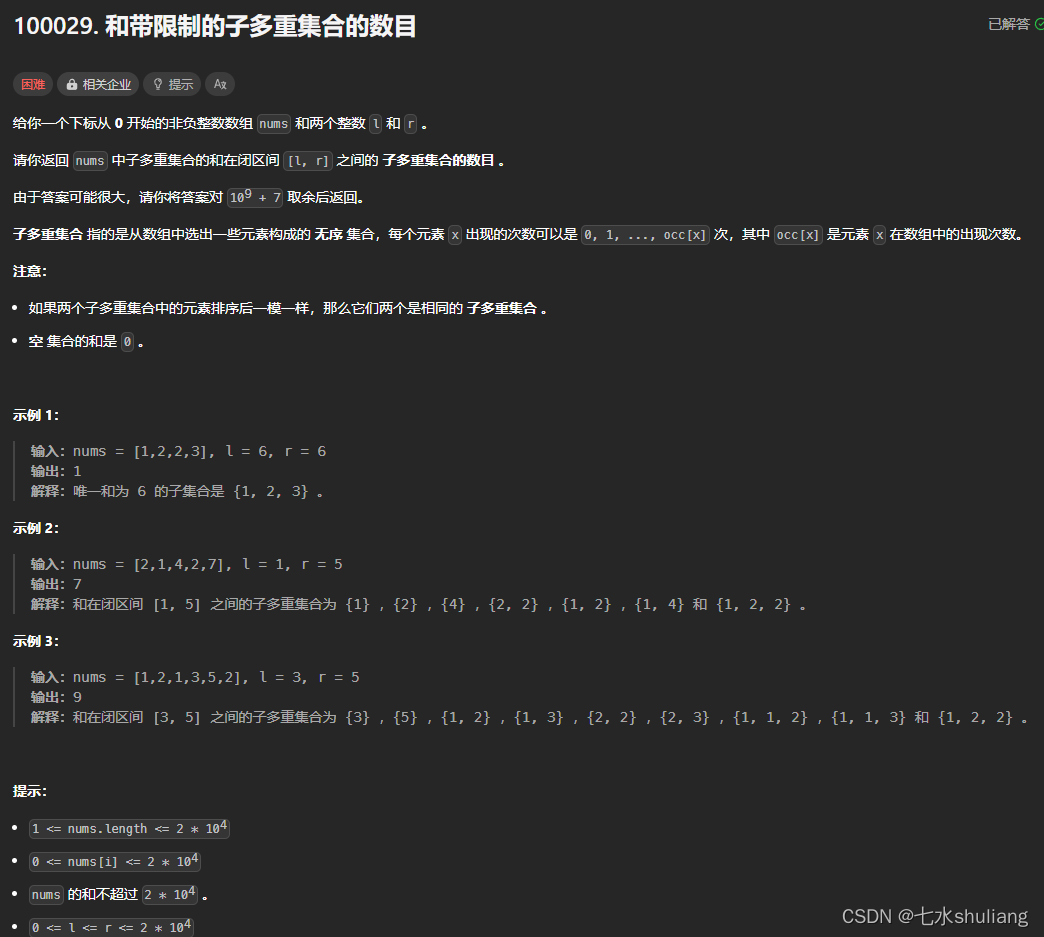
2. 思路分析

• 题目描述很复杂，但其实是分组背包求方案数。
• 这样的话，值域是2e4,物品数也是2e4。n方会TLE。
• 考虑优化，我们知道分组背包先遍历组，然后遍历体积，再遍历每组里的物品。
  • 可以看到内层，f[j] += f[j-k]+…f[j-k*c],这里累计了1~c,并且间隔是一样的，考虑用前缀和优化。
  • 可以用分组前缀和，类似滑窗。参考普通前缀和，我们向前边添加k个0，方便代码。
• 注意到，题目限制sum(nums)<=2e4,那么不同的数字最多有多少组呢？显然最小是1,2,3~，那么不同数字组最多是开方级别的。
• 因此复杂度变成了O(r√S)。

3. 代码实现

MOD = 10**9 + 7 
class Solution:def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:cnt = Counter(nums)f = [cnt[0]+1] + [0] * rs = 0for k, c in cnt.items():if k == 0:continues += k * c pre = [0]*k             for v in f:pre.append((v+pre[-k])%MOD)for j in range(min(s, r), 0, -1):# f[j] += f[j-k]+..f[j-k*c]f[j] += pre[j] - pre[max(j-k*c, 0)]f[j] %= MOD return sum(f[l:]) %MOD   

参考链接