525. 连续数组
525. 连续数组
题目描述:
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。

解题思路:
本题的元素只有0和1,根据题目意思,我们可以把题目看成找一段最长的子区间使得区间的0
和1的数量相同,我们可以对其优化将所有的0变成-1,这样这段区间的和就为0
也就是转化为在【0,i-1】这个区间内最长的和为0的子数组
我们依旧可以利用哈希表hash,我们还得处理一下默认前缀和为0的时候等于-1的时候
长度的计算:

解题思路:
class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int,int>hash;hash[0]=-1;int ret=0,sum=0;for(int i=0;i<nums.size();i++){sum+=nums[i]==0?-1:1;if(hash.count(sum))ret=max(ret,i-hash[sum]);else hash[sum]=i;}return ret;}
};1314. 矩阵区域和
1314. 矩阵区域和
题目描述:
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和:
i - k <= r <= i + k,j - k <= c <= j + k且(r, c)在矩阵内。
解题思路:
本题我们还是使用前缀和+哈希表,不过是二维前缀和
因为本题的计算的下标的范围可能会越界,因此我们可以min和max函数就行解决,这里的+1是因为需要进行下标匹配,下标匹配下面会讲;
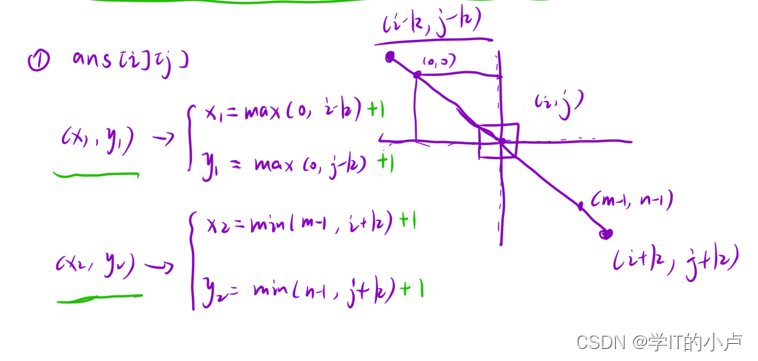
有个细节需要注意就是:
我们的mat数组是从0开始的,而我们的前缀和数组dp是从1开始,而我们返回的数组ans是从0开始的
因为力扣进行结果判断的时候需要从0开始,不然本题更加简单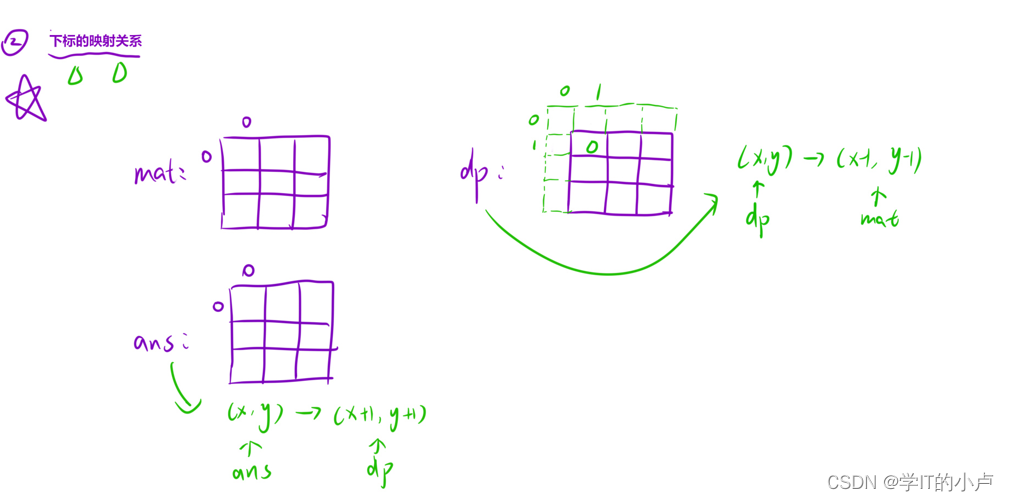
解题代码:
class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int n=mat.size();int m=mat[0].size();vector<vector<int>> dp(n+1,vector<int>(m+1));for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1];vector<vector<int>> ans(n,vector<int>(m));for(int i=0;i<n;i++){for(int j=0;j<m;j++){int x1=max(0,i-k)+1;int y1=max(0,j-k)+1;int x2=min(n-1,i+k)+1;int y2=min(m-1,j+k)+1;ans[i][j]=dp[x2][y2]-dp[x2][y1-1]-dp[x1-1][y2]+dp[x1-1][y1-1];}}return ans;}
};


![NSS [GWCTF 2019]枯燥的抽奖](https://img-blog.csdnimg.cn/img_convert/6e6f3634764d4f2616590c1569f66660.png)