5. 最长回文子串 - 力扣(LeetC5. 最长回文子串 - 力扣(LeetCode)5. 最长回文子串 - 力扣(LeetC
给你一个字符串 s,找到 s 中最长的回文子串。如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd" 输出:"bb"
一、「中心扩展法 + 双指针」
我的往期文章有详细介绍「中心扩展法 + 双指针」,大家感兴趣可以看一下:leetCode 647.回文子串 动态规划 + 优化空间 / 中心扩展法 + 双指针-CSDN博客![]() https://blog.csdn.net/weixin_41987016/article/details/133883091?spm=1001.2014.3001.5501
https://blog.csdn.net/weixin_41987016/article/details/133883091?spm=1001.2014.3001.5501
现在我们将用这个方法来解决本文中的此题:5. 最长回文子串 - 力扣(LeetCode)
class Solution {
public:vector<int> extend(string& s,int i,int j,int n) {while(i>=0 && j<n && s[i] == s[j]) {i--;j++;}return {i+1,j-1};}// 返回以 i, j 为中心的最长回文子串的左右边界string longestPalindrome(string s) {int n = s.size();vector<int> res{0,0};for(int i=0;i<n;i++) {vector<int> sub1 = extend(s,i,i,n);vector<int> sub2 = extend(s,i,i+1,n);if (res[1] - res[0] < sub1[1] - sub1[0]) res = sub1;if (res[1] - res[0] < sub2[1] - sub2[0]) res = sub2;}return s.substr(res[0], res[1] + 1 - res[0]);}
};- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
二、动态规划(详细可以看我的往期文章:leetCode 647.回文子串)
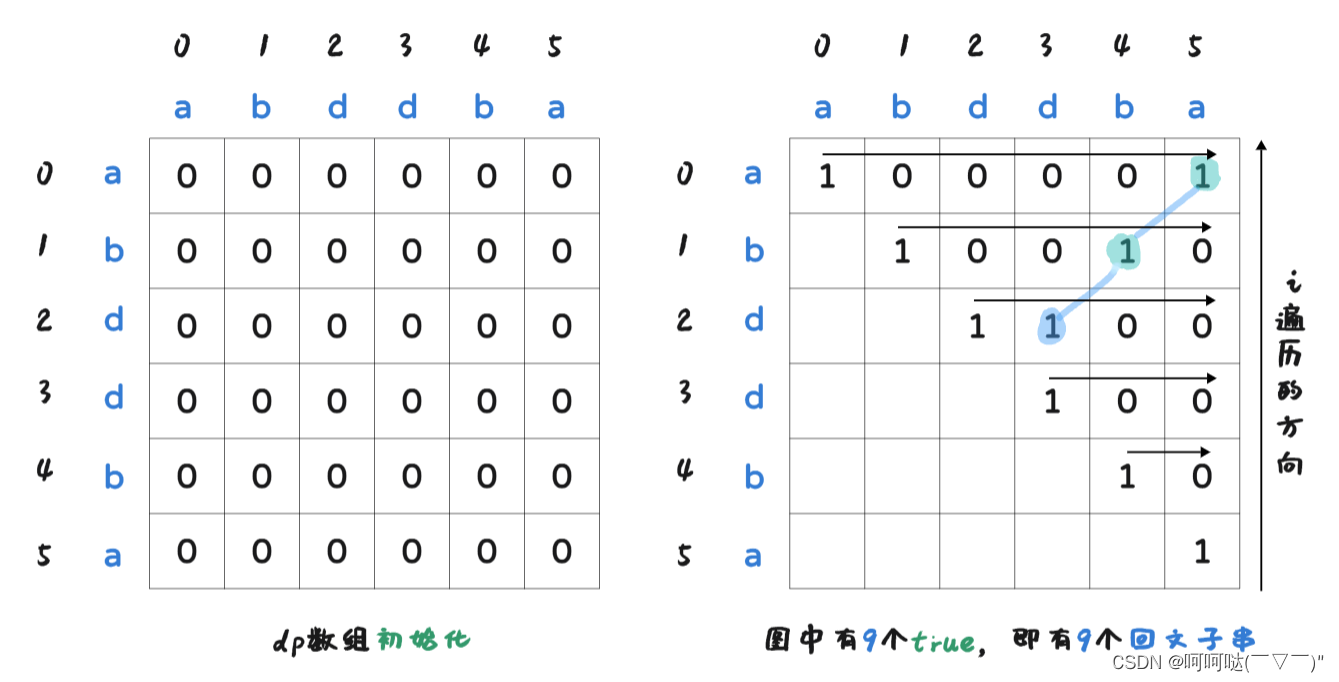
左边图是dp数组初始化,在填dp数组只会对右上三角进行数据更新,所以右边的图我就不画左下三角的0了。从图中,可得知有9个true,即有9个回文子串。还可以得知另一个信息,那就是回文子串有:"a","b","d","d","b","a","dd","bddb","abddba"
注:"dd"是回文子串的信息记录在(2,3)这个坐标,"bddb"是回文子串的信息记录在(1,4)这个坐标,"abddba"是回文子串的信息记录在(0,5)这个坐标,若为true,则该子串为回文。
(2,3),(1,4),(0,5)在左对角线上,所以观察的时候可以瞄准这条线上的坐标,分析信息
注:要明确和清晰dp[i][j] 表示区间范围[i,j]的子串是否为回文子串
这样就可以知道一个回文子串的起始和末尾,将其返回, 然后选取出最长回文子串
1.动态规划 二维dp
class Solution {
public:// 动态规划 二维dp string longestPalindrome(string s) {vector<vector<bool>> dp(s.size(),vector<bool>(s.size(),false));vector<int> res{0,0};for(int i=s.size()-1;i>=0;i--) {for(int j=i;j < s.size();j++) {if(s[i] == s[j] && (j-i<=1 || dp[i+1][j-1])) {dp[i][j] = true;if (res[1] - res[0] < j - i) res = {i,j};}}}return s.substr(res[0], res[1] + 1 - res[0]);}
};- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
2.动态规划 二维dp + 优化空间
class Solution {
public: // 动态规划 二维dp 优化空间string longestPalindrome(string s) {vector<vector<bool>> dp(2,vector<bool>(s.size(),false));vector<int> res{0,0};for(int i=s.size()-1;i>=0;i--) {for(int j=i;j < s.size();j++) {if(s[i] == s[j] && (j-i<=1 || dp[(i+1)%2][j-1])) {dp[i%2][j] = true;if (res[1] - res[0] < j - i) res = {i,j};}else {dp[i%2][j] = false;}}}return s.substr(res[0], res[1] + 1 - res[0]);}
};- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
3.动态规划 一维dp + 优化空间
class Solution {
public: // 动态规划 一维dp string longestPalindrome(string s) {vector<bool> dp(s.size(),false);vector<int> res{0,0};for(int i=s.size()-1;i>=0;i--) {bool pre = false;for(int j=i;j < s.size();j++) {bool tmp = dp[j];if(s[i] == s[j] && (j-i<=1 || pre)) {dp[j] = true;if (res[1] - res[0] < j - i) res = {i,j};}else {dp[j] = false;}pre = tmp;}}return s.substr(res[0], res[1] + 1 - res[0]);}
};- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
参考和推荐文章:
647. 回文子串 - 力扣(LeetCode)![]() https://leetcode.cn/problems/palindromic-substrings/solutions/1530868/by-lfool-2mvg/
https://leetcode.cn/problems/palindromic-substrings/solutions/1530868/by-lfool-2mvg/