一、问题描述

对于一个随机信号，我们可以通过统计手段，得到其的频次分布图（直方图），并由此计算出它的频率分布图。当观察次数区域无穷大时，频率分布图近似于概率密度函数。
下面我们以稳定分布的随机变量为例，来对其进行分析，分析其频次直方图、频率分布图，并与理论概率密度进行比较。

二、解决思路

（1）生成随机变量。使用makedist()函数创建一个概率分布对象，在此基础上，使用random()函数生成随机变量。
（2）绘制直方图。histogram()函数被使用来绘制频次分布图。
（3）将直方图的频次分布转换为频率分布图。频次除以观测次数得到区间频率，再除以区间长度即可得到频率分布图。
（4）使用pdf()函数绘制理论的概率密度函数。

三、实验代码

close all;clc;clear all;%% 参数设置SigLength = 5e7; % 信号长度% 稳定分布噪声参数
alpha = 1.5;
beta = 0;
gamma = 1;
miu = 0;%% 信号生成pd1 = makedist('Stable','alpha',alpha,'beta',beta,'gam',gamma,'delta',miu); % 产生对称α稳定分布
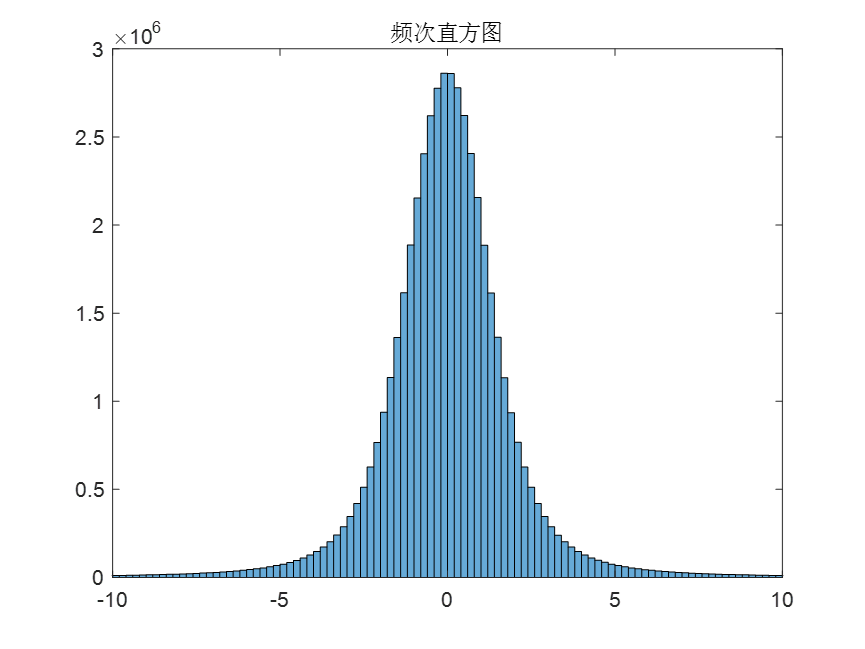
noise = random(pd1,[SigLength,1]); % 依据对象生成随机变量% noise2 = random('Stable',alpha,beta,gamma,miu,[SigLength,1]); % 方法二%% 统计直方图h1 = histogram(noise); % 作出直方图，其中BinEdges是横坐标，Values是出现次数（频数）
title('频次直方图');
xlim([-10,10]);
% hold on;nbins = h1.NumBins; % 获取直方图的分组数
x1 = zeros(nbins,1); % 将histogram估计的结果转换为频率图（将频次图转换为频率图）
for ii = 1:nbinsx1(ii,1) = transpose(0.5*(h1.BinEdges(ii) + h1.BinEdges(ii+1))); % 取区间中点
end
IntervalLength = h1.BinEdges(nbins) - h1.BinEdges(1); % 数据区间总长度
IntervalPerLength = IntervalLength/nbins; % 每个区间长度
z1 = transpose(h1.Values/SigLength/IntervalPerLength); % 重点，这是由频次直方图画概率密度的近似%% 计算理论PDFpdf1 = pdf(pd1,x1);%% 作图figure;
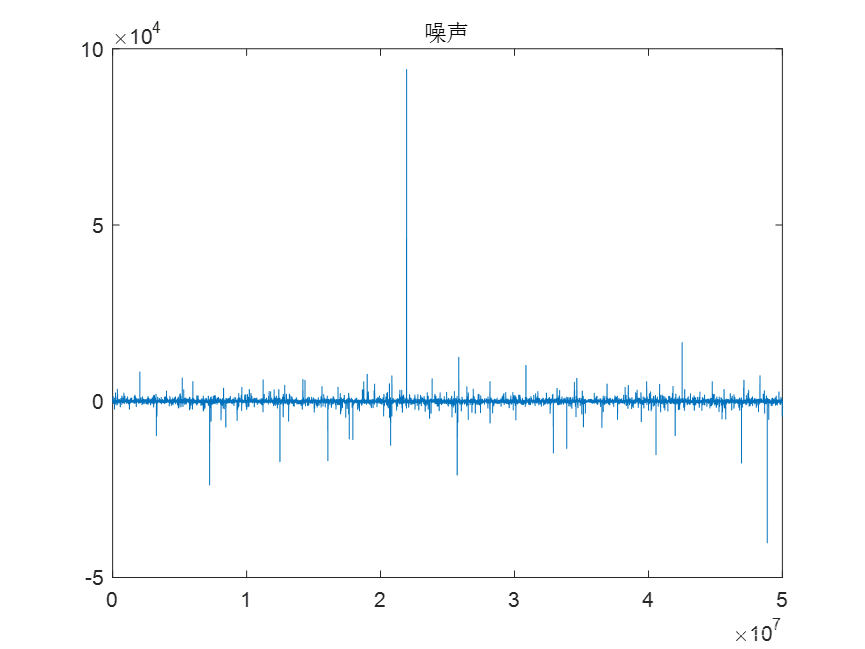
plot(noise);
title('噪声');figure;
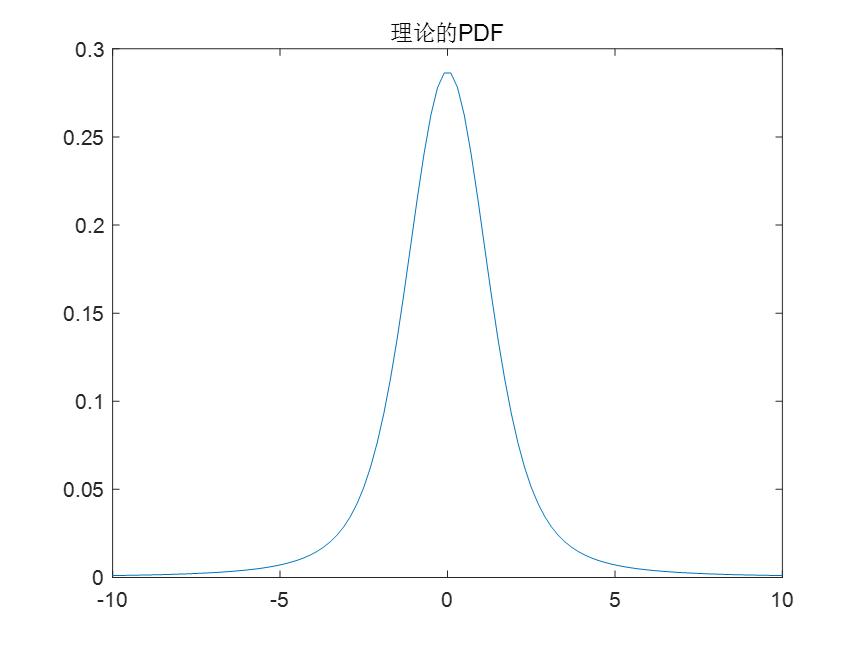
plot(x1,pdf1);
title('理论的PDF');
xlim([-10,10]);figure;
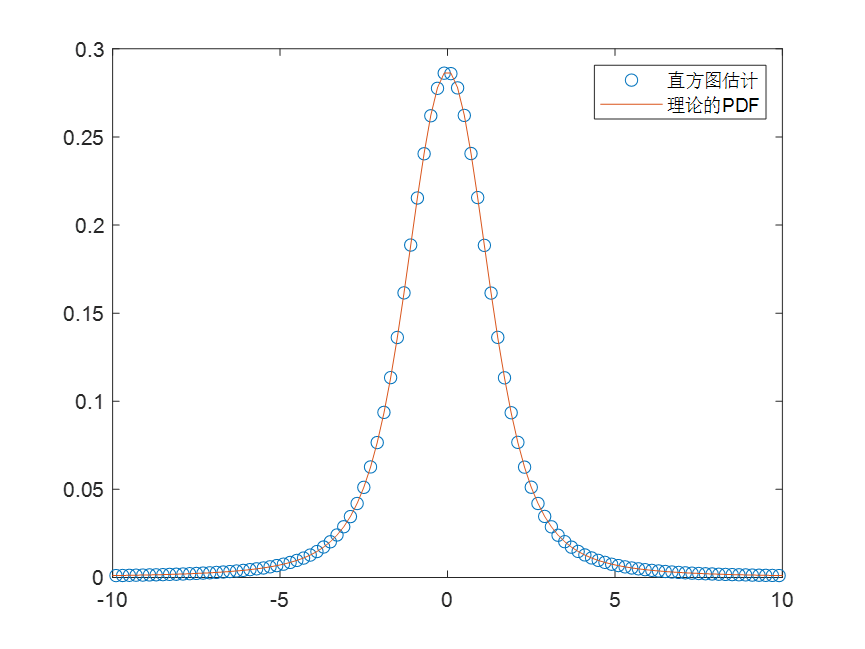
plot(x1,z1,'o');hold on;
plot(x1,pdf1);hold on;
xlim([-10,10]);
legend('直方图估计','理论的PDF');

四、实验结果