Simulink是MATLAB的重要组成部分,可以非常容易地实现可视化建模,并把理论研究和工程实践有机地结合在一起,不需要书写大量程序,只需要使用鼠标和键盘对已有模块进行简单的操作和设置。
21.1 Simulink简介
Simulink是MATLAB软件的扩展,它提供了集动态系统建模、仿真和综合分析于一体的图形用户环境,是实现动态系统建模和仿真的一个软件包。它与MATLAB的主要区别在于,其与用户的交互接口是基于Windows的模型化图形输入,其结果是用户可以把更多的精力投入到系统模型的构建,而非语言的编程上。
Simulink 提供了大量的系统模块,包括信号、运算、显示和系统等多方面的功能,可以创建各种类型的仿真系统,实现丰富的仿真功能。用户也可以定义自己的模块,进一步扩展模型的范围和功能,以满足不同的需求。为了创建大型系统,Simulink 提供了系统分层排列的功能的设计,在Simulink中可以将系统分为从高级到低级的几个层次,每层又可以细分几个部分,每层系统构建完成后,将各层连接起来构成一个完整的系统。模型创建完成之后,可以启动系统的仿真功能分析系统的动态特性,Simulink内置的分析工具包括各种仿真算法、系统线性化、寻求平衡点等,仿真结果可以以图形的方式显示在示波器窗口,以便于用户观察系统的输出结果;Simulink也可以将输出结果以变量的形式保存起来,并输入到MATLAB工作空间中以完成进一步的分析。
Simulink 可以支持多采样频率系统,即不同的系统能够以不同的采样频率进行组合,可以仿真较大、较复杂的系统
1.图形化模型与数学模型间的关系
现实中每个系统都有输入、输出和状态3个基本要素,它们之间随时间变化的数学函数关系即数学模型。图形化模型也体现了输入、输出和状态随时间变化的某种关系。只要这两种关系在数学上是等价的,就可以用图形化模型代替数学模型。
2.图形化模型的仿真过程
Simulink的仿真过程包括以下几个阶段。
(1)模型编译阶段
Simulink 引擎调用模型编译器,将模型翻译成可执行文件。其中编译器主要完成以下任务。
→计算模块参数的表达式,以确定它们的值。
→ 确定信号属性(如名称、数据类型等)。
→传递信号属性,以确定未定义信号的属性。
→优化模块。
→展开模型的继承关系(如子系统)。
→确定模块运行的优先级。
→确定模块的采样时间。
(2)连接阶段
Simulink 引擎按执行次序创建运行列表,初始化每个模块的运行信息。
(3)仿真阶段
Simulink 引擎从仿真的开始到结束,在每一个采样点按运行列表计算各模块的状态和输出。该阶段又分成以下两个子阶段。
→初始化阶段:该阶段只运行一次,用于初始化系统的状态和输出。
→迭代阶段:该阶段在定义的时间段内按采样点间的步长重复运行,并将每次的运算结果用于更新模型。在仿真结束时获得最终的输入、输出和状态值。
21.1.1 Simulink模型的特点
(1)仿真结果的可视化
(2)模型的层次性
(3)可封装子系统
21.1.2 Simulink模型的数据类型
Simulink在仿真开始之前和运行过程中会自动确认模型的类型安全性,以确保该模型产生的代码不会上溢或者下溢。
1. Simulink支持的数据类型
Simulink支持所有的MATLAB内置的数据类型,除此之外,Simulink还支持布尔类型,绝大多数模块都默认double类型的数据,但有些模块需要布尔类型和复数类型。
2. 数据类型的统一
若模块的输入输出支持的数据类型不相同,则在仿真时会弹出错误提示对话框,告知冲突的信号和端口,此时可以尝试在冲突的模块间插入DataTypeConversion(数据类型转换)模块来解决。示例如下:
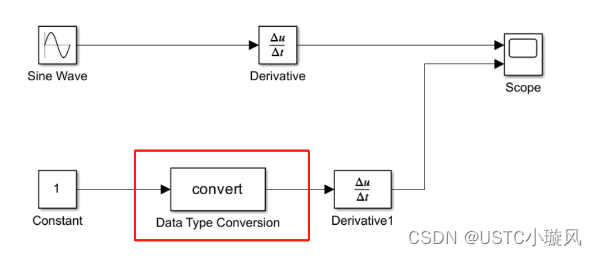
3. 复数类型
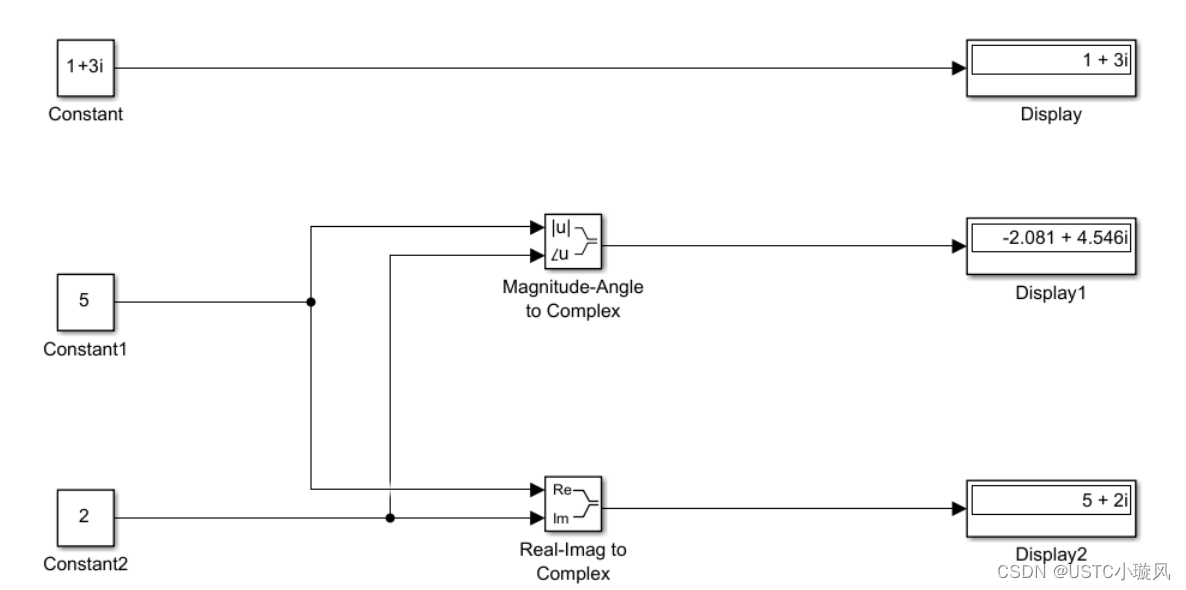
Simulink默认的信号值都是复数,但在实际问题中需要处理复数信号。在Simulink中通常用Real-Image to Complex模块和Magnitude-Angle to Complex模块来建立处理复数信号的模型。如下图示例所示:
21.2 Simulink模块库
21.2.1 常用模块库
1.Commonly Used Blocks库(常用模块库)
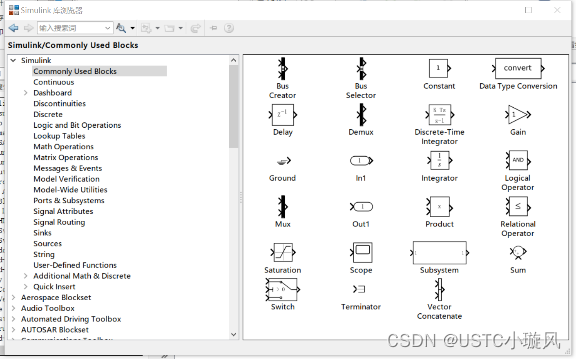
| 模块名 | 功能 |
| Bus Creator | 将输入信号合并成向量信号 |
| Bus Selector | 将输入向量分解成多个信号,输入只接收从Mux和BusCreator输出的信号 |
| Constant | 输出常量信号 |
| Data Type Conversion | 数据类型的转换 |
| DemuX | 将输入向量转换成标量或更小的标量 |
| Discrete-Time lntegrator | 离散积分器模块 |
| Gain | 增益模块 |
| In1 | 输入模块 |
| Integrator | 连续积分模块 |
| Logical Operator | 逻辑运算模块 |
| Mux | 将输入的向量、标量或矩阵信号合成 |
| Out1 | 输出模块 |
| Product | 乘法器,执行标量、向量或矩阵的乘法 |
| Relational Operator | 关系运算,输出布尔类型数据 |
| Saturation | 定义输入信号的最大值和最小值 |
| Scope | 在示波器中输出 |
| Subsystem | 创建子系统 |
| Sum | 加法器 |
| Switch | 选择器,根据第二个输入信号来选择输出第一个信号还是第三个信号 |
| Terrainator | 终止输出,用于防止模型最后的输出端没有接任何模块时报错 |
| Unit Delay | 单位时间延迟 |
2. Continuous库(连续系统库)

| 模块名 | 功能 |
| Derivative | 数值微分 |
| Integrator | 积分器与 Commonly Used Blocks 子库中的同名模块一样 |
| State-Space | 创建状态空间模型 dx/dt= Ax + Bu y= Cx+ Du |
| Transport Delay | 定义传输延迟,如果将延迟设置得比仿真步长大,就可以得到更精确的结果 |
| Transfer Fen | 用矩阵形式描述的传输函数形 |
| Variable Transport Delay | 定义传输延迟,第一个输入接收输入,第二个输入接收延迟时间用 |
| Zero-Pole | 矩阵描述系统零点,用向量描述系统极点和增益 |
21.2.2 子系统及其封装
若模型的结构过于复杂,则需要将功能相关的模块组合在一起形成几个小系统,即子系统,后在这些子系统之间建立连接关系,从而完成整个模块的设计。这种设计方法实现了模型图表的次化,使整个模型变得非常简洁,使用起来非常方便。
用户可以把一个完整的系统按照功能划分为若干个子系统,而每个子系统又可以进一步划分为更小的子系统,由此可以将系统分为多层。
1. 子系统的创建方法
(1)通过子系统模块来创建子系统;
(2)组合已经存在的模块集
2. 封装子系统
21.3 模块的创建
模块是Simulink建模的基本元素,了解各模块的作用是熟练掌握Simulink的基础。下面介绍利用Simulink进行系统建模和仿真的基本步骤。
(1)绘制系统流程图。首先将所要建模的系统根据功能划分为若干子系统,然后用模块来搭建每个子系统;
(2)启动Simulink模块库浏览器,建立一个空白模型窗口;
(3)将所需模块放入空白模型窗口中,将系统流程图的布局连接各模块,并封装子系统;
(4)设置各模块的参数以及仿真有关的各种参数;
(5)保存模型,模型文件的后缀名为.mdl;
(6)运行并调试模型
21.3.1 创建模块文件
21.3.2 模块的基本操作
1. 模块的选择
2. 模块的放置
3. 模块的位置调整
4. 模块的属性编辑
21.3.3 模块参数设置
1. 参数设置
2. 属性设置
示例1:滤波信号输出
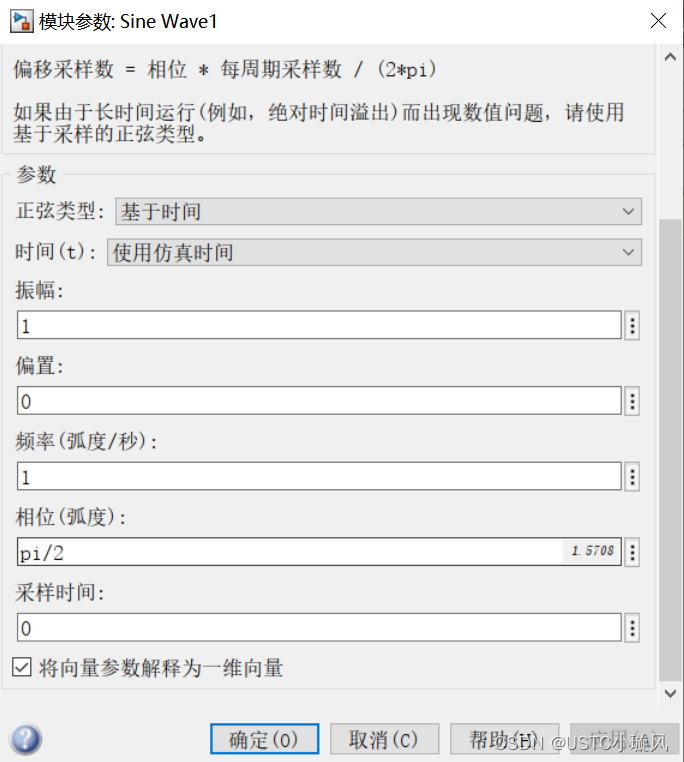
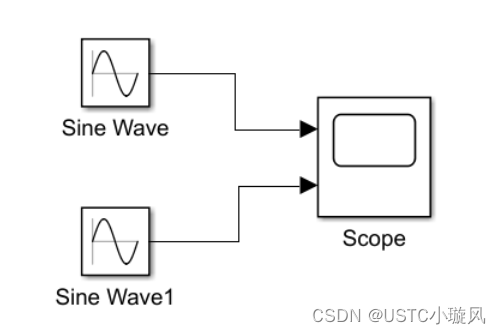

示例2:正弦信号输出


21.3.4 模块的连接
1. 直线的连接
2. 直线的编辑
示例1:正弦信号的最大值、最小值输出

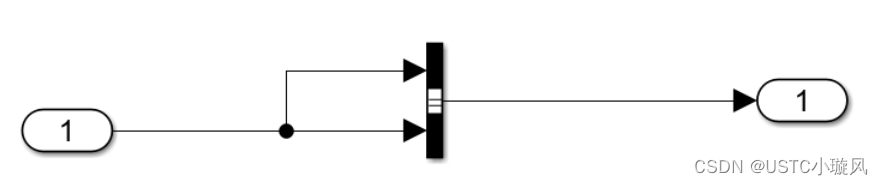
示例2:信号输出


21.4 仿真分析
21.4.1 仿真参数设置
(1)Solver(求解器)面板
主要用于设置仿真开始和结束的时间,选择解法器并设置相应的参数。
(2)Data Import/Export(输入/输出数据)面板
21.4.2 仿真的运行和分析
1. 仿真结果输出分析
(1)在模型中将信号输入Scope(示波器)模块或XY Graph模型;
(2)将输出写入To Workspace模块,然后使用MATLAB绘图功能;
(3)将输出写入To File模块,然后使用MATLAB文件读取和绘图功能。
2. 线性化分析
3. 平衡点分析
21.4.3 仿真错误分析
21.5 回调函数
21.6 S函数
S函数(System 函数)是一种描述动态系统的计算机语言,可以用MATLAB、C、C++、Ada和 FORTRAN 语言编写。用mex 命令可将C、C++等语言编写的S函数编译成 MEX文件,从而可以像 MATLAB 中的其他 MEX文件一样,动态地连接到MATLAB。S函数采用一种特殊的调用语法和 Simulink 解法器进行交互,这种交互与解法器和 Simulink 自带模块间的交互十分类似。S函数可以用来描述连续、离散和混杂系统。
S函数是扩展Simulink 功能的强有力的工具,可以实现以下操作:
(1)用多种语言来创建新的通用性的 Simulink 模块;
(2)可以在 User-Defined Functions 模块库的 S-function 模块中通过名称来调用并封装;
(3)将一个系统描述成一个数学方程;
(4)便于图形化仿真;
(5)可以创建代表硬件驱动的模块。
21.7 综合实例——轴系扭转振动仿真
某柴油机4级系统振动方程:其中,
轴系各质量点扭振转角位移;轴系节点向量
;轴系转动惯量
,阻尼
,刚度矩阵
。当
时,计算系统自由振动;当
,计算系统受迫振动。
系统受迫振动微分方程表述为,将原微分方程修改为


转化方程组:对于系统受迫振动微分方程 ,
,转化为高阶微分方程,这里需要将其转换为一阶微分方程组即状态方程,然后使用函数ode45()进行求解。令
,则状态方程为
![]()
创建函数文件verderpol.m:
function [xn]=verderpol(t,x)
global mu
xn=[x(2);0.2*mu-400*x(1)-2600*x(2)];
end
在命令行窗口中输入下面的程序:
>> global mu;
>> mu=1200;
>> y0=[1200;0];
>> [t,x]=ode45(@verderpol,[0,1200],y0);
>> subplot(1,2,1);plot(t,x);
>> title('时间响应曲线')
>> xlim([-200,1500])
>> subplot(1,2,2);plot(x(:,1),x(:,2))
>> title('平面曲线')
>> xlim([0,1500])
结果:
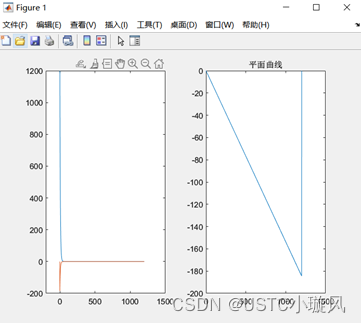
参考资料:
[1] 天工在线. MATLAB2020从入门到精通·实战案例版[M]. 北京: 中国水利水电出版社, 2020.