一、什么是岭回归

其实岭回归就是带L2正则化的线性回归

岭回归，其实也是一种线性回归。只不过在算法建立回归方程时候，加上L2正则化的限制，从而达到解决过拟合的效果

二、API

1、sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, solver="auto", normalize=False)
具有l2正则化的线性回归
alpha：正则化力度=惩罚项系数，也叫λ
    λ取值：0~1或1~10
fit_intercept：是否添加偏置
solver：会根据数据自动选择优化方法
    sag：如果数据集、特征都比较大，会自动选择sag这个随机梯度下降优化
normalize：数据是否进行标准化
    normalize=False：可以在fit之前调用preprocessing.StandardScaler标准化数据
    normalize=True：在预估器流程前会自动做标准化
Ridge.coef_：回归权重
Ridge.intercept_：回归偏置

2、Ridge方法相当于SGDRegressor(penalty='l2', loss="squared_loss")，只不过SGDRegressor实现了一个普通的随机梯度下降学习，推荐使用Ridge(实现了SAG)
penalty：可以是l1或l2，这里是给线性回归加上L2惩罚项

3、sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)
加上了交叉验证的岭回归
具有l2正则化的线性回归，可以进行交叉验证
coef_：回归系数

三、正则化力度（惩罚项系数）对最终结果有什么影响

1、惩罚项系数是上面的λ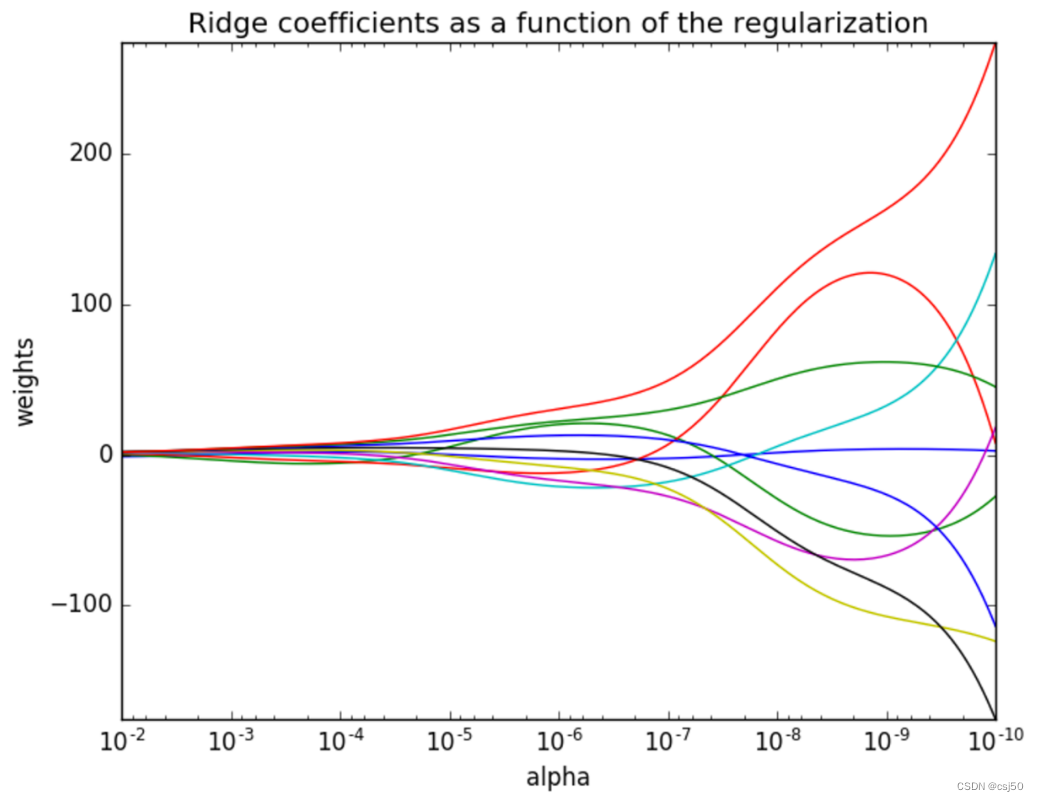

横坐标是正则化力度，也就是alpha。纵坐标是权重系数

正则化力度越大（向左），权重系数会越小（接近于0）
正则化力度越小（向右），权重系数会越大

四、波士顿房价预测

1、修改day03_machine_learning.py

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.metrics import mean_squared_errordef linear1():"""正规方程的优化方法对波士顿房价进行预测"""# 1、获取数据boston = load_boston()# 2、划分数据集x_train,x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=10)# 3、标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# 4、预估器estimator = LinearRegression()estimator.fit(x_train, y_train)# 5、得出模型print("正规方程-权重系数为：\n", estimator.coef_)print("正规方程-偏置为：\n", estimator.intercept_)# 6、模型评估y_predict = estimator.predict(x_test)print("预测房价：\n", y_predict)error = mean_squared_error(y_test, y_predict)print("正规方程-均方误差为：\n", error)return Nonedef linear2():"""梯度下降的优化方法对波士顿房价进行预测"""# 1、获取数据boston = load_boston()# 2、划分数据集x_train,x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=10)# 3、标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# 4、预估器estimator = SGDRegressor()estimator.fit(x_train, y_train)# 5、得出模型print("梯度下降-权重系数为：\n", estimator.coef_)print("梯度下降-偏置为：\n", estimator.intercept_)# 6、模型评估y_predict = estimator.predict(x_test)print("预测房价：\n", y_predict)error = mean_squared_error(y_test, y_predict)print("梯度下降-均方误差为：\n", error)return Nonedef linear3():"""岭回归对波士顿房价进行预测"""# 1、获取数据boston = load_boston()# 2、划分数据集x_train,x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=10)# 3、标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# 4、预估器estimator = Ridge()estimator.fit(x_train, y_train)# 5、得出模型print("岭回归-权重系数为：\n", estimator.coef_)print("岭回归-偏置为：\n", estimator.intercept_)# 6、模型评估y_predict = estimator.predict(x_test)print("预测房价：\n", y_predict)error = mean_squared_error(y_test, y_predict)print("岭回归-均方误差为：\n", error)return Noneif __name__ == "__main__":# 代码1：正规方程的优化方法对波士顿房价进行预测linear1()# 代码2：梯度下降的优化方法对波士顿房价进行预测linear2()# 代码3：岭回归对波士顿房价进行预测linear3()

2、运行结果

正规方程-权重系数为：[-1.16537843  1.38465289 -0.11434012  0.30184283 -1.80888677  2.341711660.32381052 -3.12165806  2.61116292 -2.10444862 -1.80820193  1.19593811-3.81445728]
正规方程-偏置为：21.93377308707127
预测房价：[31.11439635 31.82060232 30.55620556 22.44042081 18.80398782 16.2762532236.13534369 14.62463338 24.56196194 37.27961695 21.29108382 30.6125824127.94888799 33.80697059 33.25072336 40.77177784 24.3173198  23.2977324125.50732006 21.08959787 32.79810915 17.7713081  25.36693209 25.0381105932.51925813 20.4761305  19.69609206 16.93696274 38.25660623  0.7015249932.34837791 32.21000333 25.78226319 23.95722044 20.51116476 19.537272583.87253095 34.74724529 26.92200788 27.63770031 34.47281616 29.8051127118.34867051 31.37976427 18.14935849 28.22386149 19.25418441 21.7149039538.26297011 16.44688057 24.60894426 19.48346848 24.49571194 34.4891563526.66802508 34.83940131 20.91913534 19.60460332 18.52442576 25.0017879919.86388846 23.46800342 39.56482623 42.95337289 30.34352231 16.893355923.88883179  3.33024647 31.45069577 29.07022919 18.42067822 27.4431489719.55119898 24.73011317 24.95642414 10.36029002 39.21517151  8.3074326218.44876989 30.31317974 22.97029822 21.0205003  19.99376338 28.647549730.88848414 28.14940191 26.57861905 31.48800196 22.25923033 -5.3597325221.66621648 19.87813555 25.12178903 23.51625356 19.23810222 19.046423427.32772709 21.92881244 26.69673066 23.25557504 23.99768158 19.2845825921.19223276 10.81102345 13.92128907 20.8630077  23.40446936 13.9168948428.87063386 15.44225147 15.60748235 22.23483962 26.57538077 28.6420362324.16653911 18.40152087 15.94542775 17.42324084 15.6543375  21.0413626433.21787487 30.18724256 20.92809799 13.65283665 16.19202962 29.2515560313.28333127]
正规方程-均方误差为：32.44253669600673
梯度下降-权重系数为：[-1.10819189  1.24846017 -0.33692976  0.35488997 -1.5988338   2.497786120.23532503 -2.95918503  1.78713201 -1.30658932 -1.7651645   1.22848984-3.78378732]
梯度下降-偏置为：[21.9372382]
预测房价：[30.55704932 32.05173832 30.60725341 23.44937757 18.99917813 16.1000257536.35984687 14.8219597  24.40027383 37.32474782 21.5136228  30.6786441827.64263953 33.58715018 33.34357549 41.02961052 24.56190835 22.826545725.55091571 21.70092286 32.87467814 17.66098552 25.68694993 25.1525498533.16850623 20.32656198 19.71924549 16.85013083 38.36906677 -0.063612532.73406521 32.08051235 26.11082213 24.04506778 20.25729015 19.777164693.70619504 34.45691833 26.92882569 27.80690875 34.66542721 29.5705631918.17563119 31.52879095 17.99350098 28.56441014 19.19066091 21.4221363238.1145129  16.56749119 24.53862046 19.30611604 24.18857419 35.0850191926.86672187 34.85386528 21.23005703 19.56549835 18.32581965 25.0223145420.21024376 23.85118373 40.23475025 43.25772524 30.50012791 17.1749763623.97539731  2.78651333 31.14016986 29.84080487 18.33899648 27.4617082719.28192918 24.53788739 25.36787612 10.25023757 39.41179243  7.9710262818.11455433 30.92992358 22.98914795 21.89678026 20.29065302 28.5543570831.1738028  28.36545081 26.50764708 31.89860003 22.31334327 -5.7728714921.72210665 19.74247295 25.14530383 23.69494522 18.83967629 19.1579255427.3208327  22.03369451 26.56809141 23.54003515 23.94824339 19.4946140121.04641077  9.8365073  13.99736749 21.15777556 23.16210392 15.1980546828.94748286 15.82614487 15.49056654 21.98524785 27.04398453 28.7181679624.00103595 18.26483509 15.80645364 17.68948585 15.8560435  20.7547522933.18483916 30.80830718 21.1511169  14.13781488 16.30748901 29.1982781413.02414535]
梯度下降-均方误差为：32.589364375873274
岭回归-权重系数为：[-1.15338693  1.36377246 -0.13566076  0.30685046 -1.77429221  2.35657730.31109246 -3.08360389  2.51865451 -2.02086382 -1.79863992  1.19474755-3.79397362]
岭回归-偏置为：21.93377308707127
预测房价：[31.02182904 31.81762296 30.5307756  22.56101986 18.83367243 16.2772061636.11020039 14.65795076 24.53401701 37.23901719 21.30179513 30.5929445527.88884922 33.74220094 33.22724169 40.75065038 24.34249271 23.2334033225.49591227 21.16642876 32.76426793 17.77262939 25.375461   25.0421619732.55916012 20.46991441 19.71767638 16.94589789 38.22924617  0.6794581532.36570422 32.16246666 25.81396987 23.96859847 20.48378122 19.562226923.92363179 34.6745904  26.8972682  27.62853379 34.46087333 29.7505016518.3389973  31.36674393 18.1533717  28.23955372 19.25477732 21.6743993838.20456951 16.47703009 24.58448733 19.46850857 24.45078345 34.5144544526.66775912 34.80353844 20.94272686 19.60603364 18.50096422 24.9938738619.89923157 23.49308585 39.58682259 42.93017524 30.32881249 16.930963123.89113672  3.3223193  31.37851848 29.1623479  18.42211411 27.4382901119.52539153 24.68355681 24.98105953 10.39357796 39.19016669  8.3112177518.43234108 30.3568052  22.97522145 21.12688558 20.03476147 28.6193767930.88518359 28.14590934 26.56509999 31.51187089 22.27686749 -5.3124194821.68661135 19.86726981 25.1163169  23.53556822 19.21105599 19.0843777227.30869525 21.94344682 26.65541972 23.26883666 23.9958039  19.3060780621.18985411 10.71242971 13.95709927 20.89648522 23.36054449 14.0580326528.85147775 15.51591674 15.61567092 22.20129229 26.6018834  28.6319077524.13317802 18.39685365 15.94882155 17.46607437 15.7003571  21.004634133.16362767 30.23909552 20.94330259 13.73934571 16.22231382 29.2129078713.28412904]
岭回归-均方误差为：32.4536692771621