目录
1.二叉搜索树
1.1二叉搜索树的介绍
1.2.二叉搜索树的实现
1.2.1二叉搜索树的创建
1.2.2查找关键字
1.2.3插入
1.2.4删除
1.3二叉搜索树的性能分析
2.Map
Map官方文档
2.1Map 的常用方法说明
2.2关于Map.Entry的说明,>
2.3注意事项
2.4reeMap和HashMap的区别
3.Set
3.1常见方法说明
3.2注意事项
3.3TreeSet和HashSet的区别
1.二叉搜索树
1.1二叉搜索树的介绍
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树 :
（1）若它的左子树不为空，则左子树上所有节点的值都小于根节点的值（2）若它的右子树不为空，则右子树上所有节点的值都大于根节点的值（3）它的左右子树也分别为二叉搜索树
比如以下：
int[] array ={5,3,4,1,7,8,2,6,0,9};
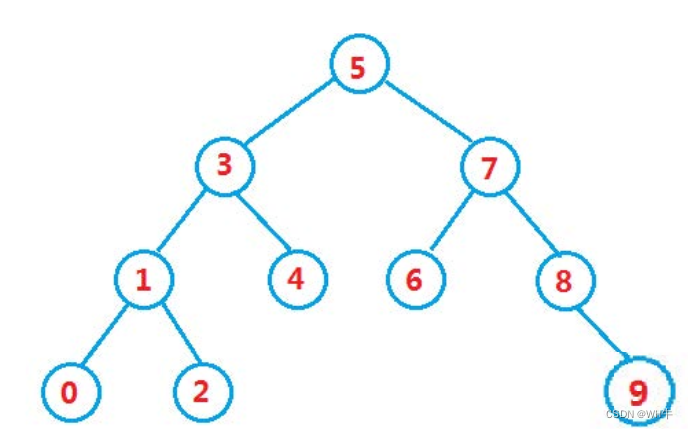
1.2.二叉搜索树的实现
1.2.1二叉搜索树的创建
public class BinarySearchTree {class TreeNode {public int val ;public TreeNode left;public TreeNode right;public TreeNode(int val) {this.val = val;}}public TreeNode root;//根节点
}1.2.2查找关键字
步骤：
若根节点不为空：
- 如果根节点key==查找key，返回true
- 如果根节点key > 查找key，在其左子树查找
- 如果根节点key < 查找key，在其右子树查找
找不到，返回false
代码：
public boolean search(int key) {TreeNode cur = root;while (cur != null) {if (cur.val ==key){return true;} else if (cur.val>key) {cur=cur.left;}else{cur=cur.right;}}return false;}1.2.3插入
插入操作可以分为以下两种情况：
（1）如果树为空树，即根 == null，直接插入
（2）如果树不是空树，按照查找逻辑确定插入位置，插入新结点
那怎么找合适位置呢？
- 如果节点root.val==val，该值在搜索数中已经存在，无需插入，return flase;
- 如果节点root.val>val，在其左子树找合适位置
- 如果节点root.val<val，在其右子树找合适位置
代码：
public boolean insert(int val) {TreeNode treeNode = new TreeNode(val);if (root == null) {root=treeNode;return true;}TreeNode cur=root;TreeNode parent = null;while(cur!=null){if (cur.val == val) {return false;} else if (cur.val > val) {parent=cur;cur = cur.left;} else {parent=cur;cur = cur.right;}}if(parent.val>val){parent.left=treeNode;}else {parent.right=treeNode;}return true;}1.2.4删除
设待删除结点为 cur, 待删除结点的双亲结点为 parent
1. cur.left == null
（1） cur 是 root ，则 root = cur.right
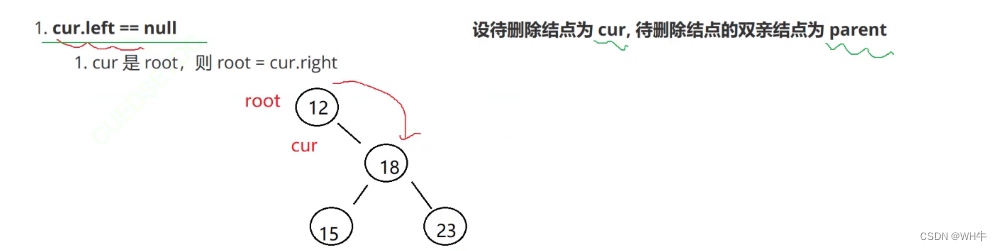
（2） cur 不是 root，cur 是 parent.left，则 parent.left = cur.right
（3） cur 不是 root，cur 是 parent.right，则 parent.right = cur.right
2. cur.right == null
（1） cur 是 root ，则 root = cur.left
（2） cur 不是 root ， cur 是 parent.left ，则 parent.left = cur.left
（3） cur 不是 root ， cur 是 parent.right ，则 parent.right = cur.left
这里与1. cur.left == null大同小异不做过多解释
3. cur.left != null && cur.right != null
步骤：
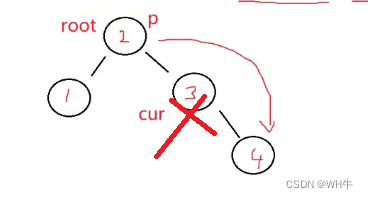
我们使用target来遍历寻找子树中关键节点，targetParent用来记录target的父亲节点
找到相应节点后与待删除的cur节点的值进行替换，最后删除target结点即可
例子：
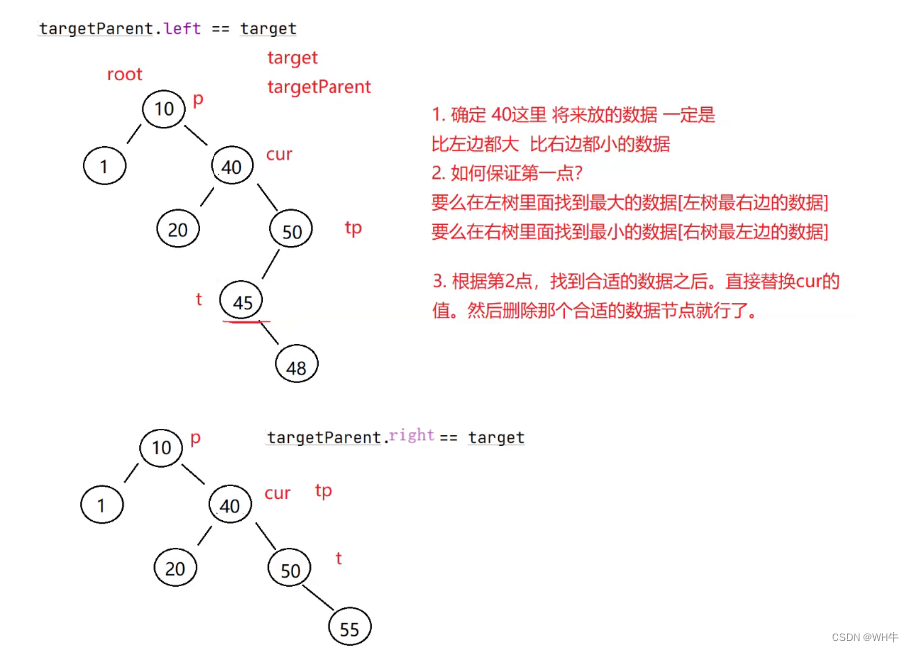
代码：
public void remove(int val) {TreeNode cur = root;TreeNode parent = null;while (cur != null) {if (val == cur.val) {removeNode(parent, cur);break;} else if (val < cur.val) {parent = cur;cur = cur.left;} else {parent = cur;cur = cur.right;}}}private void removeNode(TreeNode parent, TreeNode cur) {if (cur.left==null){if(cur==root){root=cur.right;}else if(parent.left==cur){parent.left=cur.right;}else{parent.right=cur.right;}} else if (cur.right==null) {if(cur==root){root=cur.left;}else if(parent.left==cur){parent.left=cur.left;}else{parent.right=cur.left;}}else{TreeNode target = cur.right;TreeNode targetParent = cur;while(target.left!=null){targetParent = target;target = target.left;}if(targetParent.left==target){targetParent.left=target.right;}else{targetParent.right=target.right;}}}1.3二叉搜索树的性能分析
插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。对有 n 个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度 的函数，即结点越深，则比较次数越多。但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：
但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：
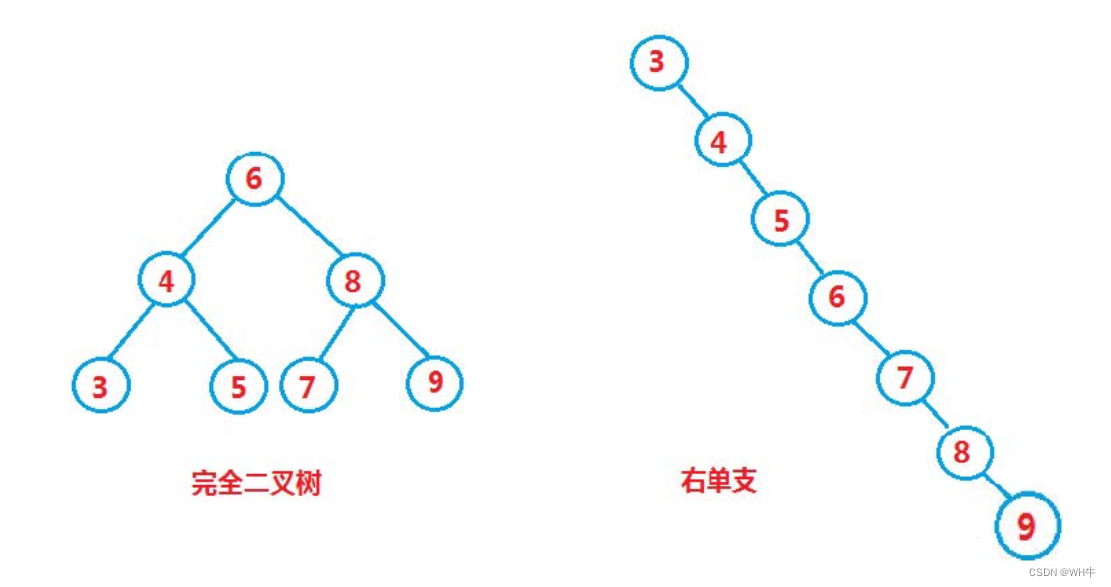
2.Map
Map官方文档
Map 是一个接口类，该类没有继承自 Collection ，该类中存储的是 <K,V> 结构的键值对，并且 K 一定是唯一的，不 能重复 。
2.1Map 的常用方法说明
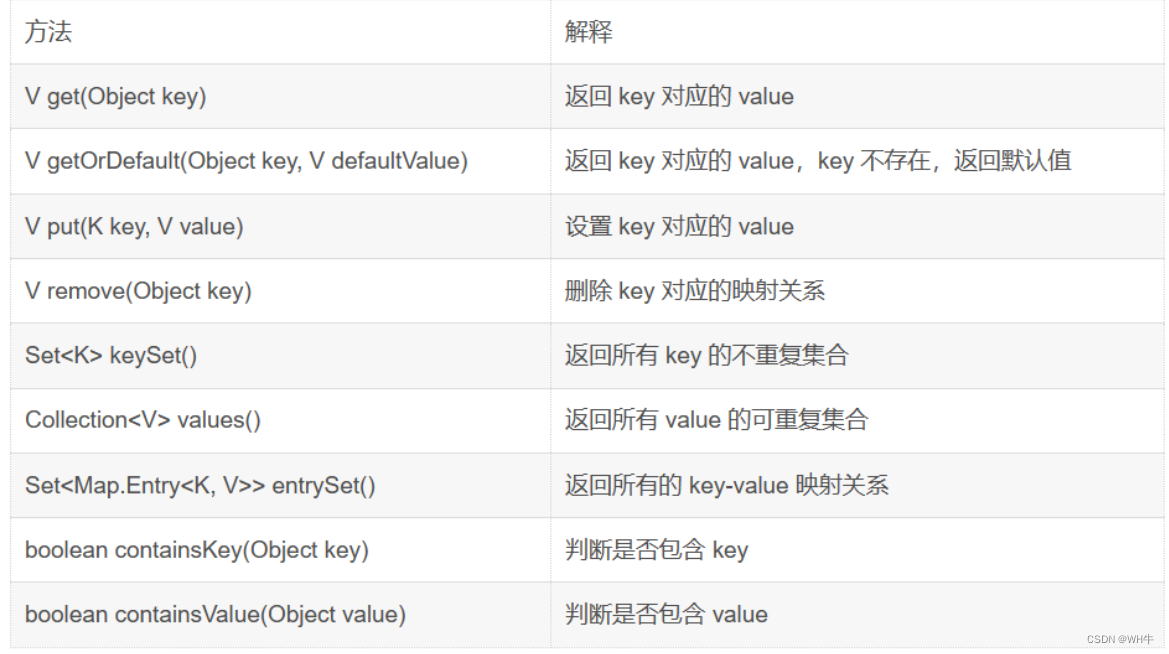
举例部分方法：
public class TestMap {public static void main(String[] args) {Map<String,Integer> map=new TreeMap<>();map.put("wang",1);map.put("zhang",3);map.put("li",5);System.out.println(map);//{li=5, wang=1, zhang=3}// GetOrDefault(): 如果key存在，返回与key所对应的value，如果key不存在，返回一个默认值System.out.println(map.getOrDefault("wang",0));//1System.out.println(map.getOrDefault("abcdef",0));//0// 返回所有 key 的不重复集合Set keys=map.keySet();System.out.println(keys);//[li, wang, zhang]//返回所有 value 的可重复集合Collection vals= map.values();System.out.println(vals);//[5, 1, 3]// 打印所有的键值对// entrySet(): 将Map中的键值对放在Set中返回了for(Map.Entry<String, Integer> entry : map.entrySet()){System.out.println(entry.getKey() + "--->" + entry.getValue());}//li--->5//wang--->1//zhang--->3}}
2.2关于Map.Entry<K, V>的说明
Map.Entry<K, V> 是 Map 内部实现的用来存放 <key, value> 键值对映射关系的内部类 ，该内部类中主要提供了 <key, value>的获取， value 的设置以及 Key 的比较方式。
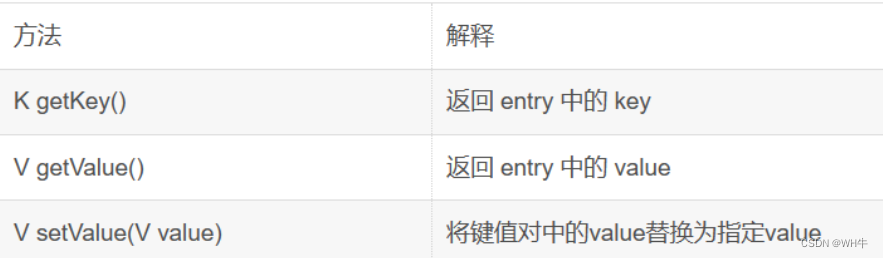
注意：Map.Entry<K,V>并没有提供设置Key的方法
2.3注意事项
1. Map 是一个接口，不能直接实例化对象 ，如果 要实例化对象只能实例化其实现类 TreeMap 或者 HashMap2. Map 中存放键值对的 Key 是唯一的， value 是可以重复的3. 在 TreeMap 中插入键值对时， key 不能为空，否则就会抛 NullPointerException 异常 ， value 可以为空。但 是HashMap 的 key 和 value 都可以为空。4. Map 中的 Key 可以全部分离出来，存储到 Set 中 来进行访问 ( 因为 Key 不能重复 )5. Map 中的 value 可以全部分离出来，存储在 Collection 的任何一个子集合中 (value 可能有重复 ) 。6. Map 中键值对的 Key 不能直接修改， value 可以修改，如果要修改 key ，只能先将该 key 删除掉，然后再来进行 重新插入。
2.4reeMap和HashMap的区别
3.Set
Set官方文档
Set与Map主要的不同有两点：Set是继承自Collection的接口类，Set中只存储了Key。
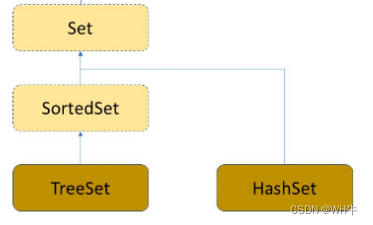
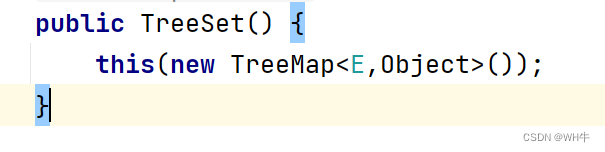
set的底层是map
3.1常见方法说明
举例部分方法：
public class TextSet {public static void main(String[] args) {Set<String> set=new TreeSet<>();// add(key): 如果key不存在，则插入，返回ture// 如果key存在，返回falseset.add("wang");set.add("hang");set.add("li");Iterator<String> it=set.iterator();while(it.hasNext()){System.out.println(it.next());}//hang//li//wang}
}
3.2注意事项
1. Set 是继承自 Collection 的一个接口类2. Set 中只存储了 key ，并且要求 key 一定要唯一3. TreeSet 的底层是使用 Map 来实现的，其使用 key 与 Object 的一个默认对象作为键值对插入到 Map 中的4. Set 最大的功能就是对集合中的元素进行去重5. 实现 Set 接口的常用类有 TreeSet 和 HashSet ，还有一个 LinkedHashSet ， LinkedHashSet 是在 HashSet 的基础 上维护了一个双向链表来记录元素的插入次序。6. Set 中的 Key 不能修改，如果要修改，先将原来的删除掉，然后再重新插入7. TreeSet 中不能插入 null 的 key ， HashSet 可以。
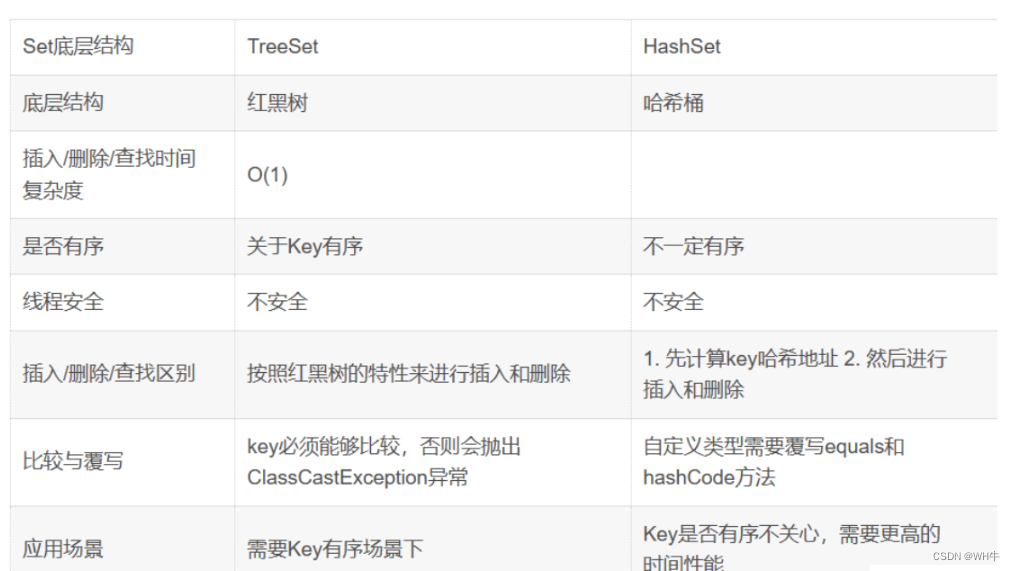
3.3TreeSet和HashSet的区别
以上为我个人的小分享，如有问题，欢迎讨论！！！
都看到这了，不如关注一下，给个免费的赞 
