目录

1.原理介绍

1.1 有限差分法介绍

1.2 有限差分法步骤

2.案例分析

2.1 问题重述

2.2 问题求解

---

1.原理介绍

1.1 有限差分法介绍

有限差分法是一种常用的数值计算方法，用于求解偏微分方程或常微分方程的数值解。它的基本思想是将连续的空间区域离散化为有限个离散点，在这些点上近似表示方程，并通过差分近似求解。

在有限差分法中，首先将连续的空间区域划分为网格，每个网格上的点称为节点。然后，通过在节点上进行近似，将偏微分方程或常微分方程转化为节点上的代数方程，进而求解得到数值解。

常用的有限差分格式包括向前差分、向后差分和中心差分等。根据所需要求解的方程类型和边界条件，选择合适的差分格式来近似方程中的导数项。

1.2 有限差分法步骤

有限差分法步骤可以概括如下：

1. 空间离散化：将连续的空间区域划分为离散的网格，每个网格点称为节点。通过确定节点的位置和间距，将方程转化为节点上的代数方程。

2. 时间离散化（对于时间相关的方程）：将连续的时间区域划分为离散的时间步长。根据时间步长和空间离散化得到的节点位置，将方程的时间导数近似为节点之间的差分。

3. 差分近似：通过将偏微分方程中的导数用有限差分方式近似，将方程转化为节点上的代数方程。常用的差分格式包括向前差分、向后差分和中心差分等。

4. 边界条件处理：根据具体问题的边界条件，在节点上设置相应的边界条件。边界条件约束了数值解在边界上的取值，可通过差分方式将边界条件转化为代数方程。

5. 求解代数方程：通过数值迭代方法，如迭代法或直接矩阵求解法，求解得到节点上的数值解。根据需要，可以使用迭代方法进行逐步迭代，或者直接构建并求解代数方程组。

6. 后处理：根据数值解，可以进行后处理分析，如计算数值解的误差、可视化数值解等。

有限差分法的核心思想是通过离散化的节点和差分近似，将偏微分方程或常微分方程转化为代数方程，从而利用计算机进行数值求解。离散化的精细程度以及差分格式的选择会对数值解的精确度和稳定性产生影响，因此需要在实际应用中进行适当的调参和验证。

2.案例分析

2.1 问题重述

有限差分法可以用来求解泊松方程，泊松方程是一种常见的二阶偏微分方程，形式为：

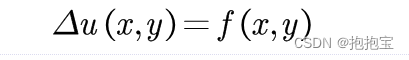
其中，△表示拉普拉斯算子，u(x, y) 是未知解函数，f(x, y) 是已知的源项函数。

为了利用有限差分法求解泊松方程，我们需要进行以下步骤：

1. 网格划分：将求解区域划分为离散的网格，每个网格点称为节点。选择合适的网格大小和节点间距，可以根据需要调整离散化的精细程度。

2. 差分近似：通过离散化的节点和差分方式，将泊松方程中的二阶导数近似为节点之间的差分。常用的差分格式包括中心差分、向前差分和向后差分等。

   对于中心差分格式，我们有如下近似：
   

   
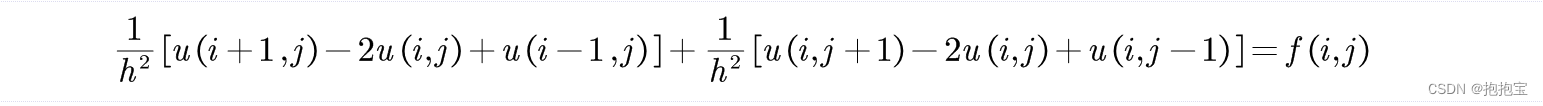
   其中，(i, j) 表示节点的坐标，u(i, j) 是节点上的解，h 是节点间距。

3. 边界条件处理：根据具体问题的边界条件，在节点上设置相应的边界条件。常见的边界条件有固定值边界条件、导数边界条件等。边界条件的设定方法基于物理问题的特性。

4. 代数方程求解：根据离散化得到的差分方程和边界条件，构建一个线性代数方程组，其中未知数是节点上的解。可以使用直接法（如高斯消元法）或迭代法（如雅可比迭代法、Gauss-Seidel 迭代法）求解方程组。

5. 后处理：根据数值解，可以进行后处理分析，如计算数值解的误差、可视化数值解等。

2.2 问题求解

利用Python实现有限差分法求解泊松方程代码如下：

import numpy as np# 定义网格尺寸
N = 10  # 网格数量
L = 1.0  # 区域长度
h = L / (N + 1)  # 网格间距# 定义源项函数
def f(x, y):return -2 * (np.pi**2) * np.sin(np.pi * x) * np.sin(np.pi * y)# 初始化节点上的解
u = np.zeros((N, N))# 设置边界条件
# 这里以固定值边界条件为例，边界上的解为0
u[0, :] = 0  # 下边界
u[N-1, :] = 0  # 上边界
u[:, 0] = 0  # 左边界
u[:, N-1] = 0  # 右边界# 迭代求解
max_iter = 1000  # 最大迭代次数
tolerance = 1e-4  # 收敛容许误差for k in range(max_iter):u_old = np.copy(u)for i in range(1, N-1):for j in range(1, N-1):u[i, j] = 0.25 * (u_old[i+1, j] + u_old[i-1, j] + u_old[i, j+1] + u_old[i, j-1] - h**2 * f(i*h, j*h))# 计算收敛误差error = np.max(np.abs(u - u_old))# 判断是否达到收敛条件if error < tolerance:break# 打印数值解
print(u)

求解结果;

绘制数值解的三维图像：

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# 绘制数值解的三维图像
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, u, cmap='coolwarm')# 设置坐标轴标签
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('u')# 显示图像
plt.show()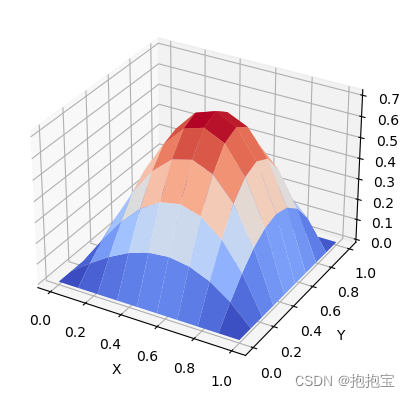

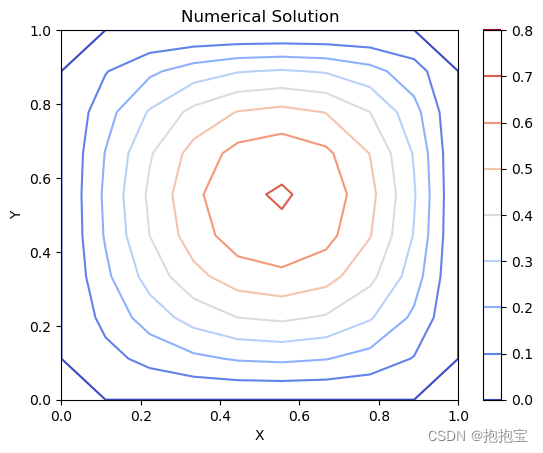
绘制数值解的二维等高线图：

# 绘制数值解的等高线图
plt.contour(X, Y, u, cmap='coolwarm')
plt.colorbar()# 标题和坐标轴标签
plt.title('Numerical Solution')
plt.xlabel('X')
plt.ylabel('Y')# 显示图像
plt.show()

---