1.5状态压缩DP

1.小国王

在 $n \times n$ 的棋盘上放 $k$ 个国王，国王可攻击相邻的 $8$ 个格子，求使它们无法互相攻击的方案总数。

输入格式
共一行，包含两个整数 $n$ 和 $k$ 。

输出格式
共一行，表示方案总数，若不能够放置则输出 $0$ 。

数据范围
$1 \leq n \leq 10,$
$0≤k≤n^{2}$
输入样例：

3 2

输出样例：

1.1题解

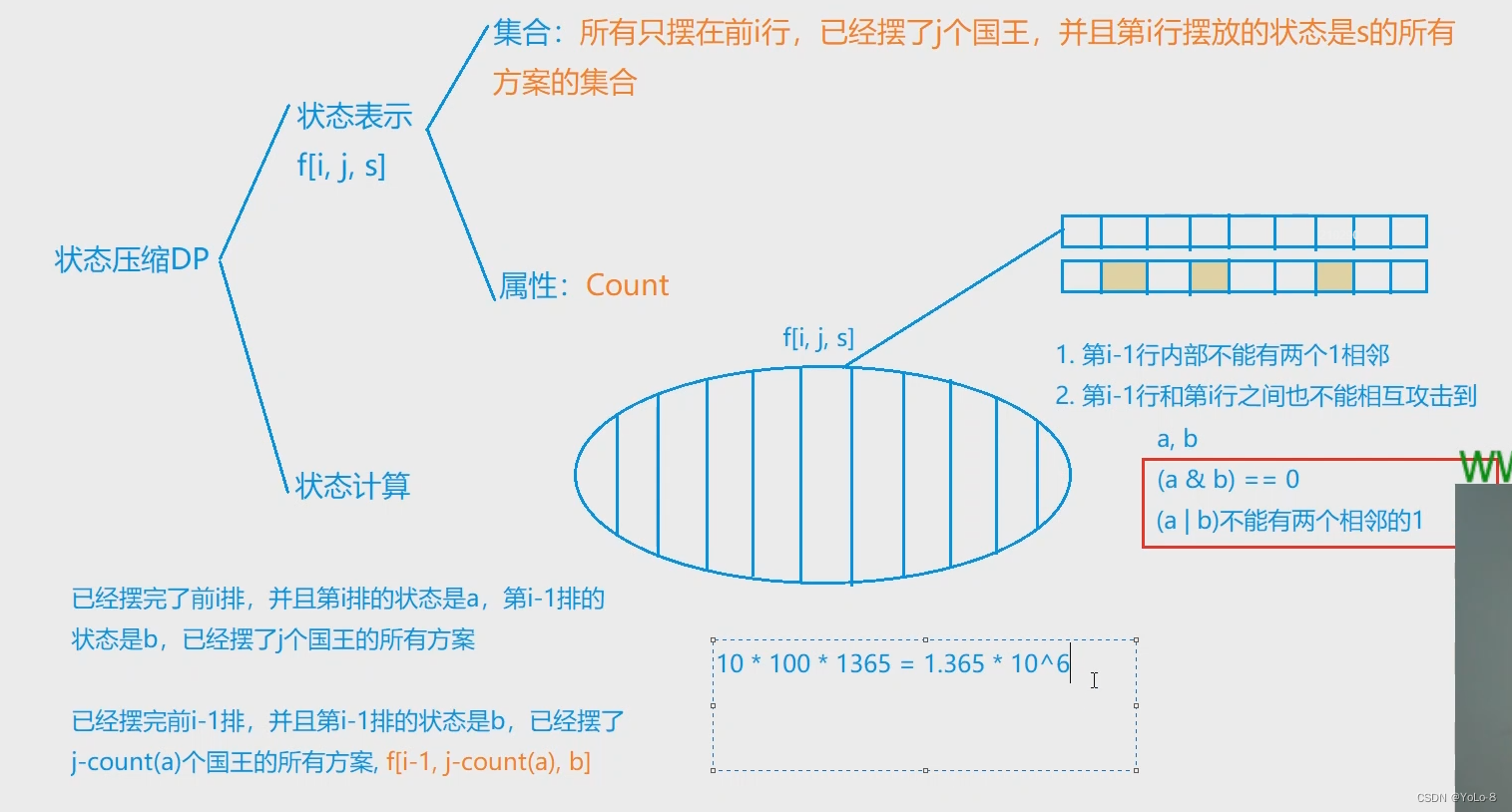
在这里插入图片描述

在这里插入图片描述
因此这会导致，两斜对角国王相互攻击。

综上所述，我们得到集合转移的约束条件。

下面是代码部分，有很详细的解说
在这里插入图片描述

1.2代码实现

#include<bits/stdc++.h>using namespace std;typedef long long LL;const int N = 12, M = 1 << 10, K = 110;int n,m;
int cnt[M]; //记录该状态中 1 的个数，即该状态所能摆放的国王个数
LL f[N][K][M]; //前 i 行已经摆好，且已摆放好 j 个国王，第 i 行状态是 a 的方案
vector<int> state; //合法的状态
vector<int> head[M]; //该状态能够转移的状态//判断该状态是否有相邻的 1，若没有则合法
bool check(int state)
{return !(state&state>>1);
}//统计该状态中 1 的个数
int count(int state)
{int res=0;for(int i=0;i<n;i++) res+=state>>i&1;return res;
}int main()
{cin>>n>>m;//筛选出合法的状态for(int i=0;i<1<<n;i++)if(check(i)){state.push_back(i);cnt[i]=count(i); //记录该状态中 1 的个数}//枚举出该状态所能转移到的状态for(int i=0;i<state.size();i++)for(int j=0;j<state.size();j++){int a=state[i],b=state[j];if(!(a&b)&&check(a|b)) //能够转移的条件head[a].push_back(b); //状态 a 和状态 b 之间可互相转移}f[0][0][0]=1;for(int i=1;i<=n+1;i++)for(int j=0;j<=m;j++)for(auto a : state) //枚举第 i 行的状态for(auto b : head[a]) //枚举第 i - 1 行的状态if(j>=cnt[a]) f[i][j][a]+=f[i-1][j-cnt[a]][b]; //状态 a 可由状态 b 转移过来// LL res=0;// for(auto x : state) res+=f[n][m][x];// cout<<res<<endl;// 上述代码等价于f[n+1][m][0]cout<<f[n+1][m][0]<<endl;return 0;
}

2.玉米田

农夫约翰的土地由 $M \times N$ 个小方格组成，现在他要在土地里种植玉米。

非常遗憾，部分土地是不育的，无法种植。

而且，相邻的土地不能同时种植玉米，也就是说种植玉米的所有方格之间都不会有公共边缘。

现在给定土地的大小，请你求出共有多少种种植方法。

土地上什么都不种也算一种方法。

输入格式

第 $1$ 行包含两个整数 $M$ 和 $N$ 。

第 $2.. M + 1$ 行：每行包含 $N$ 个整数 $0$ 或 $1$ ，用来描述整个土地的状况， $1$ 表示该块土地肥沃，0表示该块土地不育。

输出格式

输出总种植方法对 $10^{8}$ 取模后的值。

数据范围
$1 \leq M, N \leq 12$

输入样例：

2 3
1 1 1
0 1 0

输出样例：

2.1题解

在这里插入图片描述
算法构造
经典的棋盘型状态压缩动态规划，我们可以按照之前Acwing上P1064小国王的思路，处理本题。

首先，我们需要明确，题目的要求：

统计方案数
有些土地不能种植

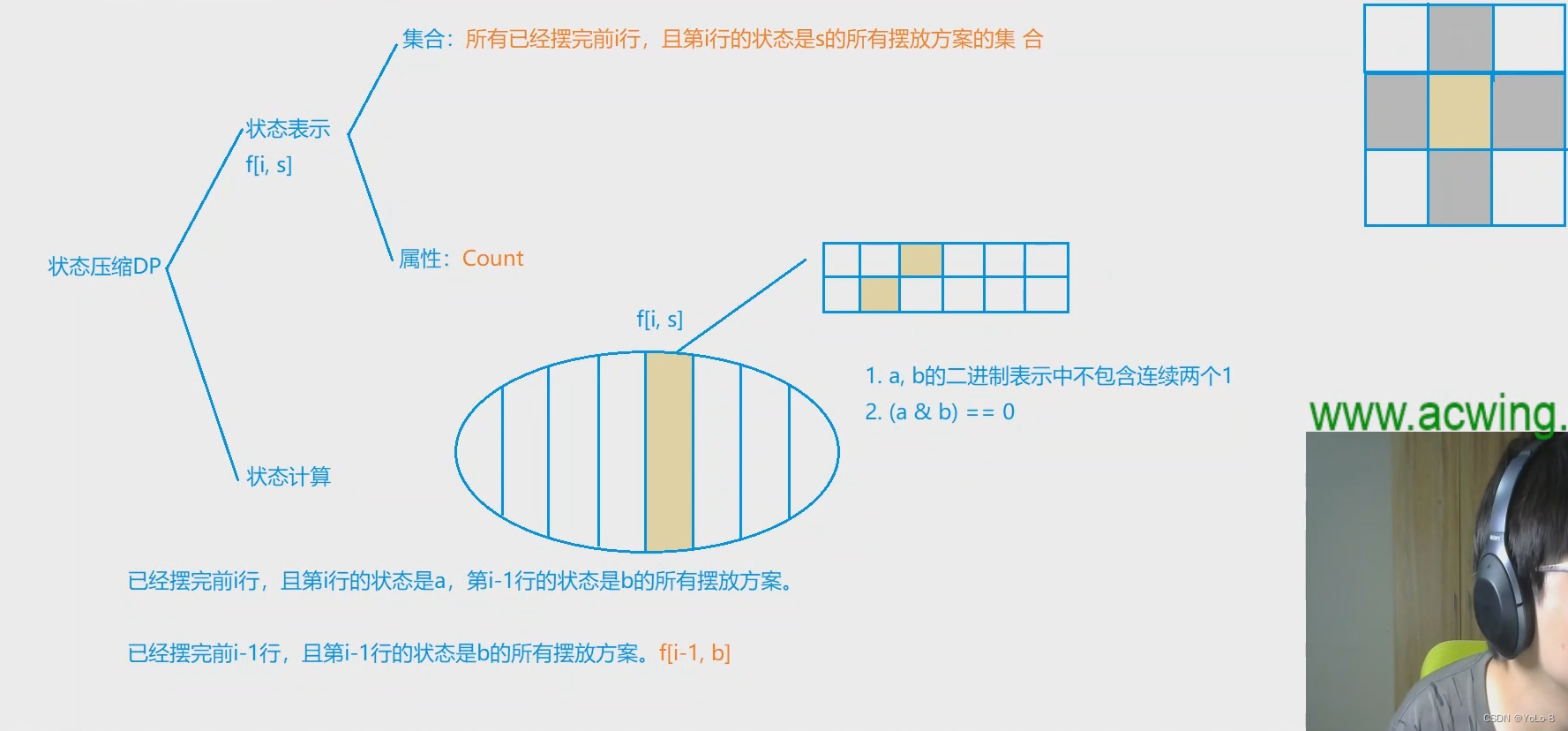
状态设计
首先，我们得明确状态是什么。

我们这个状态，肯定是要统计方案数。

我们这个状态，必然需要表示每一行土地种植的状态。

因此得到：

$f [i] [s] 表示已经种植前 i 行，且第 i 行种植的状态为 s 的方案数$

状态转移
题目的限制条件，其实就是我们转移的限制条件。

我们知道，这里是十字形的禁止种植，也就是上下左右不能有相邻的两棵玉米。

那么怎么判断呢？

如果说我们把 $1$ 表示这个地方种植玉米， $0$ 表示不种植
$S = 11101, 2, 3 这三个地方种玉米，第四个地方不种植玉米$

对于一行而言，不能种植相邻的玉米。

即：

对于一行而言，不能有相邻的 $1$
$S = 1110 是不合法的状态$

对于相邻的两行而言，不能在同一列都种植玉米

$a=1010\\ b=1000\\ 这是不可以的，在第一个位置会出现上下矛盾$
那么我们可以转化为：
在这里插入图片描述
最后，对于题目中的土地不能种植，我们可以认为。
$如果第 i 行的状态为 s ，那么荒废土地处不能有 1$

我们可以设计一个数组：
$g[i]表示第i行不能种植土地的状态\\g[1]=1011表示第一行，第一个，第三个，第四个位置不能种植玉米$
总而言之

在这里插入图片描述

2.2代码实现

#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>using namespace std;const int N = 14, M = 1 << 12, mod = 1e8;int n, m;
int w[N];
vector<int> state;
vector<int> head[M];
int f[N][M];//判断有没有相邻的两个1
bool check(int state)
{for (int i = 0; i + 1 < m; i ++ )if ((state >> i & 1) && (state >> i + 1 & 1))return false;return true;
}int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ )for (int j = 0; j < m; j ++ ){int t;cin >> t;//荒废土地是0，我们在次转换为1w[i] += !t * (1 << j);}for (int i = 0; i < 1 << m; i ++ )if (check(i))//这个状态不存在种植左右相邻的玉米state.push_back(i);for (int i = 0; i < state.size(); i ++ )for (int j = 0; j < state.size(); j ++ ){int a = state[i], b = state[j];if (!(a & b))//a对应的状态和j对应的状态没有在同一列种植玉米head[i].push_back(j);}f[0][0] = 1;for (int i = 1; i <= n + 1; i ++ )for (int j = 0; j < state.size(); j ++ )//在第i行，状态j是否满足在荒废土地上种植玉米if (!(state[j] & w[i]))//从上一行j对应的状态，转到本行i对应的状态for (int k : head[j])f[i][j] = (f[i][j] + f[i - 1][k]) % mod;//表示第n+1行什么都没种植的状态，其实就是累加f[n][S]cout << f[n + 1][0] << endl;return 0;
}