本节将概括目前为止所学的张量积知识。并讨论一般张量,它可以由任意数量的向量和协向量的任意组合来生成。
同样,也是使用的非标准的符号。
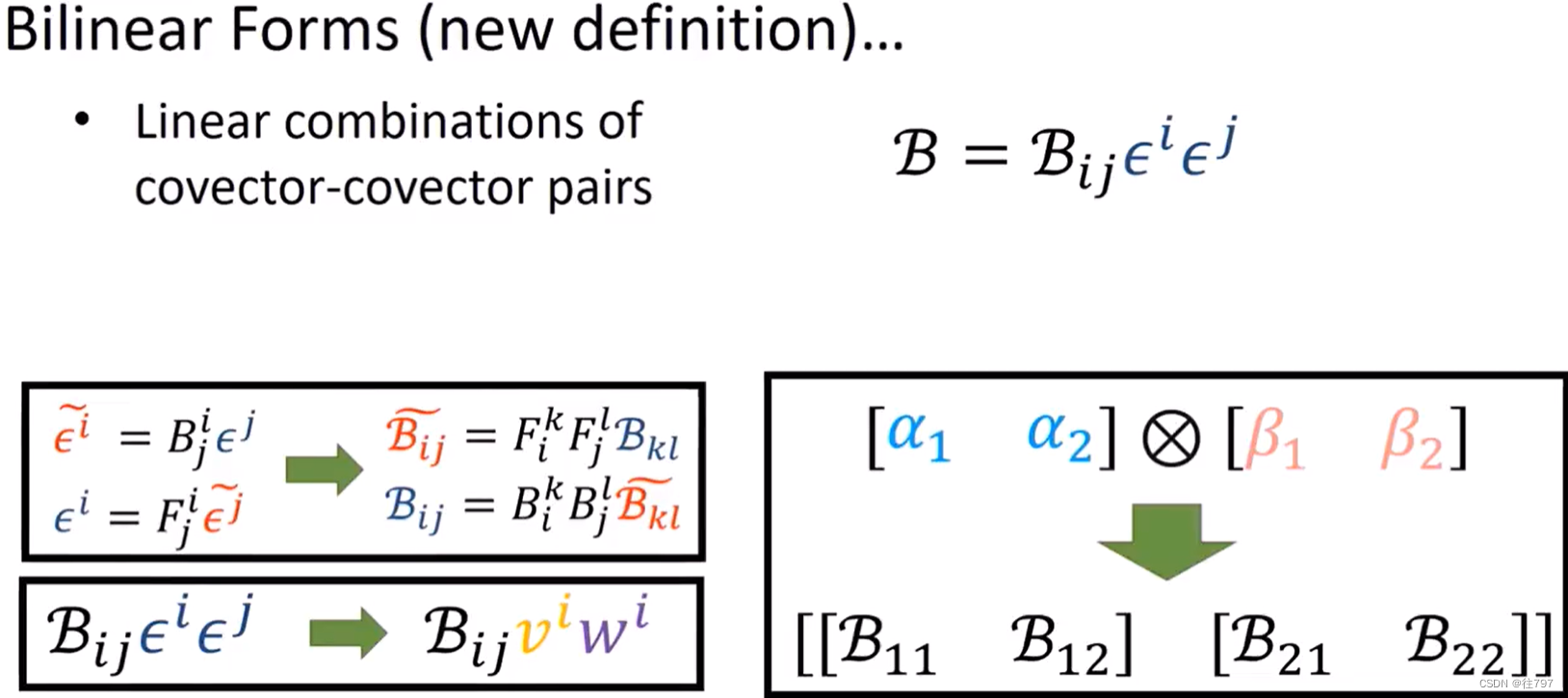
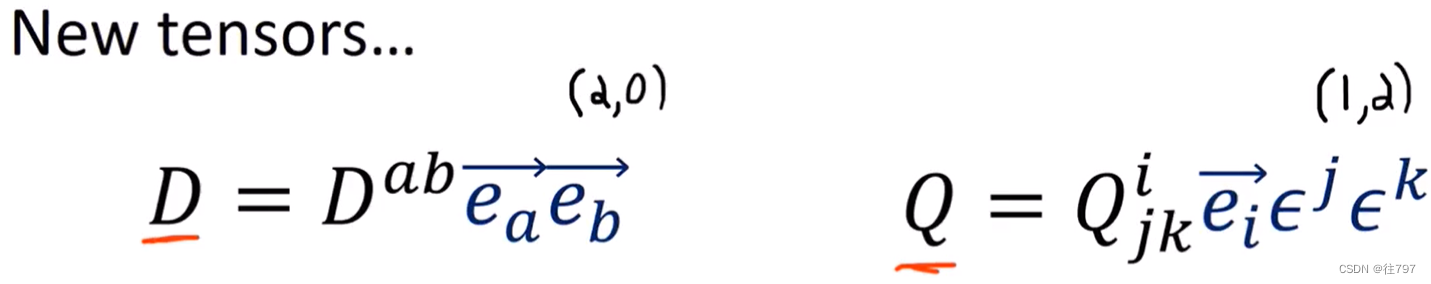
(2,0)阶张量, 由两个向量生成的。 (1,2)阶张量,由1个向量和2个协向量生产。
由此产生三个问题,
1.坐标变换规则是什么?
2、Q作用于输入D的作用的乘法公式是什么?
3、数组的形状是什么》?

第一个问题

第二个问题
这个问题有些棘手,因为事实证明没有单一的方法可以让Q作用于D。 这是什么意思呢?
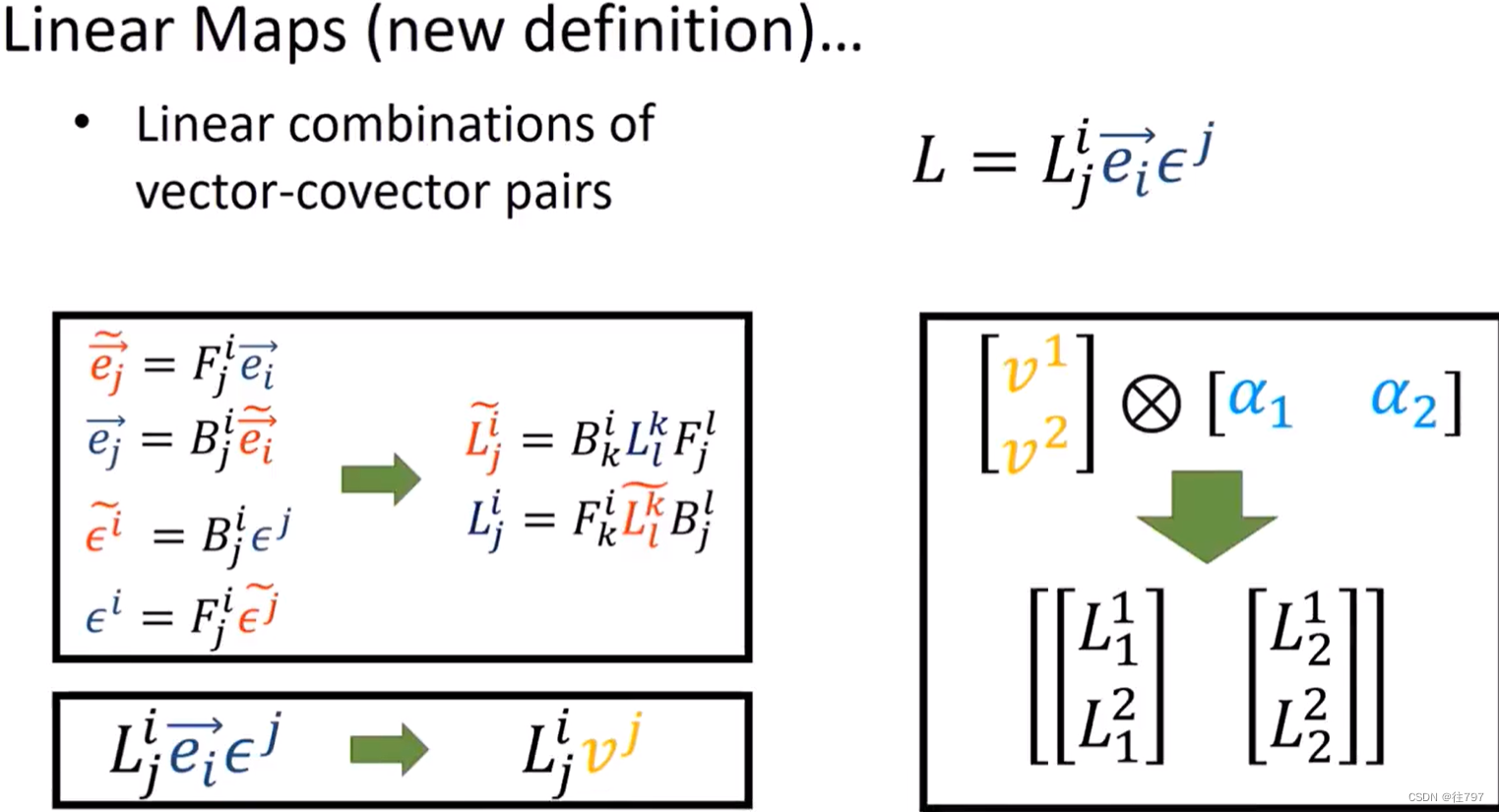
以线性映射L作用于向量V为例,
将L , V展开成线性组合的形式,
可看到,L只有一个协向量,V只有一个向量,
所以,只有可能发生的一件事是:必须作用于
。

所以是,只有一种可能的答案。
但是,Q与D是更大的张量,展开线性组合后会具有更多的向量和协向量,
对于问题Q(D)的答案是什么,有很多种可能的答案。
原因是我们可通过多种可能的方式将这些输入向量传递给这些协向量。

需要说明的一点是, 随着张量越来越大,协变和逆变部分越来越多,我们最终会得到越来越多的求和方法以及越来越多的方法计算函数。
所以,你直接写个Q(D)在这问结果是啥,有点模棱两可,并没有确切地告诉我们该怎么做。
要说出我们的真正意思,我们通常需要用爱因斯坦符号写出来,
像这样:

,
第三个问题:

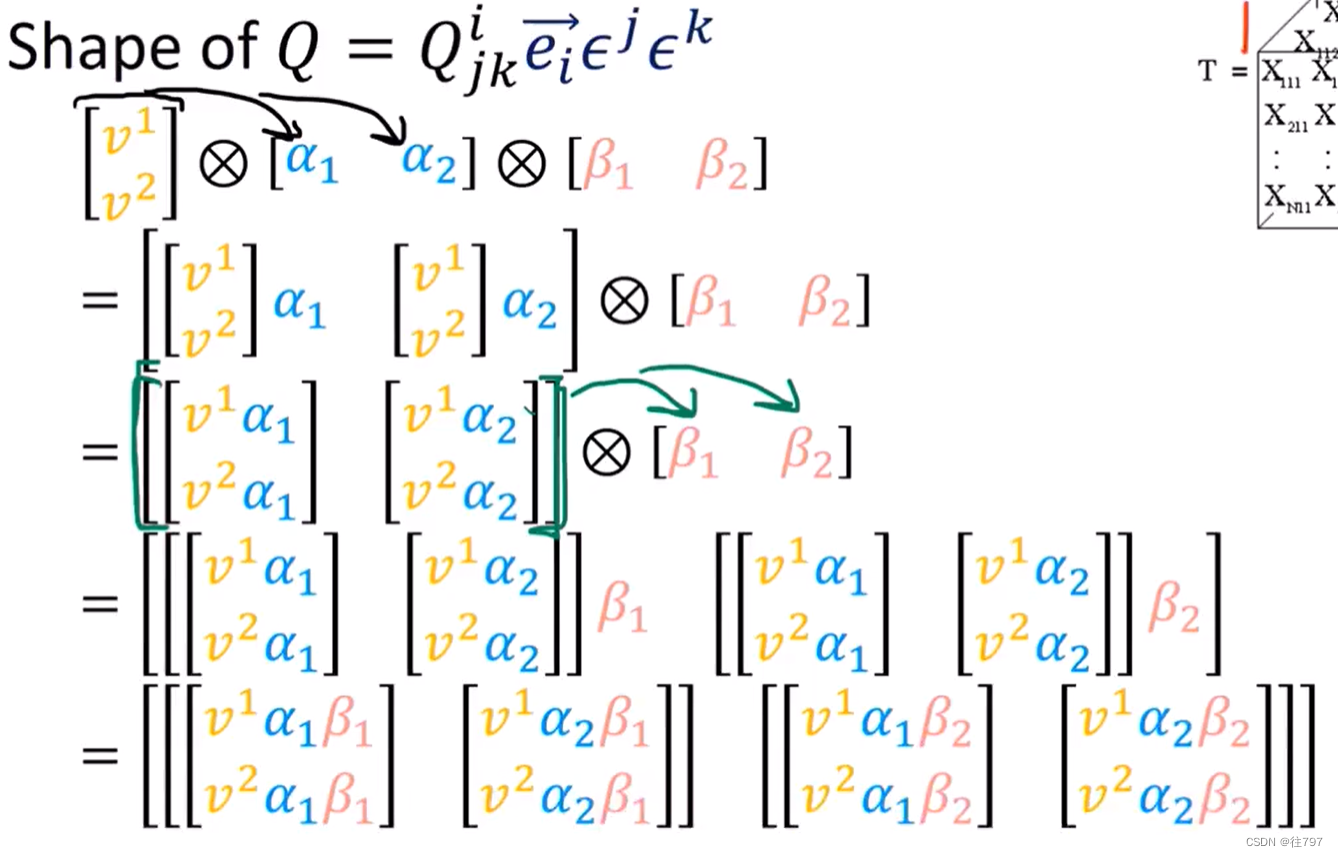
将张量写成数组 有用的部分原因是因为它 为我们提供一种使用标准行列乘法规则执行分量乘法的完全机械方式。
例如,想得到这么个矩阵:

它是一行列(a row of column),要作用于这个列向量,我只需使用标准的行列乘法规则,
即第一次加第二次(first-times-first plus second-times-second) , 并且我得到了正确的列向量作为结果。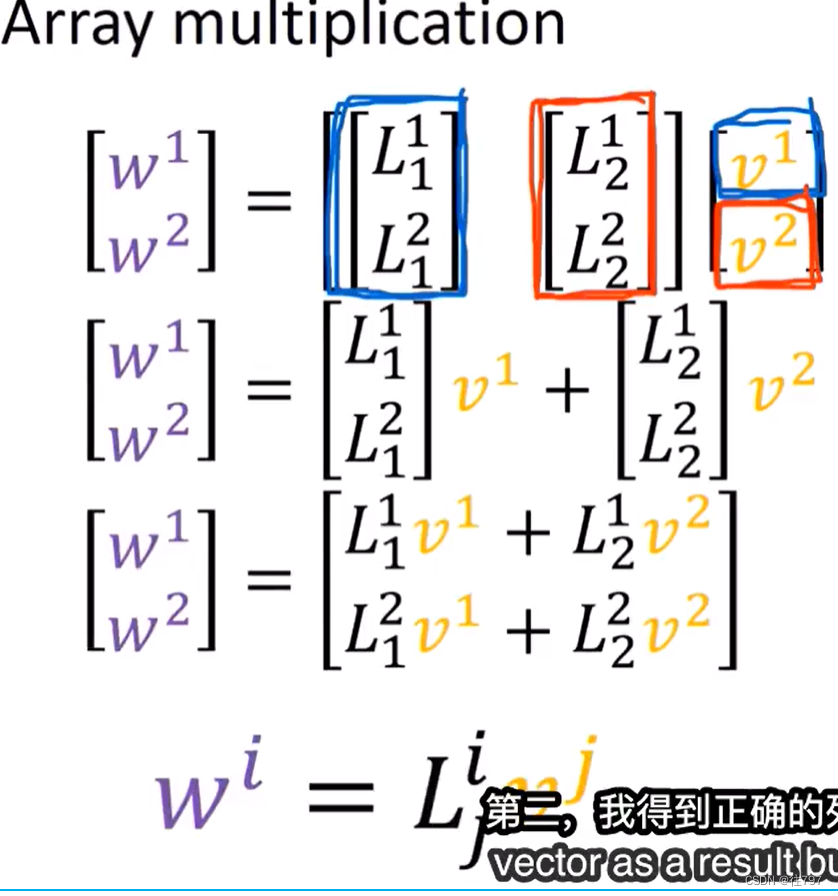
但不幸的是,对于较大的张量,如前面的Q和D,具有高阶数(high type numbers),有几种可能的乘法规则,正如我们之前讨论的那样,因此,没有简单的方法来进行数组乘法来保证给我们 我们想要的答案,。。

所以,对于高阶张量(high type tensors) , 数组表示变得不太有用,并且倾向于使用更紧凑的爱因斯坦符号来描述组件的乘法规则。
所以,对于高阶张量(high type tensors),抽象符号和数组符号有其局限性。
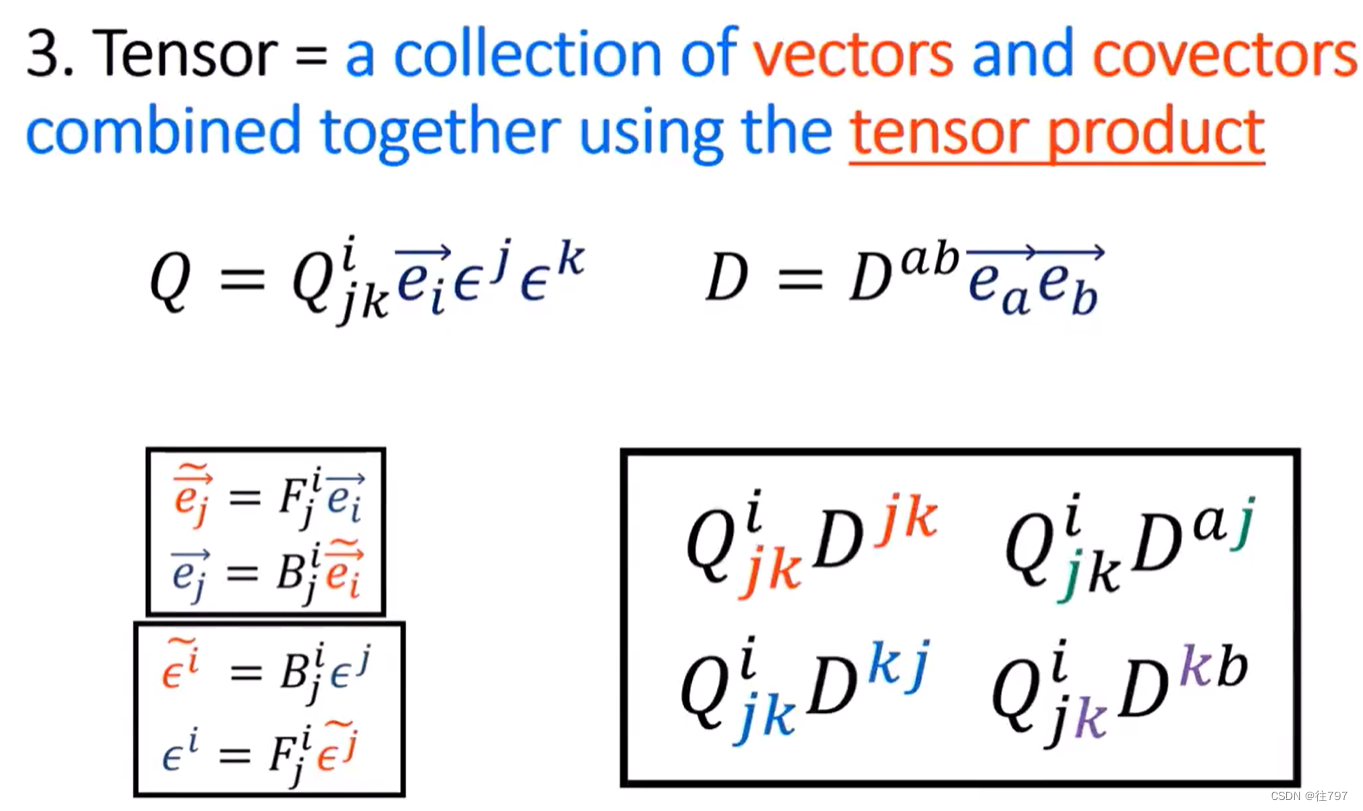
还是没有感受到这为啥是最好的定义。
处理高阶张量的张量乘法时,可将张量抽象地写出来,或者写成数组,通常最好用爱因斯坦分量符号写出来,因为它使得求和规则非常明显。