Floyd
Floyd 算法,是一种在图中求任意两点间最短路径的算法。
Floyd 算法适用于求解无负边权回路的图。
时间复杂度为 O ( n 3 ) O(n^3) O(n3),空间复杂度 O ( n 2 ) O(n^2) O(n2)。
对于两点 ( i , j ) (i,j) (i,j) 之间的最短路径,有两种可能:从 i i i 直接到 j j j,或者从 i i i 经过若干结点 k k k 到 j j j。
设 f ( k , i , j ) f(k,i,j) f(k,i,j) 为以 k k k 为中转结点时 i i i, j j j 两点间最短路径。
递推转移方程: f ( i , j , k ) = min ( f ( k − 1 , i , j ) , f ( k − 1 , i , k ) + f ( k − 1 , k , j ) ) f(i,j,k)=\min(f(k-1,i,j),f(k-1,i,k)+f(k-1,k,j)) f(i,j,k)=min(f(k−1,i,j),f(k−1,i,k)+f(k−1,k,j))。
滚动数组可以优化为二维数组,即 f ( i , j ) f(i,j) f(i,j)。
核心代码:
for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
预处理操作:
- 将递推数组
memset为无穷大 - 令 f ( i , i ) = 0 f(i,i)=0 f(i,i)=0,即自己和自己距离为 0 0 0
- 读入 ( u , v ) (u,v) (u,v) 之间边权的同时更新 f ( u , v ) f(u,v) f(u,v),无向图无需双向赋值
Dijkstra
单源最短路径问题(SSSP),我们通常使用 Dijkstra 算法。Dijkstra 算法,本质上是使用 BFS 和贪心解决单源图最短路径的问题。虽然但是,Dijkstra 算法不适用于有负边权的图。
所谓单源图,顾名思义,就是规定只有一个起点的图。
对于求解的图,假设任意两顶点之间距离为正无穷。然后开始加入边,更新当前源点与其他顶点的最短距离。将除起点外所有点加入未知集合,并将起点加入已知集合,直至确定该点到起点最短路径;依次更新起点到 i i i 的距离
dis[i],将未知集合dis中与起点距离最小的 x x x 加入已知集合;用 Floyd 的思想,若起点与 n n n 间距离大于起点到 x x x 距离加 x x x 到 n n n 距离,更新dis[n],更新与它相连的点;重复以上步骤直到终点进入已知集合即可。
我们可以用优先队列造小顶堆解决问题。
我们先把每一条边按照举例排序构造小顶堆,然后依次进行操作。
举个栗子,以下图为例:
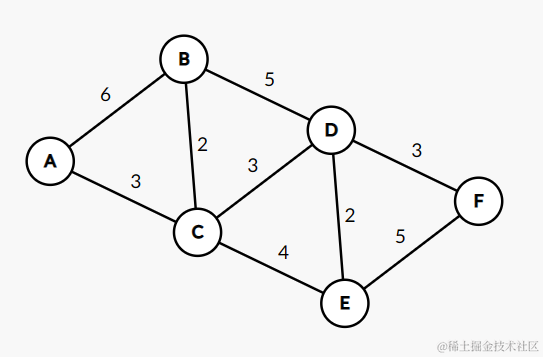
Dijkstra 的基本思想,其实是先把每一个点的 dis 修改为无穷大,然后开始找最小 dis 点,然后枚举以该点为中转点到达的点比较路径长度试图修改。以 A A A 为源点,枚举当前点可以到达的点,第一次我们可以修改 B B B、 C C C 的dis;此时 dis 最小的点为 C C C,所以下一次我们以 C C C 为中转点尝试转移,显然可以改变 dis[D]、dis[E],由于以 C C C 为中转点到 B B B 的距离更优,所以 B B B 也可以被修改,以此类推。
时间复杂度为 O ( m log n ) O(m\log n) O(mlogn), n n n 为顶点数, m m m 为边数。
struct node
{int u,dis;friend bool operator < (node a,node b){return a.dis>b.dis;//小顶堆!}
};priority_queue<node> q;void dij(int s)//s表示源点
{memset(diss,0x7f,sizeof(diss));diss[s]=0;q.push(node{s,0});while(!q.empty()){int u=q.top().id;q.pop();if(vis[u]) continue;vis[u]=1;for(int i=head[u];i;i=nxt[i]){if(diss[to[i]]>diss[u]+w[i]){diss[to[i]]=diss[u]+w[i];q.push(node{to[i],diss[to[i]]});}}}
}
练手板子题
代码如下:
#include <bits/stdc++.h>
using namespace std;const int maxn=2*1e5+5;
int head[maxn],nxt[maxn],to[maxn],w[maxn],cnt,dis[maxn],vis[maxn];void add(int x,int y,int z)
{to[++cnt]=y;w[cnt]=z;nxt[cnt]=head[x];head[x]=cnt;
}struct node
{int id,dis;friend bool operator < (node a,node b){return a.dis>b.dis;//小顶堆!}
};priority_queue<node> q;void dij(int s)
{memset(vis,0,sizeof(vis));memset(dis,0x3f,sizeof(dis));dis[s]=0;q.push(node{s,0});while(!q.empty()){int u=q.top().id;q.pop();if(vis[u]) continue;vis[u]=1;for(int i=head[u];i;i=nxt[i])if(dis[to[i]]>dis[u]+w[i])dis[to[i]]=dis[u]+w[i],q.push(node{to[i],dis[to[i]]});}
}int main()
{int n,m,s,u,v,w;cin>>n>>m>>s;for(int i=1;i<=m;i++) cin>>u>>v>>w,add(u,v,w);dij(s);for(int i=1;i<=n;i++) cout<<dis[i]<<' ';return 0;
}
SPFA
SPFA 其实是 Bellman-Ford 算法的队列优化算法的别称,常用于求含负边权的单源最短路径(参见 Johnson 算法)以及判负权环。
关于什么是负环,一条边权和为负数的回路就是负环。如果一个点被加入队列的次数大于等于总点数,那么不存在最短路,即一定存在负环。
最坏情况下,SPFA 算法的时间复杂度为 O ( V E ) O(VE) O(VE)(边数 × \times ×点数)。
SPFA 的流程为,每次从队列中取出队首点,尝试更新与这个点相连的点的 dis,若可以更新就将其入队。
代码如下:
void spfa()
{memset(dis,0x3f3f3f,sizeof(vis));dis[s]=0;z[top=1]=s;for(int j=1;j<=top;j++){int now=z[j];vis[now]=0;for(int head[now];i;i=nxt[i])if(dis[to[i]]>dis[now]+w[i]){dis[to[i]]=dis[now]+w[i];if(!vis[to[i]]) vis[to[i]]=1,z[++top]=to[i];}}
}
练手板子题
代码如下:
#include <bits/stdc++.h>
using namespace std;const int maxn=40005;
int nxt[maxn],to[maxn],head[maxn],val[maxn],dis[maxn],vis[maxn],rec[maxn],cnt,n,m;
queue<int> q;void add(int x,int y,int z)
{to[++cnt]=y;val[cnt]=z;nxt[cnt]=head[x];head[x]=cnt;
}bool spfa()
{memset(dis,127,sizeof(dis));memset(vis,0,sizeof(vis));memset(rec,0,sizeof(rec));while(!q.empty) q.pop();q.push(1);dis[1]=0,vis[1]=1,rec[1]++;while(!q.empty()){int u=q.front();q.pop();vis[u]=0;//队首已出队for(int i=head[u];i;i=nxt[i]){if(dis[to[i]]>dis[u]+val[i]){dis[to[i]]=dis[u]+val[i];//对于判断是否有负环,用数组rec记录点的入队次数,如果入队次数>n,就证明出现了负环导致没有最短路if(!vis[to[i]]) vis[to[i]]=true,rec[to[i]]++,q.push(to[i]);//能更新,压入队列if(rec[to[i]]>=n) return true;}} }return false;
}int main()
{int T,u,v,w;cin>>T;while(T--){cin>>n>>m;memset(head,0,sizeof(head));cnt=0;for(int i=1;i<=m;i++){cin>>u>>v>>w;add(u,v,w);if(w>=0) add(v,u,w);}if(spfa()) cout<<"YES"<<endl;else cout<<"NO"<<endl;}return 0;
}
Johnson
Johnson 全源最短路算法,顾名思义就是一个名为 Johnson 的大神发明的一种求全源最短路的算法。可以解决图中任意起点的最短路问题。
首先考虑一种逆天的朴素做法,每次取一个点去跑 SPFA,时间复杂度 O ( m n 2 ) O(mn^2) O(mn2)(点数 × \times × 边数);或者干脆直接跑 O ( n 3 ) O(n^3) O(n3) 的 Floyd。显然这都是会炸掉的。
所以我们考虑一种很强的单源最短路径算法——Dijkstra。但是 Dijkstra 不能解决负边权,怎么办?
第一反应是把所有边的边权都加上一个数使其非负,但是显然可以被 Hack 掉:
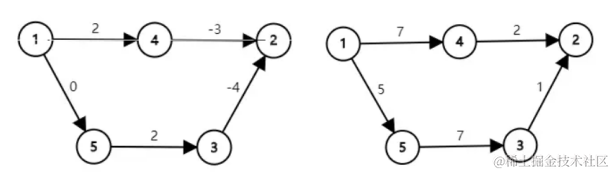
对于上图,我们惊奇地发现,原先 1 1 1 到 2 2 2 的最短路是 1 → 5 → 3 → 2 1\rightarrow5\rightarrow3\rightarrow2 1→5→3→2,结果变成正的之后最短路变成 1 → 4 → 2 1\rightarrow4\rightarrow2 1→4→2 了,寄。
Johnson 算法登场!它是一种可以替代上面逆天的负边权转正方法的算法。
我们新建一个虚拟节点编号为 0 0 0,这个点向其他所有点都连一条边权为 0 0 0 的边。然后跑一遍 SPFA,统计 0 0 0 到所有其他结点的最短路长度 h i h_i hi(为什么叫 h h h 是因为《算法导论》里这么叫)。如果存在一条边 u → v u\rightarrow v u→v 边权为 w w w,那么将该边边权重新设置为 w + h u − h v w+h_u-h_v w+hu−hv。
重新设置边权之后,我们就可以对于每一个节点跑一遍 Dijkstra 了。总时间复杂度 O ( n m log m ) O(nm\log m) O(nmlogm)。
如何证明 Johnson 算法的正确性?
首先我们证明经过这样一波操作之后最短路不会变。对于原最短路 s → p 1 → p 2 → ⋯ → p k → t s\rightarrow p_1\rightarrow p_2\rightarrow\cdots\rightarrow p_k\rightarrow t s→p1→p2→⋯→pk→t,用 Johnson 算法改变边权之后的长度可以表示为 ( w ( s , p 1 ) + h s − h p 1 ) + ( w ( p 1 , p 2 ) + h p 1 − h p 2 ) + ⋯ + ( w ( p k , t ) + h p k − h t ) (w(s,p_1)+h_s-h_{p_1})+(w(p_1,p_2)+h_{p_1}-h_{p_2})+\cdots+(w(p_k,t)+h_{p_k}-h_t) (w(s,p1)+hs−hp1)+(w(p1,p2)+hp1−hp2)+⋯+(w(pk,t)+hpk−ht),化简之后为 w ( s , p 1 ) + w ( p 1 , p 2 ) + ⋯ + w ( p k , t ) + h s − h t w(s,p_1)+w(p_1,p_2)+\cdots+w(p_k,t)+h_s-h_t w(s,p1)+w(p1,p2)+⋯+w(pk,t)+hs−ht。如果原先的 s → t s\rightarrow t s→t 为最短路,那么更改之后其实就是加了个 h s − h t h_s-h_t hs−ht,因为这个 h s − h t h_s-h_t hs−ht 是定值,所以说原先的最短路和改变边权之后的最短路显然是一条路径因为原先要经过的点必须经过而无论中间取什么点都不可能改变加上的 h s − h t h_s-h_t hs−ht 的值,所以在新图上我们跑 Dijkstra 得到的最短路经过的点一定和原图相同。
接下来证明为什么边权处理之后一定非负。对于图中任意一条边 ( u , v ) (u,v) (u,v),一定满足 h v ≤ h u + w ( u , v ) h_v\leq h_u+w(u,v) hv≤hu+w(u,v),这是显然的,因为从 0 0 0 到 v v v 的最短路不可能超过从 0 0 0 到 u u u 的最短路加上 ( u , v ) (u,v) (u,v) 的边权,否则就会被松弛更新,其实这就是图论中的三角形不等式,最短路上的所有边都满足三角形不等式。于是乎用 Johnson 算法更改后的边权 w ′ ( u , v ) = w ( u , v ) + h u − h v w'(u,v)=w(u,v)+h_u-h_v w′(u,v)=w(u,v)+hu−hv 一定是非负的,完结撒花!
练手板子题
代码如下:
#include <bits/stdc++.h>
using namespace std;
#define int long longconst int maxn=9005,maxx=1e9;//注意原有m条边+新建0节点n条边,数组小了会炸
int nxt[maxn],head[maxn],cnt,to[maxn],w[maxn],h[maxn],vis[3005],tim[3005],m,n,u,v,ww,dis[3005];void add(int x,int y,int z)
{to[++cnt]=y;w[cnt]=z;nxt[cnt]=head[x];head[x]=cnt;
}bool spfa()//SPFA判负环
{queue<int> q;memset(h,127/3,sizeof(h));h[0]=0,vis[0]=1;q.push(0);while(!q.empty()){int u=q.front();q.pop();vis[u]=0;for(int i=head[u];i;i=nxt[i]){int v=to[i];if(h[v]>h[u]+w[i]) {h[v]=h[u]+w[i];if(!vis[v]) {q.push(v),vis[v]=1,tim[v]++;if(tim[v]>n) return true;}}}}return false;
}struct node
{int id,dis;bool friend operator < (node a,node b){return a.dis>b.dis;}
};void dij(int s)
{priority_queue<node> q;memset(vis,0,sizeof(vis));for(int i=1;i<=n;i++) dis[i]=maxx;dis[s]=0;q.push(node{s,0});while(!q.empty()){int u=q.top().id;q.pop();if(vis[u]) continue;vis[u]=1;for(int i=head[u];i;i=nxt[i])if(dis[to[i]]>dis[u]+w[i])dis[to[i]]=dis[u]+w[i],q.push(node{to[i],dis[to[i]]});}
}signed main()
{cin>>n>>m;for(int i=1;i<=m;i++) cin>>u>>v>>ww,add(u,v,ww);for(int i=1;i<=n;i++) add(0,i,0);if(spfa()) cout<<-1,exit(0);for(int u=1;u<=n;u++) for(int i=head[u];i;i=nxt[i]) w[i]+=h[u]-h[to[i]];for(int i=1;i<=n;i++){dij(i);int ans=0;for(int j=1;j<=n;j++){if(dis[j]==maxx) ans+=j*maxx;else ans+=j*(dis[j]+h[j]-h[i]);}cout<<ans<<endl;}return 0;
}
总结
(下表中 m m m 为边数, n n n 为点数)
| 最短路算法 | Floyd | SPFA | Dijkstra | Johnson |
|---|---|---|---|---|
| 最短路类型 | 每对结点之间的最短路 | 单源最短路 | 单源最短路 | 每对结点之间的最短路 |
| 适配的图 | 任意图 | 任意图 | 非负权图 | 任意图 |
| 能否检测负环 | 能 | 能 | 不能 | 能 |
| 时间复杂度 | O ( n 3 ) O(n^3) O(n3) | O ( n m ) O(nm) O(nm) | O ( m log m ) O(m\log m) O(mlogm) | O ( n m log m ) O(nm\log m) O(nmlogm) |