一言

已知n个顶点，选n-1条最短的边，不可成环。

概述

克鲁斯卡尔（Kruskal）算法是用来求加权连通图的最小生成树的算法。其基本思想是按照权值从小到大的顺序选择n-1条边，保证这n-1条边不构成回路。
这就要求要首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止。
也就是说：

1. 要对边的权值进行排序；
2. 不停加入新边且不能产生回路；

举个“栗”子

不妨从下面这个场景说起

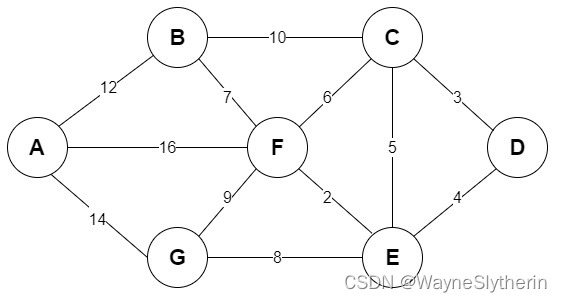
郝乡长在光荣完成了德胜乡七个村子的修路任务之后，心情非常的好。因为他觉得之前悬而未决的交通巡检问题似乎也可以借鉴此前的宝贵经验。原来，得胜乡又七个集市（A-G），每逢过节都是人山人海，为了群众的安全，连贯的巡检是很必要的，可是如何设计连通七个集市的巡检路线呢？要短！要连贯！要高效！

图解

首先，不同的连接方式其权值总和也不同，如何找到最优解是关键。

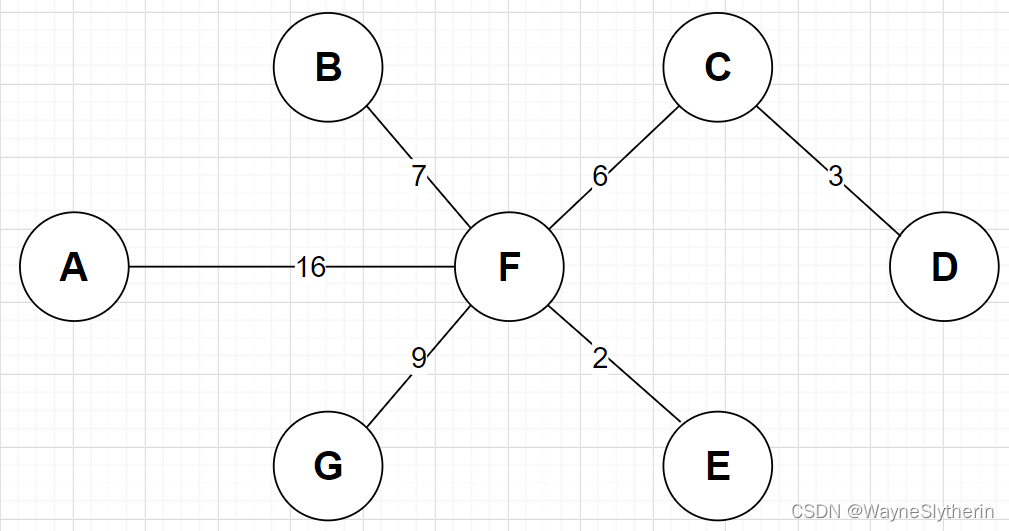
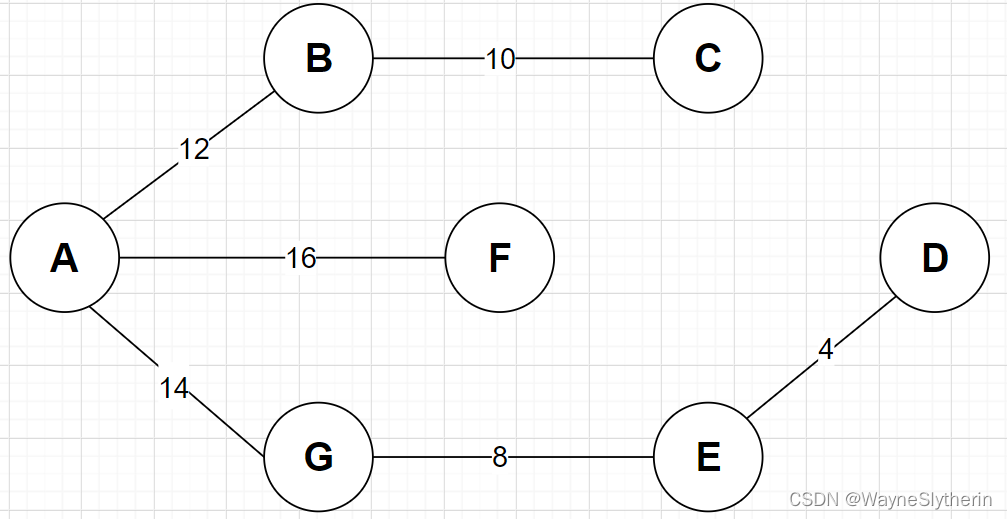
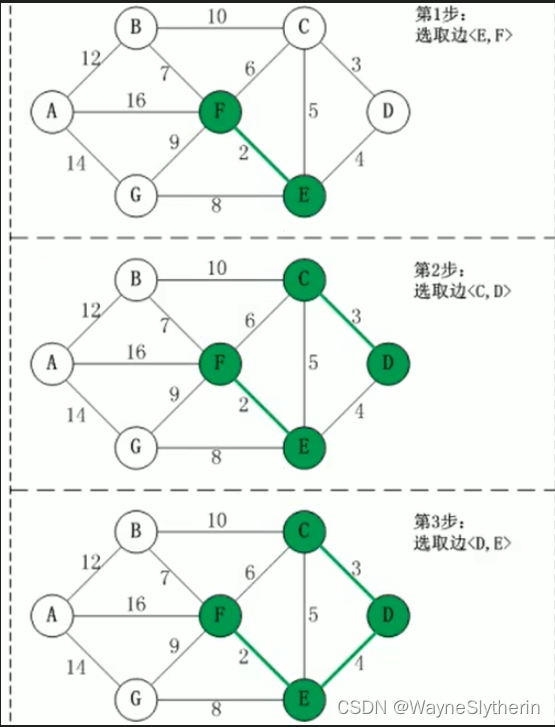
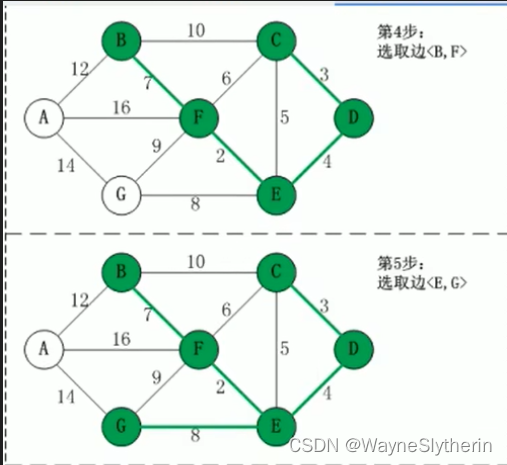
最后合龙，得到最优解

第1步: 将边<E,F>加入R 中边<E,F>的权值最小，因此将它加入到最小生成树结果 R 中
第2步: 将边<C,D>加入 R 中。上一步操作之后，边<C,D>的权值最小，因此将它加入到最小生成树结果 R 中
第3步: 将边<D,E>加入 R 中。上一步操作之后，边<D,E>的权值最小，因此将它加入到最小生成树结果 R 中
第4步: 将边<B,F>加入R 中。上一步操作之后，边<C,E>的权值最小，但<C,E>会和已有的边构成回路因此，跳过边<C,E>。同理，跳过边<C,F>。将边<B,F>加入到最小生成树结果R中。
第5步: 将边<E,G>加入 R 中。上一步操作之后，边<E,G>的权填最小，因此将它加入到最小生成树结果 R中
第6步: 将边<A,B>加入R 中。上一步操作之后，边<F,G>的权值最小，但<F,G>会和已有的边构成回路:因此，跳过边<F,G>。同理，跳过边<B,C>。将边<A,B>加入到最小生成树结果R中。

分析

根据前面介绍的克鲁斯卡尔算法的基本思想和做法，我们能够了解到，克鲁斯卡尔算法重点需要解决的以下两个问题:

1. 对图的所有边按照权值大小进行排序。
2. 将边添加到最小生成树中时，怎么样判断是否形成了回路。
   对于1 ，很好解决，采用排序算法进行排序即可。
   对于2，可以记录顶点在"最小生成树"中的终点，顶点的终点是"在最小生成树中与它连通的最大顶点”。然后每次需要将一条边添加到最小生存树时判断该边的两个顶点的终点是否重合，重合的话则会构成回路。

如何判断回路

我们假定C->D->E->F连通，则此四个顶点实际都有终点：
C->F
D->F
E->F
F->F
终点的概念实际上就是避免二次访问，最小生成树要求每个点到另一个点都只有一种可能。以上例再加入CE边为例，在CE加入之前，从C到E已经有了CD->DE的方案，那么就不允许再引入CE这个方案。采用终点验证的方法实际上是把这个思路进行了归纳扩展。

代码实现

public class KruskalCase {private int edgeNum;//边的个数private char[]vertexs;//顶点数组private int[][]matrix;//邻接矩阵private static final int INF = Integer.MAX_VALUE;//使用INF表示两个顶点不能连同public static void main(String[] args) {//测试char[] vertexs = {'A','B','C','D','E','F','G'};int matrix[][] = {/*A* *B*  *C*  *D* *E* F  *G* *//*A*/  {0  ,12 ,INF,INF,INF,16 ,14 },/*B*/  {12 ,0  ,10 ,INF,INF,7  ,INF},/*C*/  {INF,10 ,0  ,3  ,5  ,6  ,INF},/*D*/  {INF,INF,3  ,0  ,4  ,INF,INF},/*E*/  {INF,INF,5  ,4  ,0  ,2  ,8  },/*F*/  {16 ,7  ,6  ,INF,2  ,0  ,9  },/*G*/  {14 ,INF,INF,INF,8  ,9  ,0  }};//创建KruskalCase 对象实例KruskalCase kruskalCase = new KruskalCase(vertexs, matrix);//输出构建的kruskalCase.print();//        EData[] edges = kruskalCase.getEdges();
//        System.out.println("排序前："+Arrays.toString(edges));//未排序
//        kruskalCase.sortEdges(edges);//排序
//        System.out.println("排序后："+Arrays.toString(edges));//排序后kruskalCase.kruskal();}//构造器public KruskalCase(char[] vertexs, int[][] matrix) {//初始化顶点数和边个数int vlen = vertexs.length;//初始化顶点this.vertexs = vertexs;//初始化边this.matrix = matrix;//统计边的条数for (int i = 0; i < vlen; i++) {for (int j = i+1; j < vlen; j++) {if (this.matrix[i][j]!=INF){edgeNum++;}}}}//克鲁斯卡尔算法核心public void kruskal(){int index =0;//表示最后结果数组的索引int [] ends = new int[edgeNum];//用于保存“已有最小生成树”中的每个顶点在最小生成树中的终点//创建结果数组，保存最后的最小生成树EData [] rets = new EData[edgeNum];//获取图中所有的边的集合，一共有12条边EData[] edges = getEdges();System.out.println("图的边的集合："+Arrays.toString(edges)+"。共"+edges.length+"条边。");//12//按照边的权值大小进行排序（从小到大）sortEdges(edges);//遍历edges数组，将边添加到最小生成树，判断准备加入的边是否构成回路，如果没有就加入rets,否则不能加入for (int i = 0; i < edgeNum; i++) {//获取第i条边的第1个顶点int p1 = getPosition(edges[i].start); // 比如边<E,F>, p1为4//获取第i条边的第2个顶点int p2 = getPosition(edges[i].end);   // 比如边<E,F>, p2为5//获取p1这个顶点在已有的最小生成树中的终点int m = getEnd(ends,p1);              //在上面的比如中，m=4//获取p2这个顶点在已有的最小生成树中的终点int n = getEnd(ends,p2);            //在上面的比如中，n=5//是否构成回路if (m!=n){//不构成回路//设置m在已有“最小生成树”中的终点。比如第一次：<E,F> [0,0,0,0,0,0,0,0,0,0,0,0] => [0,0,0,0,5,0,0,0,0,0,0,0]//对end数组的理解：第4位值为5，表示第4个顶点（E）的终点是第5个顶点（F）ends[m] = n;rets[index++] = edges[i];//边入选}}//统计并打印“最小生成树”，输出retsfor (int i = 0; i < index; i++) {System.out.println("最小生成树为=" + rets[i]);}}//打印邻接矩阵public void print(){System.out.println("邻接矩阵为：\n");for (int i = 0; i < vertexs.length; i++) {for (int j = 0; j < vertexs.length; j++) {System.out.printf("%12d\t",matrix[i][j]);}System.out.println();}}//边的排序（按权值），冒泡排序/*** @param edges 边的集合*/private void sortEdges(EData[]edges){for (int i = 0; i < edges.length-1; i++) {for (int j = 0; j < edges.length-1-i; j++) {if (edges[j].weight>edges[j+1].weight){//交换EData tmp =edges[j];edges[j] = edges[j+1];edges[j+1] = tmp;}}} }/*** @param ch 顶点的值， ‘A’，‘B’等* @return 返回ch顶点对应的下标，如果找不到返回-1*/private int getPosition(char ch){for (int i = 0; i < vertexs.length; i++) {if (vertexs[i]==ch)return i;}return -1;}/*** 获取图中的边，放到EData[]数组中，后面我们需要遍历该数组，通过matrix邻接矩阵来获取* EData[]形式 [['A','B',12],['B','F',7],......]* @return*/private EData[] getEdges(){int index = 0 ;EData[] edges = new EData[edgeNum];for (int i = 0; i < vertexs.length; i++) {for (int j = i+1; j < vertexs.length; j++) {if (matrix[i][j]!=INF){edges[index++] = new EData(vertexs[i],vertexs[j],matrix[i][j]);}}}return edges;}/*** 获取下标为i的顶点的终点()，用于后面判断两个顶点的终点是否相同* @param ends 记录了各个顶点对应的终点是哪个，在遍历过程中逐步生成* @param i 传入的顶点对应的下标* @return 下标为i的这个顶点对应的终点的下标*/private int getEnd(int[] ends,int i){while (ends[i]!=0){i = ends[i];//有终点返回终点}return i;//未加入包含这个顶点的边，理解为终点是自己}
}//创建一个EData,它的对象实例就表示一条边
class EData{char start; //边的一个点（起点）char end;//边的另一点（终点）int weight;//边的权//构造器public EData(char start, char end, int weight) {this.start = start;this.end = end;this.weight = weight;}//重写toString,便于输出边@Overridepublic String toString() {return "EData{" +"<" + start +"," + end +"> = " + weight +'}';}
}

---

关注我，共同进步，每周至少一更。——Wayne