Java数据结构之稀疏数组

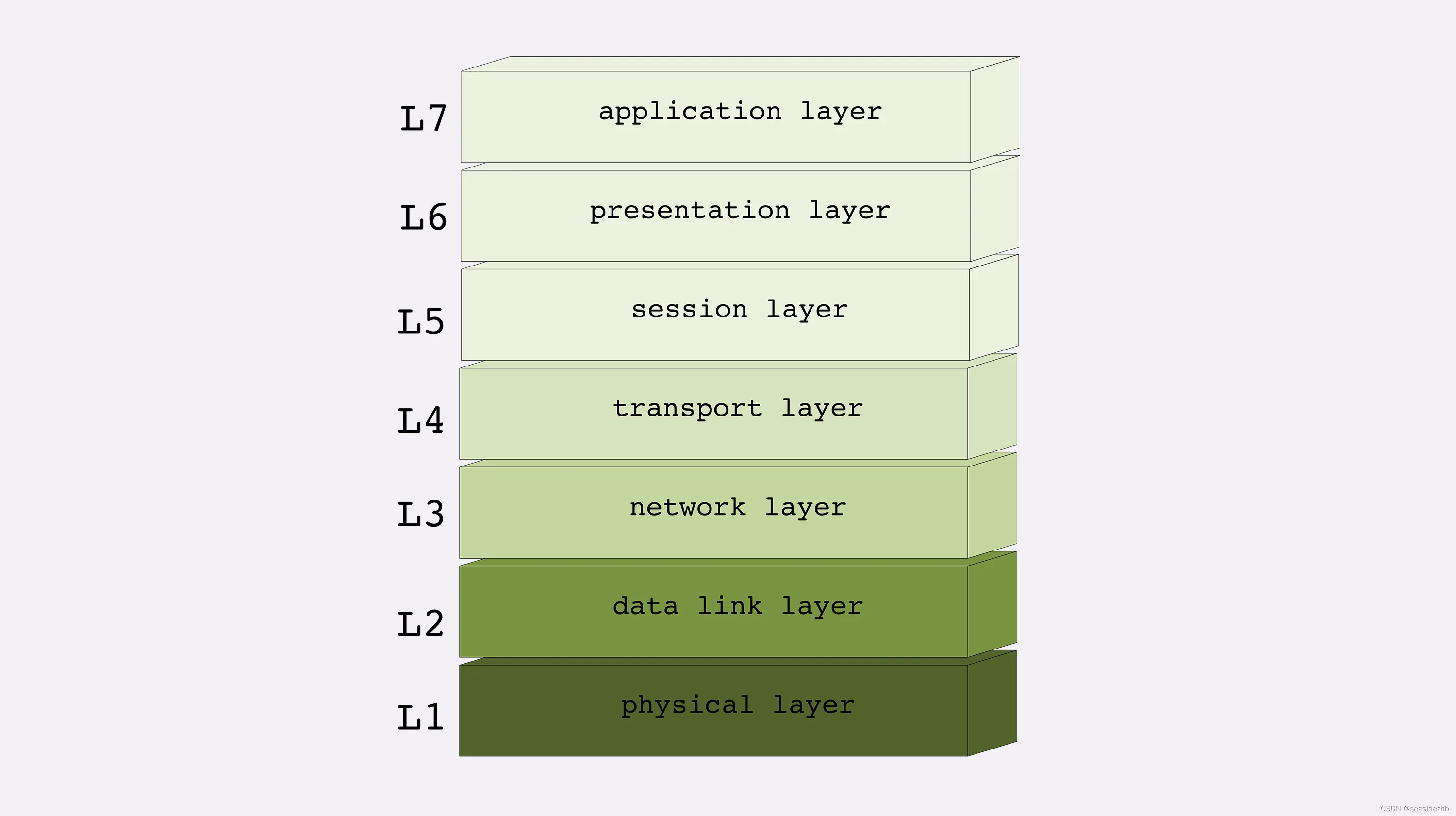
线性结构与非线性结构

线性结构

数据结构分两种，线性与非线性，线性结构的数据元素之间存在一对一的关系。

一对一指的是每个数据元素都有且仅有一个前驱元素和一个后继元素。元素之间存在严格顺序关系，每个元素都与唯一的一个元素相邻，一个元素的前一个元素就是它的前驱元素，后一个元素就是它的后继元素。确保元素在结构中的排列顺序。

举例来说，如果你有一个线性表（如数组或链表）包含整数元素 [1, 2, 3, 4, 5]，那么元素1的前驱是空，后继是2；元素2的前驱是1，后继是3；元素3的前驱是2，后继是4。依此类推。

一对一的关系区分了线性结构与其他数据结构，如树或图，这些数据结构的元素之间可以有多个连接或关系。

关于线性结构的存储方式有两种，顺序存储与链式存储。

顺序存储（Sequential Storage）： 线性结构的元素被存储在内存中一系列连续的存储单元中。这通常涉及使用数组来实现。每个元素都占用固定大小的内存空间，可以通过索引来访问元素。顺序存储适用于静态数据结构，元素的个数不会频繁地发生变化，因为插入或删除元素可能需要移动其他元素，效率较低。

举例：静态数组（如 Java 中的 int[]）是一种顺序存储的线性结构。
链式存储（Linked Storage）： 在链式存储中，线性结构的元素不一定是连续存储的，而是通过指针或引用相互连接在一起。每个元素通常包含数据和指向下一个元素的指针（或引用）。链式存储适用于动态数据结构，元素的插入和删除操作较为高效，因为不需要移动其他元素。

举例：链表是一种典型的链式存储的线性结构，包括单向链表、双向链表和循环链表等。

以下是一些常见的线性结构：

数组（Array）： 数组是一种最基本的线性结构，其中元素在内存中按顺序连续存储。数组的大小通常是固定的，但在一些编程语言中也可以动态调整。数组允许随机访问元素，因为可以通过索引快速访问任何元素。
链表（Linked List）： 链表是一种基于链式存储的线性结构，它由节点组成，每个节点包含数据和指向下一个节点的指针。链表分为单向链表、双向链表和循环链表等类型，允许高效的插入和删除操作，但访问元素的效率相对较低。
栈（Stack）： 栈是一种特殊的线性结构，遵循后进先出（LIFO）原则。只能在栈顶进行插入（压栈）和删除（弹栈）操作，常用于表达式求值、递归函数调用和撤销功能等。
队列（Queue）： 队列是一种基于先进先出（FIFO）原则的线性结构。元素从队列的一端（队尾）插入，从另一端（队首）删除。队列常用于调度、任务管理和广度优先搜索等算法。
双端队列（Deque）： 双端队列是一种允许从两端插入和删除元素的线性结构，可以同时充当栈和队列的角色。
线性索引表（Index List）： 线性索引表包括线性表的基本结构，但具有额外的索引，使得可以更快速地查找和访问元素。
线性堆（Heap）： 堆是一种特殊的树状线性结构，通常分为最小堆和最大堆。堆被广泛用于实现优先队列和堆排序等算法。

这些线性结构在计算机科学和编程中都有广泛的应用，每种结构都适用于不同的问题和场景，根据需求选择合适的数据结构可以提高算法的效率和代码的可读性。

非线性结构

非线性结构是元素之间的关系不是一对一的，元素之间可以有多对多的关系，形成更为复杂的连接模式。这些结构通常不是基于单一直线的排列，而是呈现出分支或网状的结构。

一些常见的非线性结构包括：

树（Tree）： 由节点组成，每个节点可以有一个父节点和零个或多个子节点。树被广泛用于层次化数据的表示，例如文件系统、组织结构等。特殊的树包括二叉树、二叉搜索树、平衡树、红黑树等。
图（Graph）： 图是一种包含节点和边的非线性结构，节点之间的连接关系可以是多对多的，没有固定的层次结构。图用于表示各种复杂关系，如社交网络、网络拓扑、路线图等。特殊的图包括有向图、无向图、加权图、有向无环图（DAG）等。
堆（Heap）： 堆虽然通常被视为线性结构的一种，但它实际上也是非线性结构。堆是一种特殊的树状结构，用于实现优先队列和堆排序等算法。最小堆和最大堆是堆的常见变种。
多维数组： 多维数组可以被视为非线性结构，因为元素之间的关系不仅仅是线性的。例如，二维数组是一个具有行和列的非线性结构，元素通过两个索引进行访问。

非线性结构在解决复杂的问题和表示多样化的数据关系时非常有用，但它们通常比线性结构更复杂，因此在访问和操作上可能需要更多的计算资源和算法。选择合适的数据结构取决于问题的性质和需求。

稀疏数组

应用场景

玩五子棋游戏，会有一个存档的功能，如果将盘上的所有的点都存下来会影响性能，这个时候可以通过稀疏数组来压缩棋盘来存储对应的位置，精确记录非默认值元素的信息，以节省存储空间和处理效率。

稀疏数组SparseArray用于表示大多数元素值为相同默认值（通常是0有可能是其它的默认值）的数组。

稀疏数组通常由三个部分组成：

原始数组的大小：原始数组的行数和列数。
非默认值元素的个数及其位置信息：存储非默认值元素的值、行号和列号。
默认值：用于填充原始数组中未包含在稀疏数组中的位置。

虽然稀疏数组可以用于表示稀疏矩阵等多维数据，但稀疏数组本身的元素存储通常是线性的，这使得它可以有效地表示和压缩大规模的多维数据。

稀疏数组在许多应用中都有广泛的用途，特别是当处理大型数据集中存在大量默认值的情况时。以下是一些常见的应用场景：

图像处理： 在数字图像处理中，图像通常由像素组成，而大多数图像中的像素都具有相同的默认颜色或灰度值。使用稀疏数组可以有效地表示图像，只存储非默认像素的颜色值。
文本处理： 文本文档中通常包含大量空白字符，对于稀疏文本，可以使用稀疏数组来存储文本内容，减少存储空间的需求。
稀疏矩阵： 在科学和工程领域，许多矩阵都是稀疏的，其中大多数元素为零。这种情况下，稀疏数组可以用于表示和处理这些矩阵，减少内存和计算资源的开销。例如，在有限元分析、线性代数和网络分析中经常使用稀疏矩阵。
地理信息系统（GIS）： GIS 数据通常包括地理坐标点，但大部分地理空间中没有点数据。使用稀疏数组可以有效地存储地理坐标信息，减小数据文件的大小。
网络路由表： 在计算机网络中，路由表用于指导数据包的传输。由于互联网规模庞大，网络路由表往往是稀疏的，其中只有少数路由条目被激活。稀疏数组可以用于高效表示和检索路由信息。
机器学习和数据挖掘： 在某些机器学习和数据挖掘应用中，特征矩阵可能具有大量的零值。稀疏数组用于存储特征矩阵，以减小内存占用和加速算法执行。
数据库管理系统： 在数据库中，可以使用稀疏数组来表示具有大量空值或默认值的数据，以减小存储和查询开销。

这些场景中，稀疏数组可以显著减少存储和处理成本，提高效率，并帮助管理大规模数据集。因此，稀疏数组是许多数据处理和存储应用中的重要工具。

代码实现

根据下图，将对应的原始二维数组与稀疏数组的互相转换。
在这里插入图片描述

二维数组转稀疏数组

主要思路就是确定有效数据的个数，根据有效个数初始化稀疏数组，遍历原来的二维数组给稀疏数组赋值。以下是实现方法以及抽出了一个公共的方法。

package com.jektong.al.sparsearray;import java.util.Arrays;/*** 稀疏数组** @author jektong* @date 2023年10月19日 8:29*/
public class SparseArray {public static void main(String[] args) {// 构建出二维数组的模型int[][] sourceArray = new int[6][7];sourceArray[0][3] = 22;sourceArray[0][6] = 15;sourceArray[1][1] = 11;sourceArray[1][5] = 17;sourceArray[2][3] = -6;sourceArray[3][5] = 39;sourceArray[4][0] = 91;sourceArray[5][2] = 28;// 输出二维数组for (int[] ints : sourceArray) {for (int anInt : ints) {System.out.printf("%d\t", anInt);}System.out.println();}// 统计二维数组的有效数据个数 sum=8int sum = sum(sourceArray);// 根据长度定义稀疏数组,+1是因为第一行的放的是原始的数组的几行几列一共存多少数字int[][] spareArray = new int[sum + 1][3];// 给第一行赋值 [6 7 8] 6行7列8个数字spareArray[0][0] = 6;spareArray[0][1] = 7;spareArray[0][2] = sum;// 用一个计数位置来累加每个稀疏数组的行数int count = 0;// 给稀疏数组进行赋值for (int i = 0; i < 6; i++) {for (int j = 0; j < 7; j++) {// 不为0就开始赋值if (sourceArray[i][j] != 0) {count++;// 稀疏数组某行的第一个数 对应原来数组的行号索引spareArray[count][0] = i;// 稀疏数组某行的第二个数 对应原来数组的列号索引spareArray[count][1] = j;// 稀疏数组某行的第三个数 对应原来数组的元素值spareArray[count][2] = sourceArray[i][j];}}}// 遍历出稀疏数组for (int[] ints : spareArray) {for (int anInt : ints) {System.out.printf("%d\t", anInt);}System.out.println();}// convertSpareArray(sourceArray);}/*** 统计二维数组的有效数据个数*/public static int sum(int[][] array) {int sum = 0;for (int[] ints : array) {System.out.println(Arrays.toString(array[0]));// array[0]相当于表示第一行的列的个数for (int j = 0; j < array[0].length; j++) {if (ints[j] != 0) {sum++;}}}return sum;}/*** 将原来数组转为稀疏数组 这是一个公共方法** @param sourceArray 原始数组*/public static void convertSpareArray(int[][] sourceArray) {// 输出二维数组for (int[] ints : sourceArray) {for (int anInt : ints) {System.out.printf("%d\t", anInt);}System.out.println();}// 统计二维数组的有效数据个数 sum=8int sum = sum(sourceArray);// 根据长度定义稀疏数组,+1是因为第一行的放的是原始的数组的几行几列一共存多少数字int[][] spareArray = new int[sum + 1][3];// 给第一行赋值 [6 7 8] 6行7列8个数字spareArray[0][0] = sourceArray.length;spareArray[0][1] = sourceArray[0].length;spareArray[0][2] = sum;// 给稀疏数组进行赋值int count = 0;for (int i = 0; i < sourceArray.length; i++) {for (int j = 0; j < sourceArray[0].length; j++) {if (sourceArray[i][j] != 0) {count++;spareArray[count][0] = i;spareArray[count][1] = j;spareArray[count][2] = sourceArray[i][j];}}}// 遍历出稀疏数组for (int[] ints : spareArray) {for (int anInt : ints) {System.out.printf("%d\t", anInt);}System.out.println();}}
}

通常稀疏数组是以三元组的形式表示，我们可以使用一个包含自定义对象的列表或数组来封装这个三元组的行，列，值。

package com.jektong.al.sparsearray;public class SparseArray {public static void main(String[] args) {// 构建出二维数组的模型int[][] sourceArray = new int[6][7];sourceArray[0][3] = 22;sourceArray[0][6] = 15;sourceArray[1][1] = 11;sourceArray[1][5] = 17;sourceArray[2][3] = -6;sourceArray[3][5] = 39;sourceArray[4][0] = 91;sourceArray[5][2] = 28;SparseElement[] sparseArray = convertSparseArray(sourceArray);printSparseArray(sparseArray);}public static class SparseElement {int row;int col;int value;public SparseElement(int row, int col, int value) {this.row = row;this.col = col;this.value = value;}}public static SparseElement[] convertSparseArray(int[][] sourceArray) {int numRows = sourceArray.length;int numCols = sourceArray[0].length;int sum = 0;// 计算有效数据个数for (int[] ints : sourceArray) {for (int j = 0; j < numCols; j++) {if (ints[j] != 0) {sum++;}}}// 创建稀疏数组SparseElement[] sparseArray = new SparseElement[sum + 1];sparseArray[0] = new SparseElement(numRows, numCols, sum);int count = 1;for (int i = 0; i < numRows; i++) {for (int j = 0; j < numCols; j++) {if (sourceArray[i][j] != 0) {sparseArray[count] = new SparseElement(i, j, sourceArray[i][j]);count++;}}}return sparseArray;}public static void printSparseArray(SparseElement[] sparseArray) {for (SparseElement element : sparseArray) {System.out.println(element.row + "\t" + element.col + "\t" + element.value);}}
}

运行效果：

在这里插入图片描述

稀疏数组转二维数组

稀疏数组转二维数组相对简单，先确定第一行，然后遍历剩下的行数对原始数组进行赋值：

package com.jektong.al.sparsearray;/*** @author jektong* @date 2023年10月20日 18:58*/
public class SpareArrayConvert {public static void convertArray(int[][] spareArray){// 先确定原始数组是几行几列？有多少的有效数字int row = spareArray[0][0];int col = spareArray[0][1];// 初始化原始数组int[][] sourceArray = new int[row][col];// 遍历剩下的数组长度for(int i = 1; i <spareArray.length;i++){// 赋值sourceArray[spareArray[i][0]][spareArray[i][1]] = spareArray[i][2];}for (int[] ints : sourceArray) {for (int anInt : ints) {System.out.printf("%d\t",anInt);}}}
}