A*
P1379华容道
问题是要从初始布局用最少的步骤到目标布局，每次只能动0周围的格子，就是华容道；
怎么用算法的思路解决？
状态压缩思路
每个数字就代表当前的状态，队列和map函数都记录的是当前的状态数，
描述一个状态有矩阵形式也有一个数形式
这里c[3][3]是描述状态的矩阵，n就是描述状态的数
这里是把n转化为矩阵形式，并且得到矩阵中0的位置，用f,g记录
执行交换操作无法在数中执行，比较抽象，所以是要转为矩阵，在矩阵里尝试交换，交换完后再转回数的形式进行存储，就是为了节约空间，ns是当前矩阵按当前遍历次序移动完后的结果，
如果在Map里没有出现，就是Map里没有这个数（这个状态），就意味着是新到的状态，由于是bfs,所以必定是到达这个状态的最小步数
#include<iostream>
#include<map>
#include<queue>
#include<algorithm>
#define ll long long//在这里看到一种很骚的操作：直接把int定义成long long；main函数用signed类型--麻麻再也不怕我忘开long long了！
using namespace std;
const ll dx[]={-1,0,0,1},dy[]={0,-1,1,0};//转移数组；
ll n;
int main()
{cin>>n;queue<ll> q;q.push(n);map<ll,ll> m;m[n]=0;while(!q.empty()){int u=q.front(); //初始状态入队列int c[3][3],f=0,g=0,n=u;q.pop();if(u==123804765)break;for(ll i=2;i>=0;i--)for(ll j=2;j>=0;j--){c[i][j]=n%10,n/=10;if(!c[i][j])f=i,g=j;}for(ll i=0;i<4;i++){ll nx=f+dx[i],ny=g+dy[i],ns=0;if(nx<0||ny<0||nx>2||ny>2)continue; //越界就不执行swap(c[nx][ny],c[f][g]);for(ll i=0;i<3;i++)for(ll j=0;j<3;j++)ns=ns*10+c[i][j];//矩阵转数列 if(!m.count(ns)){m[ns]=m[u]+1;//map去重的同时顺便统计到达这个状态所需的步数q.push(ns);}swap(c[nx][ny],c[f][g]);//状态复原}}cout<<m[123804765]<<endl; // map的下标直接用数列表示return 0;
}map
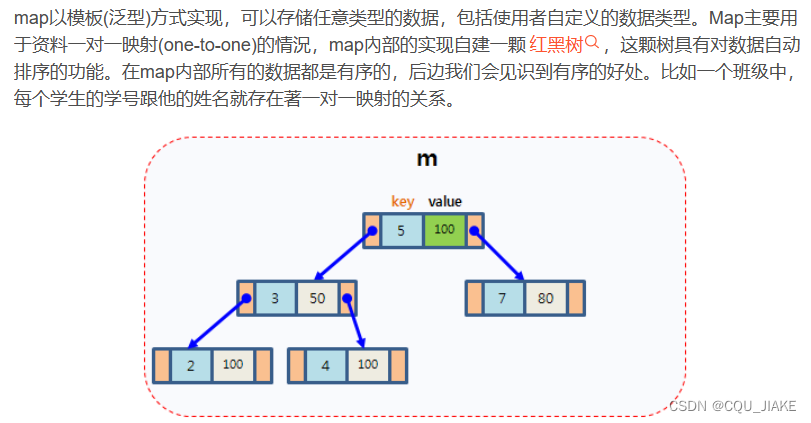
map查找
map操作函数
常用的count(),返回的是出现次数，int型，返回的是键的出现次数，不是键对应的值，所以只可能是0或者1
如果是!m.count(n)就表示是没有找到时触发，即此时map里还没有n这个键
m.count(n)就表示找到了这个元素，即map里此时已经有了n这个元素
A*方法
这一步是在判断当前状态是否还有可能是解，step是当前步数，cnt是估价函数值，cnt的值的确定，是有双重循环，一检测到当前格子里的和解里的不一样，就会++cnt,这循环9次，或者在循环里时就超过限制，就退出了
这个就是判断当前是不是解
就是说pre是记录上一次到这里来时的方向标号，就意味着不应该再走回去，如果走回去的话，就是先向上（下）走再向下（上）走，先向左（右）走再向右（左）走
可以人为定义状态移动数组，从而满足相反方向的序号具有一定关系
这里是使用对称数组排列，从而使相反方向的序号加和为数组长度-1
所以在递归判断中，是要判断pre+i==3,pre是上一个方向，i是这次选择的方向，加起来为3就是走了回去，需要被剪掉
这个操作虽然不能避免死循环的诞生，比如回字型循环，或者重复状态的出现（避免了只需两步的重复状态，但可能多步回到初始位置），但依然可以避免大量的两步重复
这里是将输入的字符串（状态压缩的序列）转为矩阵，并得到0的位置
是把K作为外层循环，即直接建立在步数限制的基础上判断当前是不是能到达
#include<iostream>
#include<string>
#include<map>
#include<cmath>
#include<algorithm>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long lt;int read()
{int f=1,x=0;char ss=getchar();while(ss<'0'||ss>'9'){if(ss=='-')f=-1;ss=getchar();}while(ss>='0'&&ss<='9'){x=x*10+ss-'0';ss=getchar();}return f*x;
}char ss[15];
int ans[4][4]=
{{0,0,0,0},{0,1,2,3},{0,8,0,4},{0,7,6,5}};
int a[5][5],k,judge;
int nxtx[]={0,1,-1,0};
int nxty[]={1,0,0,-1};int check()
{for(int i=1;i<=3;++i)for(int j=1;j<=3;++j)if(ans[i][j]!=a[i][j])return 0;return 1;
}int test(int step)
{int cnt=0;for(int i=1;i<=3;++i)for(int j=1;j<=3;++j)if(ans[i][j]!=a[i][j]){ if(++cnt+step>k) return 0;}return 1;
}void A_star(int step,int x,int y,int pre)
{if(step==k){ if(check())judge=1; return;}达到当前限制的最大深度if(judge) return;for(int i=0;i<4;++i){int nx=x+nxtx[i],ny=y+nxty[i];if(nx<1||nx>3||ny<1||ny>3||pre+i==3) continue;//加入了上述最优性剪枝swap(a[x][y],a[nx][ny]);if(test(step)&&!judge) A_star(step+1,nx,ny,i);//A*估价合法再向下搜索swap(a[x][y],a[nx][ny]);}
}int main()
{int x,y;scanf("%s",&ss);for(int i=0;i<9;++i){a[i/3+1][i%3+1]=ss[i]-'0';if(ss[i]-'0'==0)x=i/3+1,y=i%3+1;}if(check()){printf("0");return 0;}//特判不用移动while(++k)//枚举最大深度{A_star(0,x,y,-1);if(judge){printf("%d",k);break;}}return 0;
}
