文章目录
- 堆的简介
- 堆的实现
- 堆的插入数据
- 堆的删除数据
- 堆排序
- 向上调整和向下调整的时间复杂度的分析
- 大量数据的topk问题
堆的简介
今天要写的数据结构是堆,什么是堆呢?堆其实是一种完全二叉树,只不过它是有条件的。
堆分为两种,一种是大根堆,又叫大堆,顾名思义就是每棵子树的父亲节点都大于孩子节点,另一种是小根堆,又叫小堆,自然就是每颗子树的父亲节点都大于孩子节点。
堆一般在内存中是以数组的形式存储的,就是从根节点开始从上往下,从左往右依次存储,下面是一个大根堆的逻辑形式和物理中的存储形式。
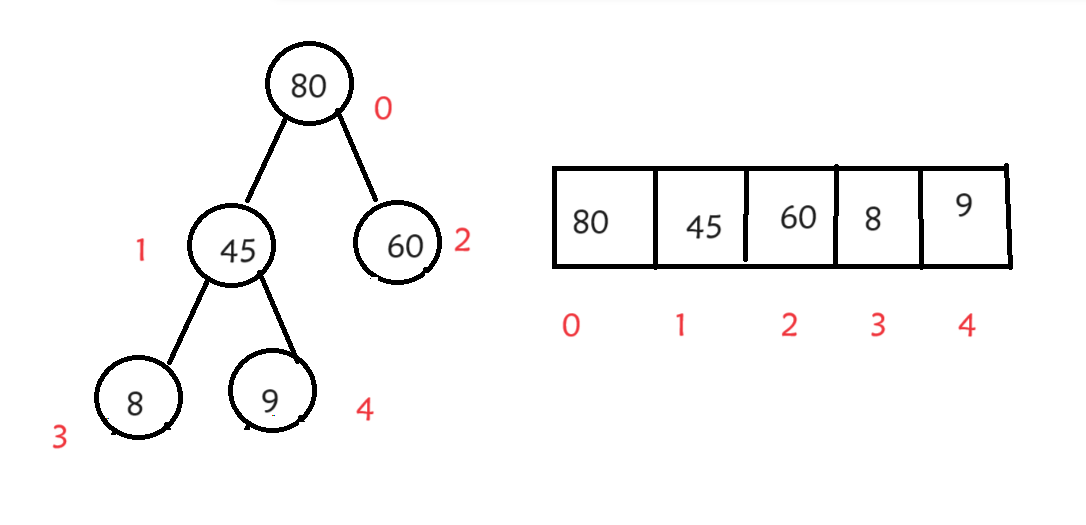
这个堆就满足我们上面说的条件,标红的是数组的下标。
不知道你有没有发现,每个父亲节点和它的孩子节点在下标上有一定的关系,左孩子=父亲*2+1,右孩子=父亲*2+2,你可以用图上的结点来试一下。
那么怎么通过孩子来找父亲呢?其实 孩子-1/2就是它的父亲节点,最简单的下标0 1 2来试一下,1和2减去1再除2就是0。
你可能会说这有什么作用呢?它结构相对与之前也变复杂了,那么自然,它解决问题的效率也就会更高,比如说我们冒泡排序的时间复杂度是O(N^2),但是我们后面要讲的堆排序的时间复杂度就是O(N*logN)。以及后面的topk问题都需要用到我们的堆,因为它处理起来确实是很方便的。
堆的实现
下面我们来实现一下这种数据结构
我们说过,堆是以数组的形式在内存中存储的,所以它的类型就类似于顺序表。
typedef int HPDataType;typedef struct Heap {HPDataType* a;int size;int capacity;
}HP;
初始化和销毁函数就非常的简单了,关键就是在于它里面的操作和顺序表是不一样的,下面我们来着重说一下它里面的操作是什么样的,怎么把一个无序的数组变成一个有一定顺序的堆。
堆的插入数据
下面就是关键的插入函数,我们可以一个元素一个元素的插入,当然也可以一下插入一整个数组,它们的核心关键不会变化,那就是调整这一步。什么意思呢?就是我们插入的话肯定是在数组尾部插入,之后再调整整个数组,让这个数组变成堆。那么问题来了,怎么调整成了关键。
以小根堆为例,当我们插入第一个数时,堆中就只有一个数据,那么它自然而然就是一个小根堆,从插入第二个数时,我们就要开始调整了。从后面插入东西,把它调到前面,我们叫做向上调整。
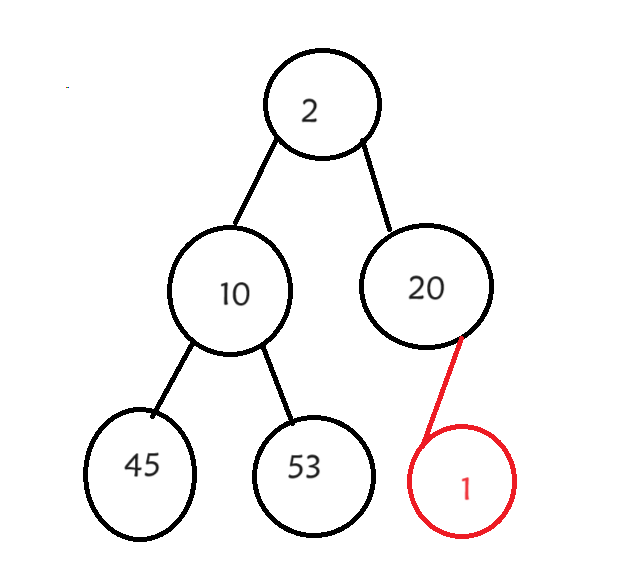
比如说我们要给20这个节点插入一个左孩子1
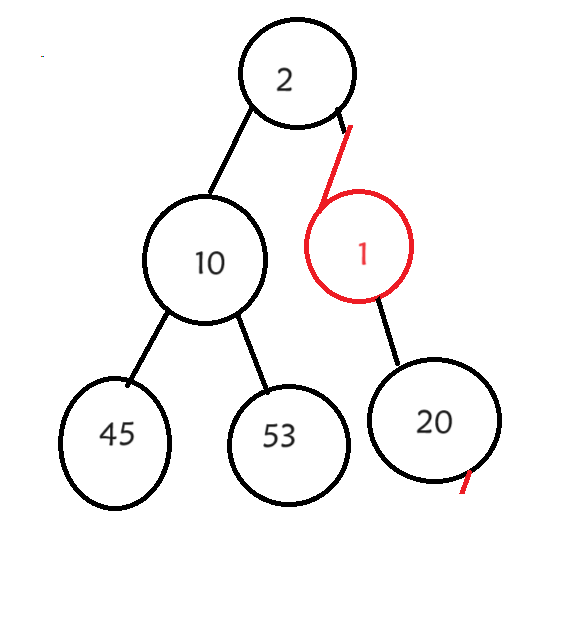
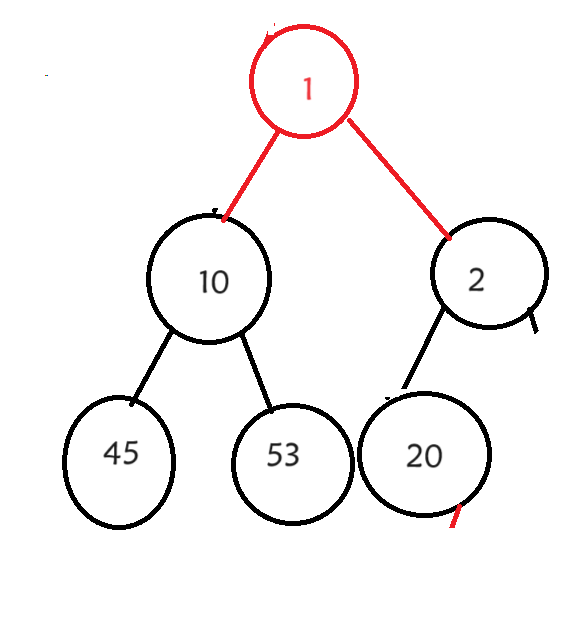
在插入1之前我们这是一个小根堆,那么我们现在要做的就是调整这个1的位置,让它重新形成一个小根堆。其实这个数值之间的大小关系只存在与父亲与孩子之间,兄弟之间并不存在这种关系,所以我们只需要调整父亲与孩子就可以了,孩子比父亲小就交换它们之间的位置,直到满足一个小根堆的条件为止。
它的调整的一个基本思想就是这样
下面是向上调整的一个函数
void AdjustUp(HPDataType* a, int child) {//child是要向上调整的数据的下标int parent = (child - 1) / 2;while (child > 0) {if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else {break;}}
}
有了这个函数,我们就可以实现堆的逐个数据插入了
void HeapPush(HP* php, HPDataType x) {assert(php);if (php->size == php->capacity) {//扩容int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (tmp == NULL) {perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;//数组末尾插入新数据php->size++;AdjustUp(php->a, php->size - 1);//将插入的数据向上调整
}
我们要实现整个数组去插入到一个堆中其实也一样,就先全部插入然后从第二个元素开始向上调整,直到全部调整完。
void HeapInitArray(HP* php, int* a, int n) {assert(php);assert(a);php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (php->a == NULL) {perror("malloc fail");exit(-1);}php->size = n;php->capacity = n;memcpy(php->a, a, sizeof(HPDataType) * n);for (int i = 1; i < n; i++) {AdjustUp(php->a, i);}
}
堆的删除数据
这里的删除呢其实不是正常意义上的删除,而是取出一个有意义的数据,这里以小根堆为例,它最有意义的数据是什么呢?当然就是它的根节点,因为它是这个队中最小的数据。比如说,topk问题,就是在一堆数据中去找到k个最大或最小的数据。
接下来我们说一下如何去取出根节点且让它还能保持成一个堆。就是让根节点和最后一个数据交换位置,在删掉最后一个位置,最后让根节点的数据向下调整,和向下调整在逻辑上向上调整是相反的,但实现方式都是差不多的,但是有一个区别,这里以小根堆为例,就是每一个父亲节点可能有两个孩子结点,要处理的父亲节点要跟小的结点交换,直到最后满足一个堆为止。
下面是向下调整函数
void AdjustDown(HPDataType* a, int n, int parent) {int child = parent * 2 + 1;while (child < n) {if (child + 1 < n && a[child + 1] < a[child]) {//为了找到兄弟节点中小的那个child++;}if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}
那么我们的删除函数也就很简单了
void HeapPop(HP* php) {assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}
堆排序
我们之所以创建堆,是因为它在某些方面确实是有一些优势的,下面是利用堆去实现排序功能
我们对一个数组去排序,可以先把这个数组调整成一个数据间关系与堆相同的样子,之后再往外取出数据,因为取出的话取出的就是极值
并且,排升序要建大根堆,排降序要建小根堆。
为什么呢?我们以排升序为例,建大根堆,因为根节点肯定是最大的元素,把根节点和最后一个节点交换位置,就排好最大的这个元素了,之后同理再排前几个元素就可以了。
下面用代码来实现一下
void my_heap_sort(int* a, int n)
{for (int i = 1; i < n; i++) {//类似于建造堆AdjustUp(a, i);}for (int i = n - 1; i > 0; i--) {Swap(&a[i], &a[0]);AdjustDown(a, i, 0);}
}
int main() {int a[] = { 45,12,7,9,13,62,96,17,100,46,23,85 };my_heap_sort(a, sizeof(a) / sizeof(a[0]));for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++) {printf("%d ", a[i]);}return 0;
}
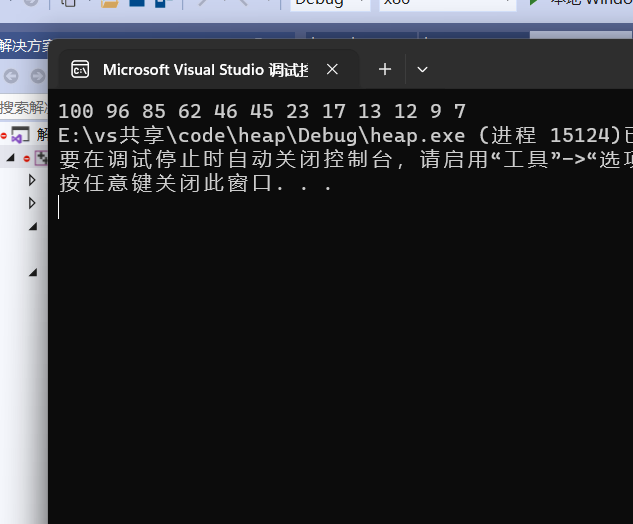
它就很容易的完成了排序功能,它的时间复杂度就是O(N*logN),确实比之前学的冒泡排序要高效一些
但是有个问题,我们在写这个堆排序的时候还要写两个函数,确实比较麻烦,其实我们可以只用向下调整的。
还是那个原理,叶子节点单拿出来是没有什么关系的,所以向下调整的话,只需要倒着从最后一个父亲节点开始向下调整就可以了,直到根节点也调整完。
所以说,可以只用向下调整,就是把上面代码的建堆过程改成下面的就可以了
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {AdjustDown(a, n, i);}
那么问题又来了,怎么找到最后一个父亲节点呢?其实最后一个叶子的父亲不就是最后一个父亲节点吗?所以这个代码中i的初始值是这样解释的,i-1是最后一个数据的下标,用这个下标减一除二就是它的父亲节点。
向上调整和向下调整的时间复杂度的分析
我们来计算一下一个高度为h的完全二叉树从全乱到成为一个堆(每个结点都是最坏情况)需要调整多少步
先看小根堆
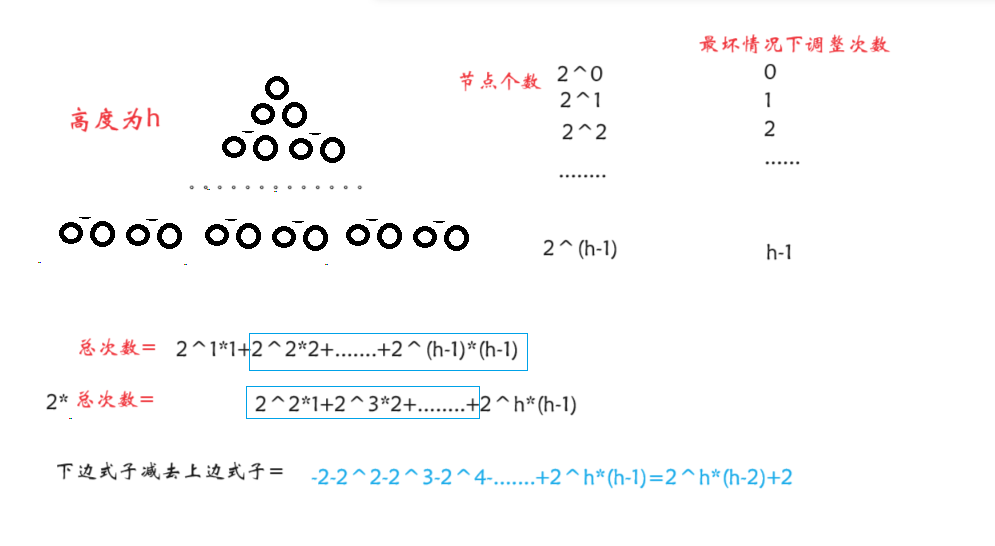
再看大根堆
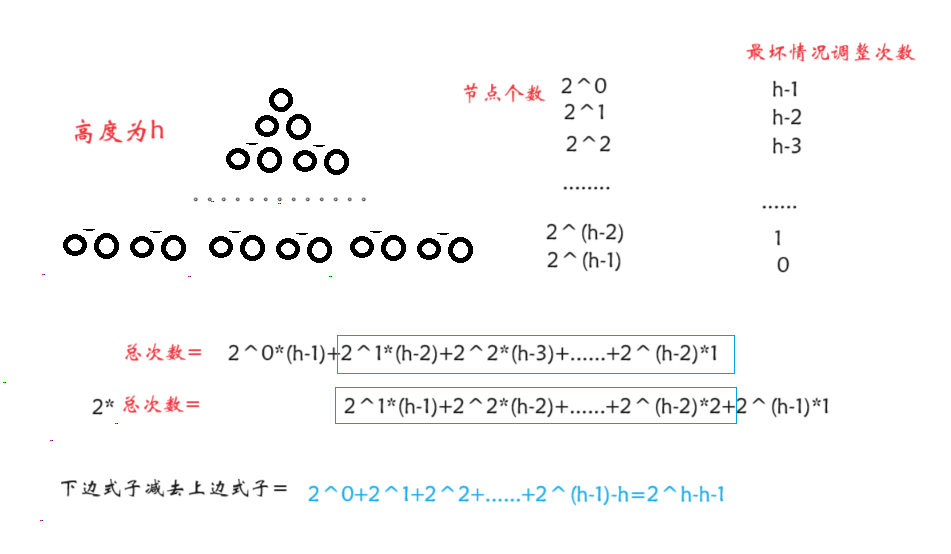
可以发现它们不是一个数量级,看大根堆,2的h次方个数据大概要调整2的h次方次,所以时间复杂度为O(N),同理,小根堆的时间复杂度为O(N*logN)
大量数据的topk问题
有时候我们要处理的问题有很多,多到不能在内存中处理,我们必须得把数据放到文件中,那么这时我们应该如何处理topk问题呢?
首先我们创建一个函数,用来在文件中放入一百万个随机数据,当然这些数据都要小于一个值,我们设置为一百万,然后再去文件中随机更改五个数据,让这五个数据大于一百万,如果能成功找到这五个数据的话,那么我们的操作就成功了
有不会文件操作的可以去看我的另外一篇博客,链接如下:
链接:文件操作
void CreateNData() {int n = 1000000;srand((unsigned int)time(NULL));FILE* fin = fopen("data.txt", "w");if (fin == NULL) {perror("fopen error");return;}for (int i = 0; i < n; i++) {int x = (int)(((double)rand() / RAND_MAX) * 1000000);//这里产生的值小于一百万fprintf(fin,"%d\n", x);}fclose(fin);fin = NULL;
}
之后我们在这个data.txt的文件中就随机产生了一百万个数据,这里一百万个数据都小于一百万,因为RAND_MAX是32767,所以我们可以用上面的方法使产生的数据小于一百万
之后我们随机改k个数,让这k个数大于一百万,让程序去找
怎么找呢?我们比如说要找十个数,然后我们创建一个能存放十个数的堆,先把文件中前十个数据放入堆中并排序成一个小根堆,根节点那个值肯定是最小的,后面的数据中有大于根节点的就交换,并重新形成一个堆,最后留下的就是最大的十个数
void PrintTopK(const char* filename, int k) {FILE* fout = fopen(filename, "r");if (fout == NULL) {perror("fopen fail");return;}int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL) {perror("malloc fail");return;}for (int i = 0; i < k; i++) {fscanf(fout,"%d", &minheap[i]);}for (int i = (k - 2) / 2; i >= 0; i--) {AdjustDown(minheap, k, i);}int x = 0;while (fscanf(fout, "%d", &x) != EOF) {if (x > minheap[0]) {minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++) {printf("%d ", minheap[i]);}printf("\n");free(minheap);fclose(fout);
}
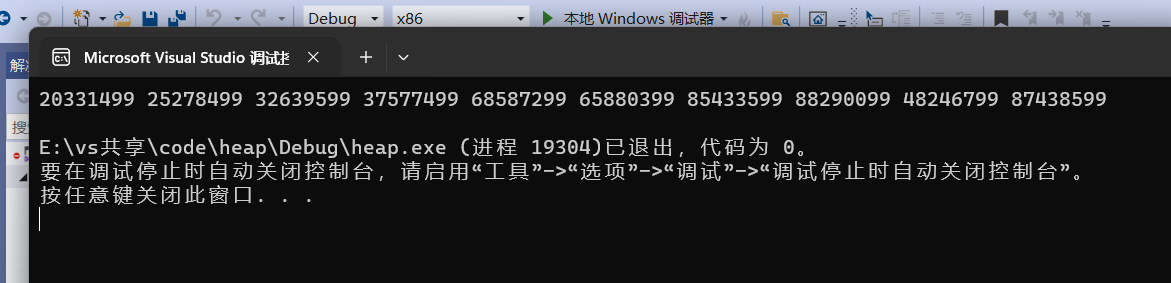
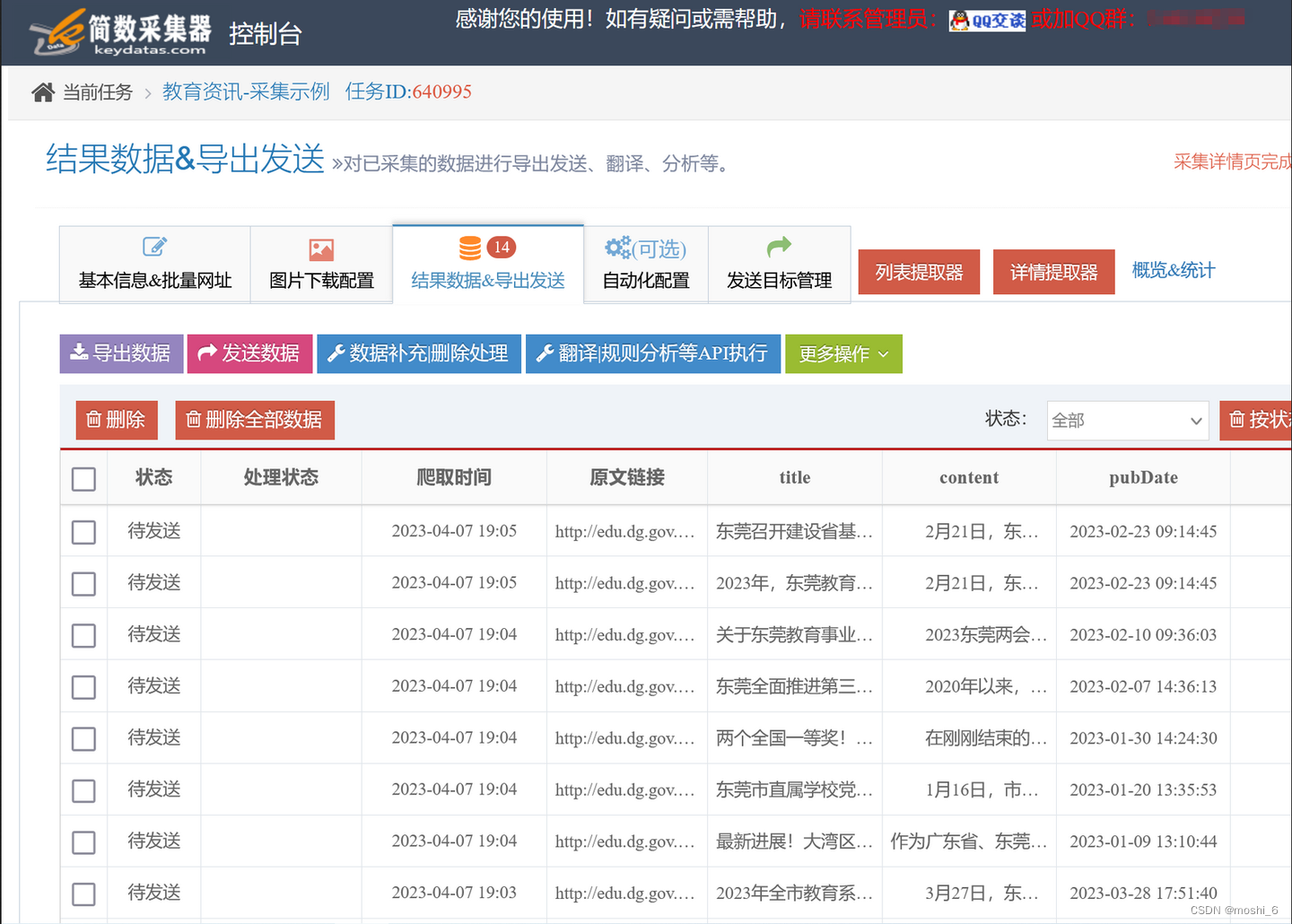
它也是成功找到了我埋藏的这十个最大的数了
![[Ubuntu 18.04] 搭建文件夹共享之Samba服务器](https://img-blog.csdnimg.cn/f0fd09f6eead4bf5b2116fb3578069fb.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBATmV1dGlvbndlaQ==,size_20,color_FFFFFF,t_70,g_se,x_16)
![[数据分析与可视化] 基于Python绘制简单动图](https://img-blog.csdnimg.cn/img_convert/109d834890f04c38ce7e4597759ea39a.gif)