一、特征工程

特征工程（Feature Engineering）对特征进行进一步分析，并对数据进行处理。
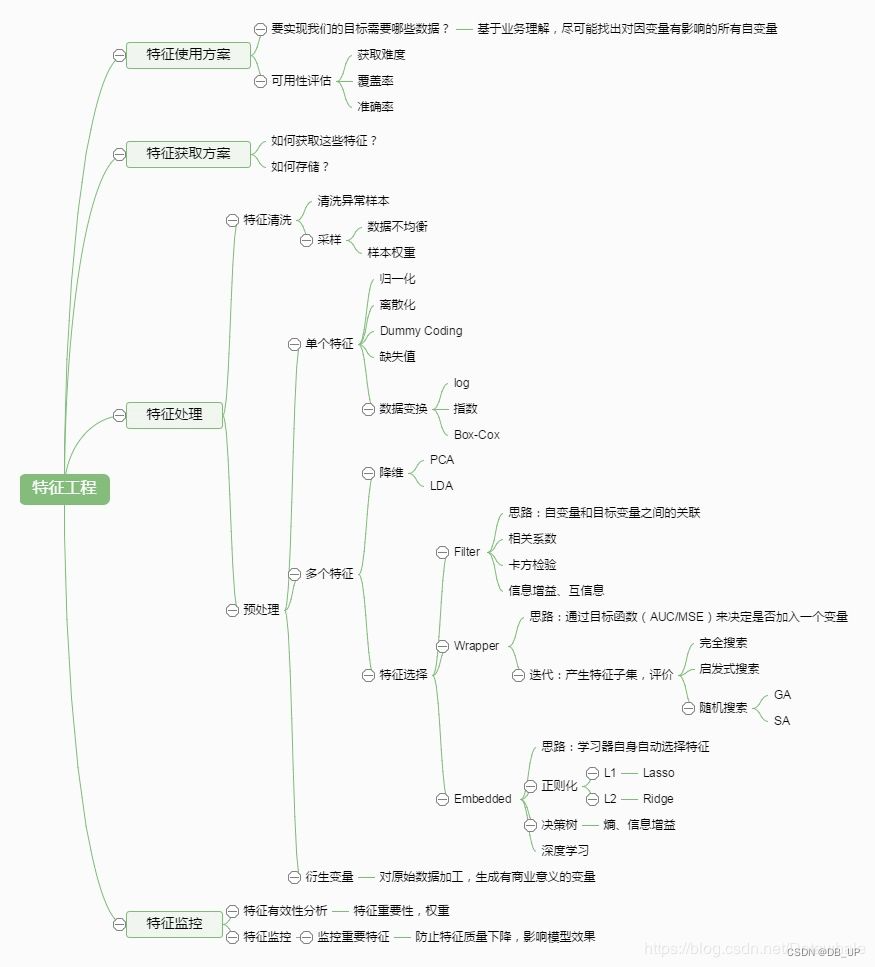
常见的特征工程包括：异常值处理、缺失值处理、数据分桶、特征处理、特征构造、特征筛选及降维等。

1、异常值处理

'''具体实现'''
from scipy.stats import boxcox
boxcox_transformed_data = boxcox(original_data)

1.1 箱线图

箱线图筛选异常并进行截尾，这里不用删除，其原因为：
1、笔者已经合并了训练集和测试集，若删除的话，肯定会删除测试集的数据
2、删除有时候会改变数据的分布等

"""这里包装了一个异常值处理的代码，可以随便调用"""
def outliers_proc(data, col_name, scale=3):   """ 用于截尾异常值， 默认用box_plot(scale=3)进行清洗   param:            data：接收pandas数据格式           col_name: pandas列名         scale: 尺度    """    data_col = data[col_name]    Q1 = data_col.quantile(0.25) # 0.25分位数  Q3 = data_col.quantile(0.75)  # 0.75分位数   IQR = Q3 - Q1data_col[data_col < Q1 - (scale * IQR)] = Q1 - (scale * IQR)    data_col[data_col > Q3 + (scale * IQR)] = Q3 + (scale * IQR)return data[col_name]
num_data['power'] = outliers_proc(num_data, 'power')

1.2 缺失值

关于缺失值处理的方式，有几种情况：
1、不处理（这是针对xgboost等树模型），有些模型有处理缺失的机制，所以可以不处理
2、如果缺失的太多，可以考虑删除该列
3、插值补全（均值，中位数，众数，建模预测，多重插补等）
4、分箱处理，缺失值一个箱。

''' 删除重复值'''
data.drop_duplicates()
dropna()可以直接删除缺失样本，但是有点不太好
'''填充固定值'''
train_data.fillna(0, inplace=True) # 填充 0
data.fillna({0:1000, 1:100, 2:0, 4:5})   # 可以使用字典的形式为不用列设定不同的填充值
train_data.fillna(train_data.mean(),inplace=True) # 填充均值
train_data.fillna(train_data.median(),inplace=True) # 填充中位数
train_data.fillna(train_data.mode(),inplace=True) # 填充众数
train_data.fillna(method='pad', inplace=True) # 填充前一条数据的值，但是前一条也不一定有值
train_data.fillna(method='bfill', inplace=True) # 填充后一条数据的值，但是后一条也不一定有值
'''插值法：用插值法拟合出缺失的数据，然后进行填充'''
for f in features:     train_data[f] = train_data[f].interpolate()
train_data.dropna(inplace=True)
'''填充KNN数据：先利用knn计算临近的k个数据，然后填充他们的均值'''
from fancyimpute import KNN
train_data_x = pd.DataFrame(KNN(k=6).fit_transform(train_data_x), columns=features)

1.3 数据分桶

连续值经常离散化或者分离成“箱子”进行分析，为什么要做数据分桶呢？·离散后稀疏向量内积乘法运算速度更快，计算结果也方便存储，容易扩展；
1、离散后的特征对异常值更具鲁棒性，如age>30为1否则为0，对于年龄为200的也不会对模型造成很大的干扰；
2、LR属于广义线性模型，表达能力有限，经过离散化后，每个变量有单独的权重，这相当于引入了非线性，能够提升模型的表达能力，加大拟合；
3、离散后特征可以进行特征交叉，提升表达能力，由M+N个变量编程M*N个变量，进一步引入非线形，提升了表达能力；
4、特征离散后模型更稳定，如用户年龄区间，不会因为用户年龄长了一岁就变化当然还有很多原因，LightGBM在改进XGBoost时就增加了数据分桶，增强了模型的泛化性。
现在介绍数据分桶的方式：
等频分桶
等距分桶
Best-KS分桶（类似利用基尼指数进行二分类）
卡方分桶
最好将数据分桶的特征作为新一列的特征，不要把原来的数据给替换掉，所以在这里通过分桶的方式做一个特征出来看看，以power为例：

"""下面以power为例进行分桶， 当然构造一列新特征了"""
bin = [i*10 for i in range(31)]
num_data['power_bin'] = pd.cut(num_data['power'],bin,labels=False)

当然这里的新特征会有缺失。这里也放一个数据分桶的其他例子（迁移之用）

# 连续值经常离散化或者分离成“箱子”进行分析。
# 假设某项研究中一组人群的数据，想将他们进行分组，放入离散的年龄框中
ages = [20, 22, 25, 27, 21, 23, 37, 31, 61, 45, 41, 32]
# 如果按年龄分成18-25, 26-35, 36-60, 61以上的若干组，可以使用pandas中的cut
bins = [18, 25, 35, 60, 100]         # 定义箱子的边
cats = pd.cut(ages, bins)
print(cats)   # 这是个categories对象  通过bin分成了四个区间,然后返回每个年龄属于哪个区间
# codes属性
print(cats.codes)    #  这里返回一个数组，指明每一个年龄属于哪个区间
print(cats.categories)
print(pd.value_counts(cats))   # 返回结果是每个区间年龄的个数
# 与区间的数学符号一致， 小括号表示开放，中括号表示封闭， 可以通过right参数改变
print(pd.cut(ages, bins, right=False))
# 可以通过labels自定义箱名或者区间名
group_names = ['Youth', 'YonngAdult', 'MiddleAged', 'Senior']
data = pd.cut(ages, bins, labels=group_names)
print(data)
print(pd.value_counts(data))
# 如果将箱子的边替代为箱子的个数，pandas将根据数据中的最小值和最大值计算出等长的箱子
data2 = np.random.rand(20)
print(pd.cut(data2, 4, precision=2))   # precision=2 将十进制精度限制在2位
#qcut是另一个分箱相关的函数,基于样本分位数进行分箱。取决于数据的分布,使用cut不会使每个箱子
具有相同数据数量的数据点，而qcut,使用样本的分位数,可以获得等长的箱
data3 = np.random.randn(1000)   # 正态分布
cats = pd.qcut(data3, 4)
print(pd.value_counts(cats))

1.4 数据转换

数据转换的方式有：
数据归一化（Min MaxScaler）
标准化（StandardScaler）
对数变换（log1p）
转换数据类型（astype）
独热编码（OneHotEncoder）
标签编码（LabelEncoder）
修复偏斜特征（boxcox1p）
1.数值特征归一化，因为这里数值的取值范围相差很大

minmax = MinMaxScaler()
num_data_minmax = minmax.fit_transform(num_data)
num_data_minmax = pd.DataFrame(num_data_minmax, columns=num_data.columns, index=num_data.index)

2.类别特征独热一下

"""类别特征某些需要独热编码一下"""
hot_features = ['bodyType', 'fuelType', 'gearbox', 'notRepairedDamage']
cat_data_hot = pd.get_dummies(cat_data, columns=hot_features)

3.关于高势集特征model，也就是类别中取值个数非常多的，一般可以使用聚类的方式，然后独热，这里就采用了这种方式：

from scipy.cluster.hierarchy import linkage, dendrogram
from sklearn.cluster import AgglomerativeClustering
from sklearn.cluster import KMeans
ac = KMeans(n_clusters=3)
ac.fit(model_price_data)
model_fea = ac.predict(model_price_data)
plt.scatter(model_price_data[:,0],model_price_data[:,1],c=model_fea)
cat_data_hot['model_fea'] = model_fea
cat_data_hot = pd.get_dummies(cat_data_hot, columns=['model_fea'])

1.5 特征构造

在特征构造的时候，需要借助一些背景知识，遵循的一般原则就是需要发挥想象力，尽可能多的创造特征，不用先考虑哪些特征可能好，可能不好，先弥补这个广度。特征构造的时候需要考虑数值特征，类别特征，时间特征。
对于数值特征，一般会尝试一些它们之间的加减组合（当然不要乱来，根据特征表达的含义）或者提取一些统计特征
对于类别特征，我们一般会尝试之间的交叉组合，embedding也是一种思路(将离散变量转变为连续向量)
对于时间特征，这一块又可以作为一个大专题来学习，在时间序列的预测中这一块非常重要，也会非常复杂，需要就尽可能多的挖掘时间信息，会有不同的方式技巧。当然在这个比赛中涉及的实际序列数据有一点点，不会那么复杂。
eg:

1、时间特征的构造
根据上面的分析，可以构造的时间特征如下：
（1）汽车的上线日期与汽车的注册日期之差就是汽车的使用时间，一般来说与价格成反比
（2）对汽车的使用时间进行分箱，使用了3年以下，3-7年，7-10年和10年以上，分为四个等级，10年之后就是报废车了，应该会影响价格
（3）淡旺季也会影响价格，所以可以从汽车的上线日期上提取一下淡旺季信息
汽车的使用特征
createDate-regDate，反应汽车使用时间，一般来说与价格成反比。但要注意的问题就是时间格式，regDateFalse这个字段有些是0月，如果忽略错误计算的话，使用时间有一些会是空值，当然可以考虑删除这些空值，但是因为训练集和测试集合并了，那么就不轻易删除了。
本文采取的办法是把错误字段都给他加1个月，然后计算出天数之后在加上30天（这个有不同的处理方式，但是一般不喜欢删除或者置为空，因为删除和空值都有潜在的副作用）

# 这里是为了标记一下哪些字段有错误
def regDateFalse(x):    if str(x)[4:6] == '00':        return 1    else:         return 0
time_data['regDateFalse'] = time_data['regDate'].apply(lambda x: regDateFalse(x))
# 这里是改正错误字段
def changeFalse(x):    x = str(x)    if x[4:6] == '00':        x = x[0:4] + '01' + x[6:]       x = int(x)   return x
time_data['regDate'] = time_data['regDate'].apply(lambda x: changeFalse(x))
# 使用时间：data['creatDate'] - data['regDate']，反应汽车使用时间，一般来说价格与使用时间成反比
# 不过要注意，数据里有时间出错的格式，所以我们需要 errors='coerce'
time_data['used_time'] = (pd.to_datetime(time_data['creatDate'], format='%Y%m%d')-pd.to_datetime(time_data['regDate'], format='%Y%m%d')).dt.days
# 修改错误# 但是需要加上那一个月
time_data.loc[time_data.regDateFalse==1, 'used_time'] += 30
# 删除标记列
del time_data['regDateFalse']

汽车是不是符合报废
时间特征还可以继续提取，我们假设用了10年的车作为报废车的话，那么我们可以根据使用天数计算出年数，然后根据年数构造出一个特征是不是报废。

# 使用时间换成年来表示time_data['used_time'] = time_data['used_time'] / 365.0
time_data['Is_scrap'] = time_data['used_time'].apply(lambda x: 1 if x>=10 else 0)

我们还可以对used_time进行分箱，这个是根据背景估价的方法可以发现，汽车的使用时间3年，3-7年，10年以上的估价会有不同，所以分一下箱。

bins = [0, 3, 7, 10, 20, 30]
time_data['estivalue'] = pd.cut(time_data['used_time'], bins, labels=False)

这样就又构造了两个时间特征。ls_scrap表示是否报废，estivalue表示使用时间的分箱。
是不是淡旺季
这个是根据汽车的上线售卖时间看，每年的2，3月份及6，7，8月份是整个汽车行业的低谷，年初和年末及9月份是二手车销售的黄金时期，所以根据上线时间选出淡旺季。

# 选出淡旺季
low_seasons = ['3', '6', '7', '8']
time_data['is_low_seasons'] = time_data['creatDate'].apply(lambda x: 1 if str(x)[5] in low_seasons else 0)
# 独热一下
time_data = pd.get_dummies(time_data, columns=['is_low_seasons'])
# 这样时间特征构造完毕，删除日期了
del time_data['regDate']
del time_data['creatDate']

根据汽车的使用时间或者淡旺季分桶进行统计特征的构造

# 构造统计特征的话需要在训练集上先计算
train_data_timestats = train_data.copy()   # 不要动train_data
train_data_timestats['estivalue'] = time_data['estivalue'][:train_data.shape[0]]
train_data_timestats['price'] = train_target
train_gt = train_data_timestats.groupby('estivalue')
all_info = {}
for kind, kind_data in train_gt:    info = {}    kind_data = kind_data[kind_data['price'] > 0]    info['estivalue_count'] = len(kind_data)    info['estivalue_price_max'] = kind_data.price.max()    info['estivalue_price_median'] = kind_data.price.median()    info['estivalue_price_min'] = kind_data.price.min()    info['estivalue_price_sum'] = kind_data.price.sum()    info['estivalueprice_std'] = kind_data.price.std()    info['estivalue_price_average'] = round(kind_data.price.sum() / (len(kind_data) + 1), 2)    all_info[kind] = info
estivalue_fe = pd.DataFrame(all_info).T.reset_index().rename(columns={"index": "estivalue"})
time_data = time_data.merge(estivalue_fe,how='left', on='estivalue')

类别特征的构造
经过上面的分析，可以构造的类别特征如下：
1、从邮编中提取城市信息，因为是德国的数据，所以参考德国的邮编，加入先验知识，但是感觉这个没有用，可以先试一下
2、最好是从regioncode中提取出是不是华东地区，因为华东地区是二手车交易的主要地区（这个没弄出来，不知道这些编码到底指的哪跟哪）
3、私用车和商用车分开（body Type提取）
4、是不是微型车单独处理，所以感觉那些车的类型OneHot的时候有点分散了（bodyType这个提取，然后one-hot）
5、新能源车和燃油车分开（在fuelType中提取，然后进行OneHot）
6、地区编码还是有影响的，不同的地区汽车的保率不同
7、品牌这块可以提取一些统计量，统计特征的话上面这些新构造的特征其实也可以提取注意，OneHot不要太早，否则有些特征就没法提取潜在信息了。
邮编特征
从邮编中提取城市信息，因为是德国的数据，所以参考德国的邮编，加入先验知识。

cat_data['city'] = cat_data['regionCode'].apply(lambda x: str(x)[0])

私用车和商务车分开（bodyType）

com_car = [2.0, 3.0, 6.0]  # 商用车
GL_car = [0.0, 4.0, 5.0]   # 豪华系列  
self_car = [1.0, 7.0]
def class_bodyType(x):   if x in GL_car:       return 0    elif x in com_car:        return 1    else:        return 2
cat_data['car_class'] = cat_data['bodyType'].apply(lambda x : class_bodyType(x))

新能源车和燃油车分开（fuelType）

# 是否是新能源
is_fuel = [0.0, 1.0, 2.0, 3.0]
cat_data['is_fuel'] = cat_data['fuelType'].apply(lambda x: 1 if x in is_fuel else 0)

构造统计特征
这一块依然是可以构造很多统计特征，可以根据brand，燃油类型，gearbox类型，车型等，都可以，这里只拿一个举例，其他的类似，可以封装成一个函数处理。
以gearbox构建统计特征：

train_data_gearbox = train_data.copy()   # 不要动
train_datatrain_data_gearbox['gearbox'] = cat_data['gearbox'][:train_data.shape[0]]
train_data_gearbox['price'] = train_target
train_gb = train_data_gearbox.groupby('gearbox')
all_info = {}
for kind, kind_data in train_gb:    info = {}    kind_data = kind_data[kind_data['price'] > 0]    info['gearbox_count'] = len(kind_data)    info['gearbox_price_max'] = kind_data.price.max()    info['gearbox_price_median'] = kind_data.price.median()    info['gearbox_price_min'] = kind_data.price.min()    info['gearbox_price_sum'] = kind_data.price.sum()    info['gearbox_std'] = kind_data.price.std()    info['gearbox_price_average'] = round(kind_data.price.sum() / (len(kind_data) + 1), 2)    all_info[kind] = info
gearbox_fe = pd.DataFrame(all_info).T.reset_index().rename(columns={"index": "gearbox"})
cat_data = cat_data.merge(gearbox_fe, how='left', on='gearbox')

当然下面就可以把bodyType和fuelType删除，因为该提取的信息也提取完了，该独热的独热。

# 删掉bodyType和fuelType，然后把gearbox， car_class is_fuel独热一下， 这个不能太早，构造晚了统计特征之后再独热
del cat_data['bodyType']
del cat_data['fuelType']
cat_data = pd.get_dummies(cat_data, columns=['gearbox', 'car_class', 'is_fuel', 'notRepairedDamage'])

数据特征的构造
数值特征这块，由于大部分都是匿名特征，处理起来不是太好处理，只能尝试一些加减组合和统计对里程进行一个分箱操作
一部车有效寿命30万公里，将其分为5段，每段6万公里，每段价值依序为新车价的5/15、4/15、
3/15、2/15、1/15。假设新车价12万元，已行驶7.5万公里（5年左右），那么该车估值为12万元
×（3+3+2+1）+15=7.2万元。

# 分成三段
bins = [0, 5, 10, 15]
num_data['kil_bin'] = pd.cut(num_data['kilometer'], bins, labels=False)

V系列特征的统计特征
平均值，总和和标准差

v_features = ['v_' + str(i) for i in range(15)]
num_data['v_sum'] = num_data[v_features].apply(lambda x: x.sum(), axis=1)
num_data['v_mean'] = num_data[v_features].apply(lambda x: x.mean(), axis=1)
num_data['v_std'] = num_data[v_features].apply(lambda 
x: x.std(), axis=1)

1.6 特征筛选

特征筛选就是在高维度、已量化的特征向量中选择对指定任务更有效的特征组合，进一步提升模型性能。
详细可见特征提升之特征提取、特征筛选