C++数据结构X篇_19_排序基本概念及冒泡排序（重点是核心代码，冒泡是稳定的排序）

文章目录

1. 排序基本概念
2. 冒泡排序
- 2.1 核心代码
- 2.2 冒泡排序代码
- 2.3 查看冒泡排序的时间消耗
- 2.4 冒泡排序改进版减小时间消耗

1. 排序基本概念

现实生活中排序很重要，例如:淘宝按条件搜索的结果展示等。

概念
排序是计算机内经常进行的一种操作，其目的是将一组“无序”的数据元素调整为“有序”的数据元素。
排序数学定义：
假设含 n 个数据元素的序列为( R1, R2，… Rn) 其相应的关键字序列为( K1, K2，., Kn)，这些关键字相互之间可以进行比较，即在它们之间存在着这样一个关系：Kp1≤Kp2≤…≤Kpn
按此固有关系将上式记录序列重新排列为(Rp1,Rp2，…，Rpn)的操作称作排序
排序的稳定性
如果在序列中有两个数据元素r[i]和r[j]，它们的关键字 k[i]==k[j]，且在排序之前，对象 r[i]排在r[j]前面。如果在排序之后，对象 r[i]仍在r[j]前面，则称这个排序方法是稳定的，否则称这个排序方法是不稳定的。
多关键字排序
排序时需要比较的关键字多余一个，排序结果首先按关键字 1 进行排序，当关键字1相同时按关键字 2 进行排序，当关键字 n-1 相同时按关键字n进行排序，对于多关键字排序，只需要在比较操作时同时考虑多个关键字即可 !
排序中的关键操作
- 比较：任意两个数据元素通过比较操作确定先后次序。
- 交换：数据元素之间需要交换才能得到预期结果
内排序和外排序
- 内排序：在排序过程中，待排序的所有记录全部都放置在内存中，排序分为：内排和外排序。
- 外排序：由于排序的记录个数太多，不能同时放置在内存，整个排序过程需要在内外存之间多次交换数据才能进行。
排序的审判
- 时间性能：关键性能差异体现在比较和交换的数量
- 辅助存储空间：为完成排序操作需要的额外的存储空间，必要时可以“空间换时间”
- 算法的实现复杂性：过于复杂的排序法会影响代码的可读性和可维护性，也可能影响排序的性能
总结
- 排序是数据元素从无序到有序的过程
- 排序具有稳定性，是选择排序算法的因素之一
- 比较和交换是排序的基本操作
- 多关键字排序与单关键字排序无本质区别
- 排序的时间性能是区分排序算法好坏的主要因素

2. 冒泡排序

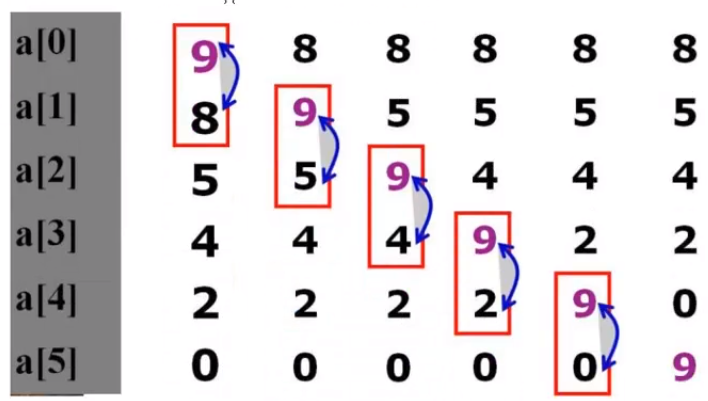
冒泡排序就是相邻两个元素进行交换，可以从上往下冒，也可以从下往上冒，下图为一个循环的冒泡。
在这里插入图片描述

2.1 核心代码

//冒泡排序
void bubble_sort(int arr[], int length)
{for (int i = 0; i < length - 1; i++){for (int j = 0; j < length - i - 1; j++){//此处为升序，降序的话arr[j] < arr[j + 1]if (arr[j] > arr[j + 1])  //升序{swap(&arr[j], &arr[j + 1]);}}}
}

2.2 冒泡排序代码

实现冒泡排序的代码如下

#include <iostream>
#include <time.h>
using namespace std;#define MAX 10void swap(int* a, int* b)
{int temp = *a;*a = *b;*b = temp;
}//打印数组
void printArr(int arr[])
{for (int i = 0; i < 10; i++){cout << arr[i] << endl;}
}//冒泡排序
void bubble_sort(int arr[], int length)
{for (int i = 0; i < length - 1; i++){for (int j = 0; j < length - i - 1; j++){if (arr[j] > arr[j + 1])  //升序{swap(&arr[j], &arr[j + 1]);}}}printArr(arr);
}int main()
{int arr[MAX];//生成随机数srand((unsigned int)time(NULL));for (int i=0;i<MAX;i++){arr[i] = rand() % MAX;}bubble_sort(arr, MAX);system("pause");return 0;
}

2.3 查看冒泡排序的时间消耗

敲代码查看冒泡排序的时间消耗

#include <iostream>
#include <time.h>
#include <sys/timeb.h>using namespace std;#define MAX 10000//获取系统当前时间,ms为单位
long getSystemTime()
{struct timeb tb;ftime(&tb);return tb.time * 1000 + tb.millitm;
}void swap(int* a, int* b)
{int temp = *a;*a = *b;*b = temp;
}//打印数组
void printArr(int arr[])
{for (int i = 0; i < 10; i++){cout << arr[i] << endl;}
}//冒泡排序
void bubble_sort(int arr[], int length)
{for (int i = 0; i < length - 1; i++){for (int j = 0; j < length - i - 1; j++){if (arr[j] > arr[j + 1])  //升序{swap(&arr[j], &arr[j + 1]);}}}//printArr(arr);
}int main()
{int arr[MAX];//生成随机数srand((unsigned int)time(NULL));for (int i=0;i<MAX;i++){arr[i] = rand() % MAX;}long tStart = getSystemTime();bubble_sort(arr, MAX);long tEnd = getSystemTime();cout << tEnd - tStart << endl;system("pause");return 0;
}

运行结果：3247ms
在这里插入图片描述

2.4 冒泡排序改进版减小时间消耗

下图中，当9排到第一个就已经是有序的了。之前的版本每一个都需要进行比较，我们可以判断其在有序的情况下就可以退出了，没有必要一直比较循环。这样就提高了冒泡排序的效率。
在这里插入图片描述
在核心代码中有一次循环并不执行swap(&arr[j], &arr[j + 1]);就代表已经有序了

int flag=0;//标识没有排序好
//冒泡排序
void bubble_sort(int arr[], int length)
{for (int i = 0; i < length - 1 && flag==0; i++){for (int j = 0; j < length - i - 1; j++){flag = 1;//认为已经排序好//此处为升序，降序的话arr[j] < arr[j + 1]if (arr[j] > arr[j + 1])  //升序{flag=0;swap(&arr[j], &arr[j + 1]);}}}
}

整体代码为：

#include <iostream>
#include <time.h>
#include <sys/timeb.h>using namespace std;#define MAX 10000//获取系统当前时间,ms为单位
long getSystemTime()
{struct timeb tb;ftime(&tb);return tb.time * 1000 + tb.millitm;
}void swap(int* a, int* b)
{int temp = *a;*a = *b;*b = temp;
}//打印数组
void printArr(int arr[])
{for (int i = 0; i < 10; i++){cout << arr[i] << endl;}
}int flag = 0;//标识没有排序好
//冒泡排序
void bubble_sort(int arr[], int length)
{for (int i = 0; i < length - 1 && flag == 0; i++){for (int j = 0; j < length - i - 1; j++){flag = 1;//认为已经排序好//此处为升序，降序的话arr[j] < arr[j + 1]if (arr[j] > arr[j + 1])  //升序{flag = 0;swap(&arr[j], &arr[j + 1]);}}}
}int main()
{int arr[MAX];//生成随机数srand((unsigned int)time(NULL));for (int i=0;i<MAX;i++){arr[i] = rand() % MAX;}long tStart = getSystemTime();bubble_sort(arr, MAX);long tEnd = getSystemTime();cout << tEnd - tStart << endl;system("pause");return 0;
}