Codeforces Round 905 (Div. 3)

A. Morning

题意

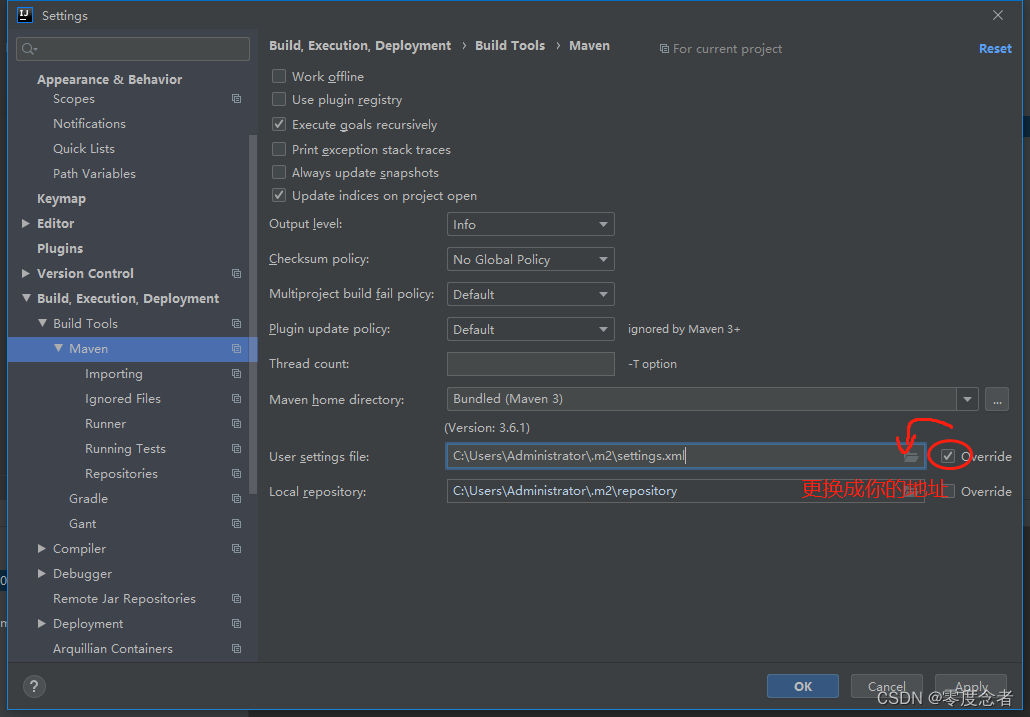
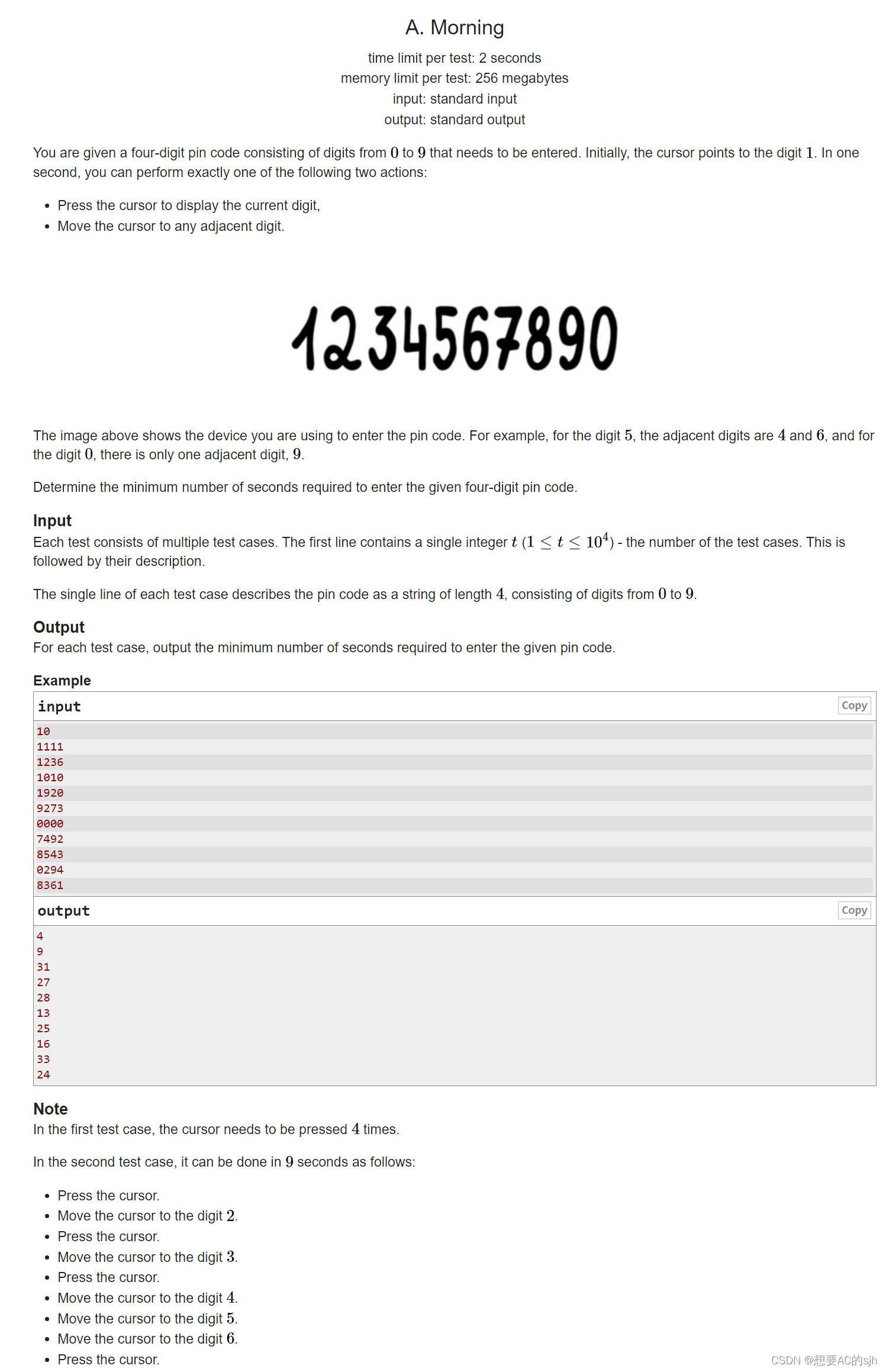
从一开始，每一次操作可以选择当前的数字打印或者是移动到左右相邻的数字，具体排列看上图，给出一个标签四位数，求打印出来的操作次数

思路

求相邻两个数字之间的距离差累加

核心代码

void solve()
{string s;cin>>s;int ans=0;if(s[0]=='0')s[0]+=10;ans=abs(s[0]-'1');for(int i=1;i<4;++i){if(s[i]=='0')s[i]+=10;ans+=abs(s[i]-s[i-1]);}ans+=4;cout<<ans<<endl;
}

B. Chemistry

题意

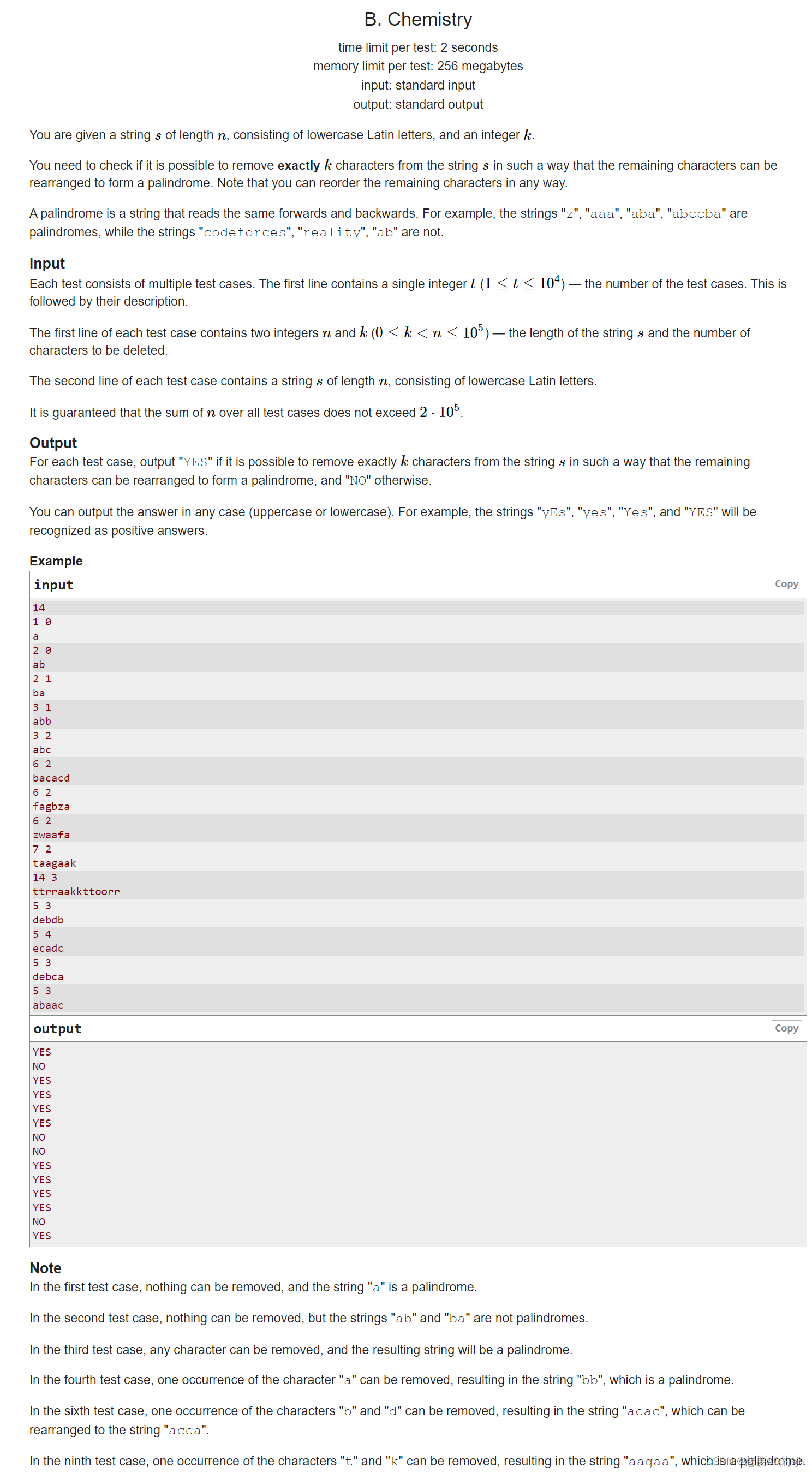
给你一个长度为n的字符串以及可以删除的字符个数k，询问删除之后重新排列能否构成回文字符串

思路

要想构成回文字符串所有的字母出现的次数都要是偶数，除了最中间的那一个字母可以是出现奇数次。然后是删除的k次，如果k大于原字符串中出现奇数次数的字母个数，那么后面多余的次数就可以去删除出现偶数次的字母，最后一定能够构成回文字符串，k不够大的话那就不能构成了

核心代码

void solve()
{int n,k;scanf("%d%d",&n,&k);string s;cin>>s;int len=s.size();int arr[26]{};for(int i=0;i<len;++i){arr[s[i]-'a']++;}int geshu=0;int sum=0;for(int i=0;i<26;++i){if(arr[i]&1)geshu++;sum+=arr[i];}if(geshu<=k+1)printf("YES\n");else printf("NO\n");
}

C. Raspberries

题意

给你一组长度为n的数组，以及一个整数k，每一次可以对数组里面的任意一个数字进行加一操作，问最少执行多少次可以使得这个数组里面所有的数字的乘积是k的倍数

思路

如果k是质数，那么我们只需要满足这个数组里面有一个数字是k的倍数就可以了，可以对每一个数字进行枚举找最小的那一个，但是如果是合数怎么操作呢，本题只有一个合数4，单独进行特判就可以了

核心代码

void solve()
{int n,k;scanf("%d%d",&n,&k);int minzhi=INT_MAX;int input;int oushu=0;int jishu=0;for(int i=0;i<n;++i){scanf("%d",&input);if(input&1)jishu++;else oushu++;if(input%k==0)minzhi=0;else minzhi=min(minzhi,k-input%k);}if(k!=4){printf("%d\n",minzhi);return ;}if(oushu>=2)printf("0\n");else if(oushu==1&&jishu>=1)printf("%d\n",min(minzhi,1));else if(oushu==1&&jishu==0)printf("%d\n",min(minzhi,2));else if(oushu==0&&jishu>=2)printf("%d\n",min(minzhi,2));return ;
}

D. In Love

题意

每一次增加一个边或者减少一个边，操作完之后询问是否存在一对不重合的边

思路

如果存在一对不重合的边，那么必然存在一条边的右端点小于一条边的左端点，我们只需要看最小的右端点是否小于最大的左端点即可

核心代码

void solve()
{int n;cin>>n;multiset<int>l,r;for(int i=0;i<n;++i){char a;int x,y;cin>>a>>x>>y;if(a=='+'){l.insert(x);r.insert(y);}else{l.erase(l.find(x));r.erase(r.find(y));}if(l.size() > 1 && *r.begin() < *l.rbegin())printf("YES\n");else printf("NO\n");}
}

E. Look Back

题意

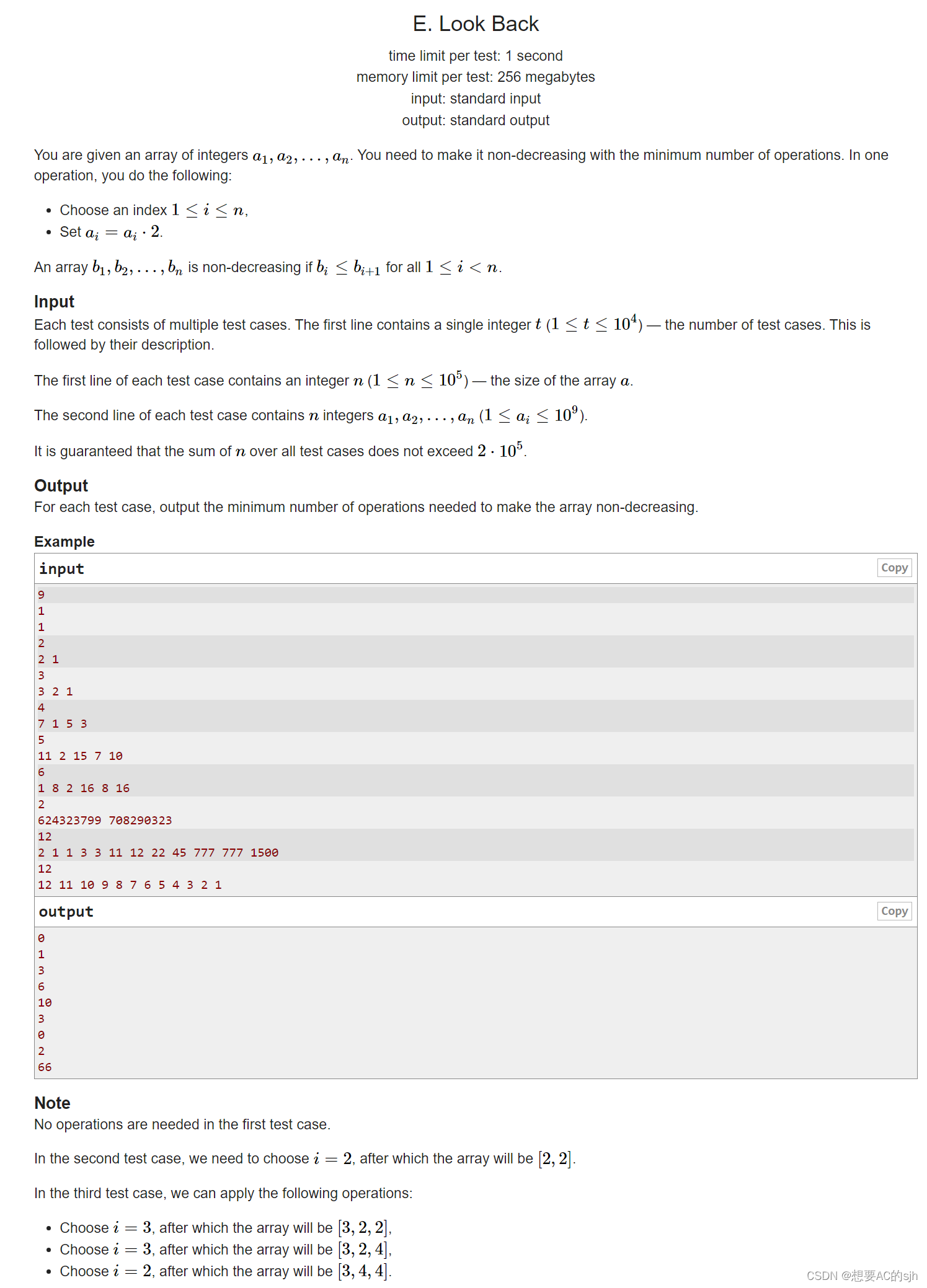
给你一组长度为n的数组，每一次可以选择一个数组乘以2，最少需要多少次可以使得这个数组变成一个非递减数组

思路

只需要从前往后进行贪心枚举就可以了，但是这个题目数据量有点大，不能直接存储每一个数字变化之后的数字，需要转化一下，比如我们可以通过前后两个数字的大小倍数关系来求

核心代码

void solve()
{int n;scanf("%d",&n);long long a=0,b;long long ans=0;long long num=0;long long bei=0;scanf("%lld",&a);for(int i=1;i<n;++i){scanf("%lld",&b);if(b>a){int a2=a;while(a2<=b&&a2!=0){a2<<=1;num--;}num++;num=num>0?num:0;ans+=num;a=b;continue;}else if(a==b){ans+=num;continue;}else{int b2=b;while(b2<a){num++;b2<<=1;}ans+=num;a=b;}}printf("%lld\n",ans);
}