LeetCode T435 无重叠区间
题目链接:435. 无重叠区间 - 力扣(LeetCode)

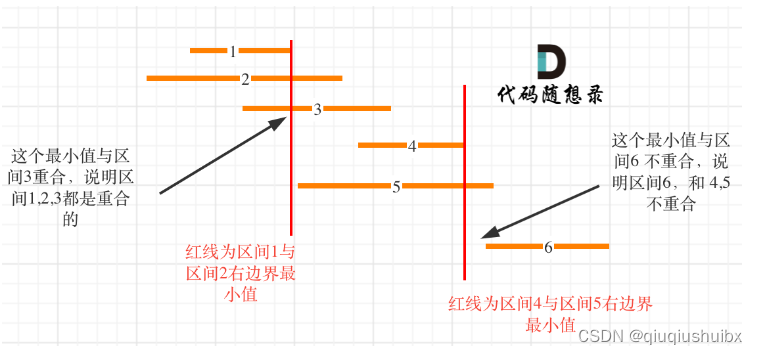
题目思路:
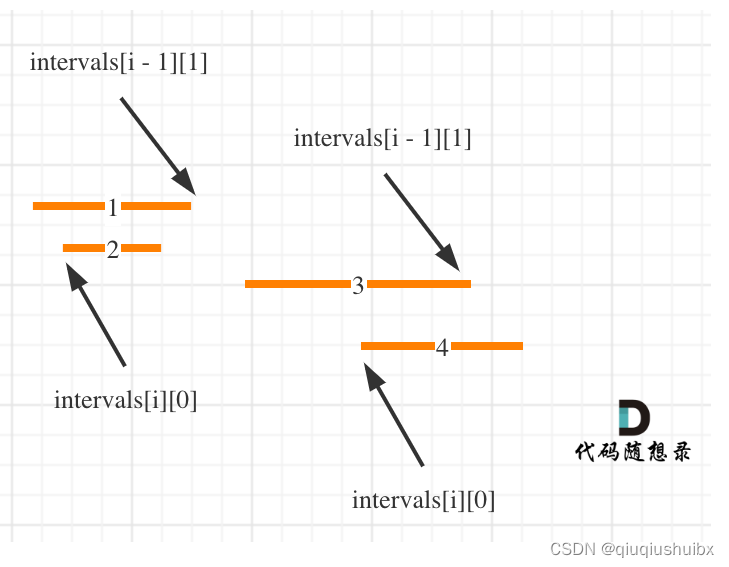
这题思路和昨天的打气球类似,我们需要按照左区间或者右区间进行排序,然后哦判断第i个区间的左端点和第i-1个区间的右端点的大小关系,,如果大于等于,那么就无需操作,一旦小于了,那么就发生了重叠,相应的我们更新左端点为两者之间的较小值,并且要对定义的count进行++,这样就统计了重叠的个数,也就是我们要删除的个数.总体思路类似于昨天
题目代码:
class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals, (a,b)-> {return Integer.compare(a[0],b[0]);});int count = 0;for(int i = 1;i < intervals.length;i++){if(intervals[i][0] < intervals[i-1][1]){intervals[i][1] = Math.min(intervals[i - 1][1], intervals[i][1]);count++;}}return count;}
}
LeetCode T763 划分字母区间
题目链接:763. 划分字母区间 - 力扣(LeetCode)

题目思路:
首先我们明确题意,这题的要求是对字符串中的第一个字母开始,再找到第一个字母的过程,途中遇见的字母必须全部包含在内,最后分割后的字符串,每个字母都只出现在这个子串中,有人不理解这道题的题目
这里举个例子
开头是a,这里我们就要找到下一个a,但是找寻的途中遇见了b,这里所有的b也必须包含在内了,以此类推.我们的思路是对每个字母进行映射,每次更新字母最后出现的位置,然后遍历数组,看到达那个位置的途中有没有遇见更大的位置,有则更新,当我遍历的位置等于我目前的最大位置时,将目前为止减去开始位置的大小加入到结果数组中.
题目代码:
class Solution {public List<Integer> partitionLabels(String s) {List<Integer> result = new ArrayList<>();int[] edge = new int[26];char[] chars = s.toCharArray();for(int i = 0;i<chars.length;i++){edge[chars[i] - 'a'] = i;}int index = 0;int lastedge = -1;for(int i = 0;i<chars.length;i++){index = Math.max(edge[chars[i] - 'a'],index);if(index == i){result.add(i-lastedge);lastedge = i;}}return result;}
}LeetCode T56 合并区间
题目链接:56. 合并区间 - 力扣(LeetCode)

题目思路:
我们这里使用和之前一样的策略来解决问题,这里首先按照左区间进行排序一次,我们进行一次for循环,定义一个start来标记区间的起始位置,一个bound来标记结束位置,我们尽心判断,如果区间的左区间大于上一个的右区间,这里就没有重复的,我们就进行添加,添加完更新左右区间,否则就直接更新右区间为原来bound和现在的最大值,以包含覆盖这一整个区间,最后结束之后再添加最后一个区间,因为这里比较了少了一次,所以要额外加一个元素.最后以二维数组形式返回即可.
题目代码:
class Solution {public int[][] merge(int[][] intervals) {List<int[]> result = new ArrayList<>();Arrays.sort(intervals,(a,b)->{return a[0] - b[0]; });int start = intervals[0][0];int bound = intervals[0][1];for(int i = 0;i<intervals.length;i++){if(intervals[i][0]>bound){result.add(new int[]{start,bound});start = intervals[i][0];bound = intervals[i][1];}else{bound = Math.max(bound,intervals[i][1]);}}result.add(new int[]{start,bound});return result.toArray(new int[result.size()][]);}
}