带IV的分组加密下密文分散存储且存在混淆密文片段的多项式时间解密方案

在使用带IV的分组加密模式下，考虑这样一个场景：分组加密后，每组密文都被分散保存，且在恢复的时候，每组密文会和n个混淆的密文一起提供，此时，若想完整的恢复明文，需要一个多项式时间的方案来剔除所有混淆密文。本文提出了一种基于可密文前缀的方案，能够在多项式的时间内完成解密。
PS：文章的名字也太难取了，赶时间随便取了个。

文章目录

1.背景
2.Idea
3.真实场景的问题
4.应用场景

1.背景

使用非 $ECB$ 模式的分组加密（假设为 $CBC$ ），假设为加密算法为 $A ES$ ，初始向量为 $I V$ ，密钥为 $k$ ，明文为 $\mathcal M$ ，共分为了 $n$ 个组进行加密，加密后的密文为 $\mathcal C$ 。

我们把密文分为 $n$ 个组，每组密文为 $c_{1},c_{2}...,c_{n}$ ，这 $n$ 组密文按顺序分散存储，且每组密文存在 $t$ 个混淆密文 $c_{i_1},c_{i_2}...,c_{i_{t}}$ 。

现在，按顺序的拿出所有密文分组（包含混淆密文分组），要恢复完整的明文 $\mathcal M$ 。

2.Idea

所有分组的存储和给出都是按顺序进行的，所以难点在如何把 $t$ 个混淆密文去除。

想法：
1.对于第一个分组，可以很快速的确认出真实的密文片段 $c_{1}$ ，只需要将 $c_{1_1},c_{1_2}...,c_{1_{t}}$ 依次放入解密中尝试解密即可 $Dec(c_{1_i}, k), i\in[1,t+1]$ ，由于 $I V$ 是确定的，所以只有真实的 $c_{1}$ 能够成功解密。

2.在确定了 $c_{1}$ 后，继续尝试 $Dec(c_{1} + c_{j_i}, k), i\in[1,t+1],j\in[2,n]$ ，从而可以确认 $c_{j}$ 。

这样，通过一步步确认真实密文前缀的方式，能够区分开所有混淆密文，而且是在多项式的时间内。当然，前提条件是解密机能够准确判断是否解密成功。

3.真实场景的问题

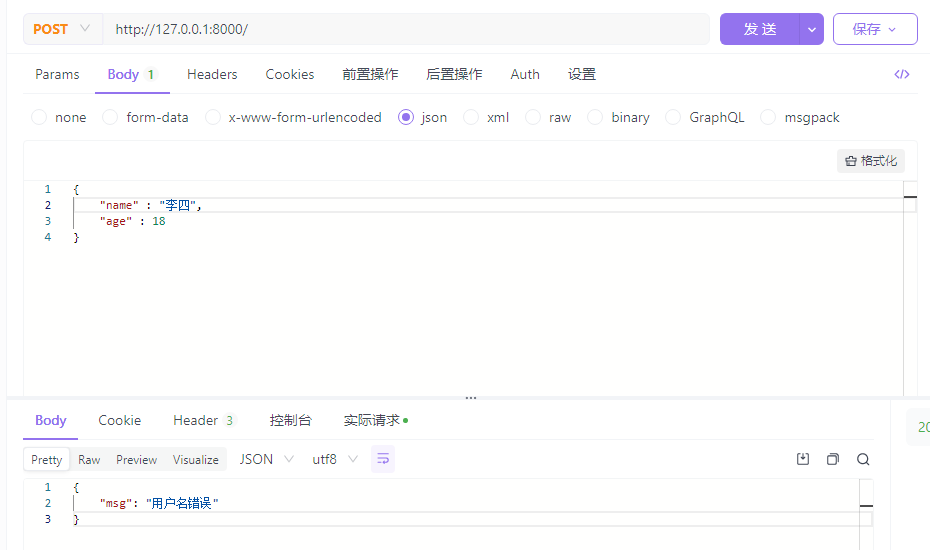
在用JavaScript实现上述方案的时候，存在一个问题：如何判断解密机是否成功解密。

常见的思路是：加密之前会先对字符进行编码，密文解密后会进行解码，如果解码成功就意味着解密成功，解码出现异常就是解密失败。

这种思路在上文背景下，会有部分场景失效，考虑如下场景：一段中文字符经由UTF-8编码后，每个中文字符通常会占2-3个字节，假设分组的长度是32字节，那么一个密文分组解密后，很有可能会因为尾部存在一个不完整编码的中文字符而解码失败，导致解密机判断为解密失败。

解决上述问题的一个办法是，找一个能把需要使用到的各种字符都编码成不会被分组长度隔断的编码，例如，如果只存在中文，那么使用GB2312就可以完美解决这个问题，因为每个汉字占两个字节，不可能出现某个分组的尾部包含不完整编码的汉字。

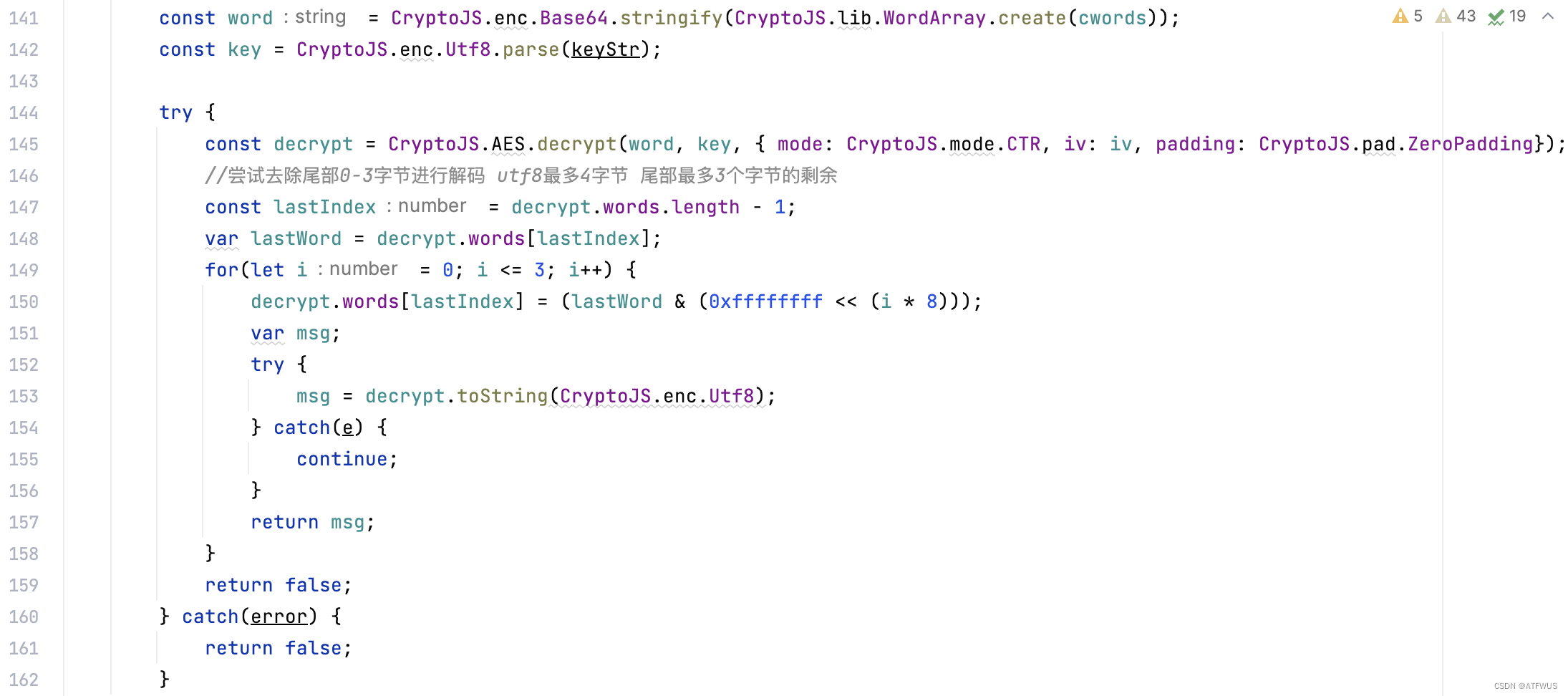
但是这样的办法拓展性不强，如果需要用到各种各样字符的话，找一个合适的编码比较麻烦。于是有另一个思路：尝试去除（置0字节）解密后密文尾部的0-2个字节，即可完美的解决这个问题。例如，如果使用UTF-8编码汉字，某个分组尾部容易存在1-2不完整编码的字节，那么我们尝试去除尾部的0-2个字节，就可以保证所有情况都完整的考虑了。

使用其它的编码也类似，主要考虑某个分组尾部可能残留多少个不完整编码的字节。下面是一个JS实现的核心代码示例。

在这里插入图片描述