从零开始实现神经网络(一)

参考文章：神经网络介绍

一、神经元

这一神经网络的基本单元，神经元接受输入，对它们进行一些数学运算，并产生一个输出。

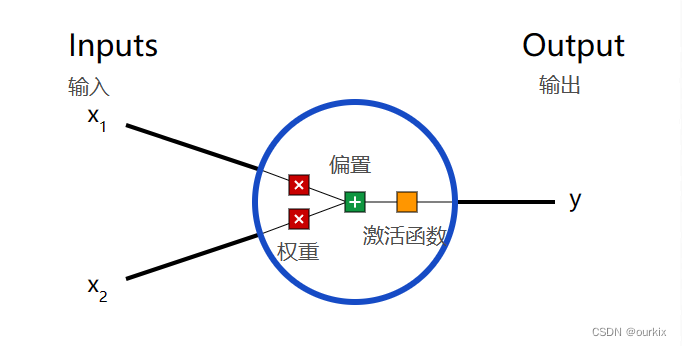
这里有三步。

首先，将每个输入（X1）乘以一个权重：

$x_1 * w_1$

$x_2 * w_2$

接下来，将所有加权输入与偏置相加:

$( x_1 * w _1 ) + ( x_2 * w_2 ) + b$

最后，总和通过激活函数传递：

$y = f(w_1*x_1 + w_2 * x_2 + b)$

激活函数

激活函数用于将无界输入转换为具有良好、可预测形式的输出。常用的激活函数是sigmoid功能：

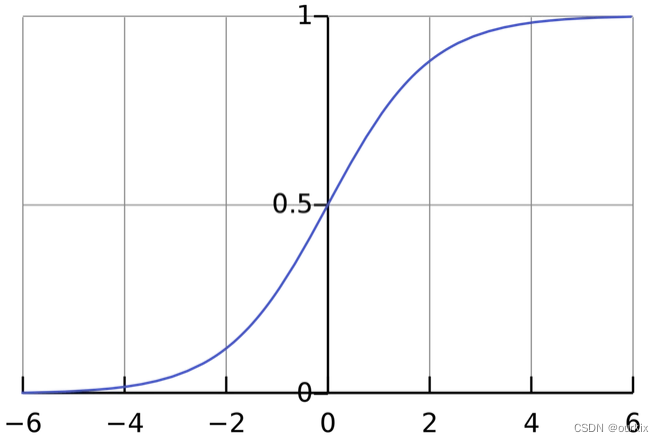
你可以把它想象成,压缩零到负无穷的数字到[-1,0],压缩0到正无穷的数字到[0,1]

举个例子：

这里写成向量形式，假设权重W = {w1,w2} = {0,1},输入X = {x1,x2} = {2,3},偏置b为1。

那么有一下计算：

$(X\cdot W ) + b = ( x_1 * w _1 ) + ( x_2 * w_2 ) + b$

$= 0 * 2 +1*3 +4$

$=7$

$y = f(w_1*x_1 + w_2 * x_2 + b) = f(7) = 0.9999$

下面来实现下代码：

import numpy as npdef sigmoid(x):# Our activation function: f(x) = 1 / (1 + e^(-x))return 1 / (1 + np.exp(-x))class Neuron:def __init__(self, weights, bias):self.weights = weightsself.bias = biasdef feedforward(self, inputs):# Weight inputs, add bias, then use the activation functiontotal = np.dot(self.weights, inputs) + self.biasreturn sigmoid(total)weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4                   # b = 4
n = Neuron(weights, bias)x = np.array([2, 3])       # x1 = 2, x2 = 3
print(n.feedforward(x))    # 0.9990889488055994

二. 将神经元组合成神经网络

神经网络只不过是一堆连接在一起的神经元。下面是一个简单的神经网络的样子：

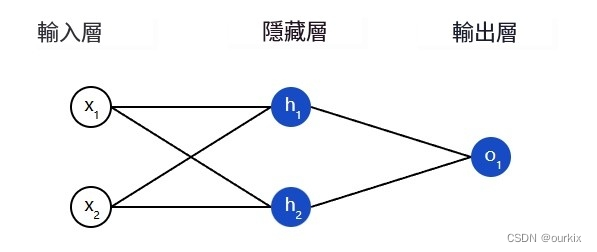
该网络有 2 个输入（x1和x2），一个带有 2 个神经元的隐藏层（ℎ1和ℎ2），以及具有 1 个神经元（o1).请注意，输入o1是来自ℎ1和h2- 这就是使它成为一个网络的原因。

隐藏层是输入（第一层）和输出（最后一层）之间的任何层。可以有多个隐藏层！

示例：前馈

让我们使用上图的网络，并假设所有神经元具有相同的权重w=[0,1]，相同的偏差b=0，以及相同的 S 形激活函数。让h1,h2,o1表示它们所代表的神经元的输出。

如果我们传入输入会发生什么x=[2,3]?

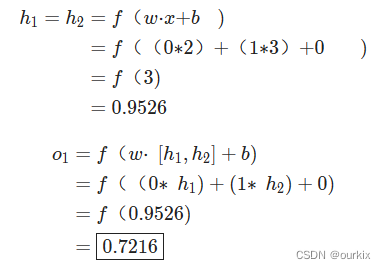
用于输入的神经网络的输出x=[2,3]是0.7216很简单，对吧？

神经网络可以有任意数量的层，这些层中可以有任意数量的神经元。基本思想保持不变：通过网络中的神经元向前馈送输入，以在最后获得输出。为简单起见，在本文的其余部分，我们将继续使用上图的网络。

神经网络的代码实现：

import numpy as np# ... code from previous section hereclass OurNeuralNetwork:'''A neural network with:- 2 inputs- a hidden layer with 2 neurons (h1, h2)- an output layer with 1 neuron (o1)Each neuron has the same weights and bias:- w = [0, 1]- b = 0'''def __init__(self):weights = np.array([0, 1])bias = 0# The Neuron class here is from the previous sectionself.h1 = Neuron(weights, bias)self.h2 = Neuron(weights, bias)self.o1 = Neuron(weights, bias)def feedforward(self, x):out_h1 = self.h1.feedforward(x)out_h2 = self.h2.feedforward(x)# The inputs for o1 are the outputs from h1 and h2out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))return out_o1network = OurNeuralNetwork()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421

三. 训练神经网络，第 1 部分

假设我们有以下测量值：

名字	重量（磅）	高度（英寸）	性
爱丽丝	133	65	F
鲍勃	160	72	M
查理	152	70	M
黛安娜	120	60	F

让我们训练我们的网络，根据某人的体重和身高预测他们的性别：

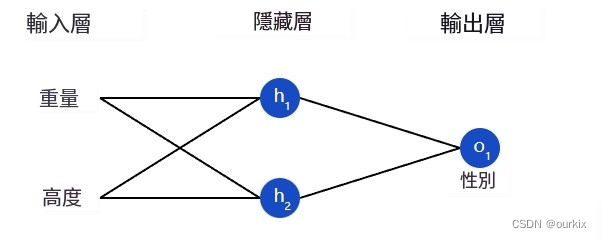
我们将用0代表男性，1代表女性，我们还将处理数据以使其更易于使用：

名字	重量（减去 135）	高度（减去 66）	性
爱丽丝	-2	-1	1
鲍勃	25	6	0
查理	17	4	0
黛安娜	-15	-6	1

我随意选择了减去的数值（135和66）以使数值看起来更好。通常，会按平均值移动。

损失

在我们训练网络之前，我们首先需要一种方法来量化它做得有多“好”，以便它可以尝试做得“更好”。这就是损失所在。

我们将使用均方误差 （MSE）损失：

$MSE = \frac{1}{n}\sum^n_{i=1} (yTrue - yPred)^2$

让我们分解一下：

n是样本数，即4（爱丽丝，鲍勃，查理，戴安娜）。
y表示要预测的变量，即性别。
yTrue是变量的真实值（“正确答案”）。例如yTRue因为爱丽丝的性别为1（女）。
yPred是变量的预测值。这是我们的网络输出的任何内容。

$(yTrue - yPred)^2$ 称为平方误差。我们的损失函数只是取所有平方误差的平均值（因此得名均方误差）。我们的预测越好，我们的损失就越低！

更好的预测=更低的损失。

训练网络=试图将其损失降至最低。

损失计算示例

假设我们的网络总是输出0换句话说，它相信所有人类都是男性🤔。我们的损失会是什么？

名字	yTRue	$(yTrue - yPred)^2$
爱丽丝	1	1
鲍勃	0	0
查理	0	0
黛安娜	1	1

$MSE=\frac{1}{4}(1+0+0+1) = 0.5$

均方误差的代码实现：

import numpy as npdef mse_loss(y_true, y_pred):# y_true and y_pred are numpy arrays of the same length.return ((y_true - y_pred) ** 2).mean()y_true = np.array([1, 0, 0, 1])
y_pred = np.array([0, 0, 0, 0])print(mse_loss(y_true, y_pred)) # 0.5

四. 训练神经网络，第 2 部分

反向传播

我们现在有一个明确的目标：尽量减少神经网络的损失。我们知道我们可以改变网络的权重和偏差来影响其预测，但是我们如何以减少损失的方式做到这一点呢？

为简单起见，让我们假设我们的数据集中只有爱丽丝：

名字	重量（减去 135）	高度（减去66）	性
爱丽丝	-2	-1	1

那么只是爱丽丝的均方误差损失(最后会带入yTrue的值进去)：

$MSE = \frac{1}{1}\sum^1_{i=1} (yTrue - yPred)^2$

$=(yTrue - yPred)^2$

$=(1 - yPred)^2$

另一种考虑损失的方法是作为权重和偏差的函数。让我们标记网络中的每个权重和偏差：

然后，我们可以将损失写为多变量函数：

L(w1,w2,w3,w4,w5,w6,b1,b2,b3)

想象一下，我们想调整w1.损失将如何L如果我们改变了，就改变w1?

这是一个偏导数的问题 $\frac{\partial L}{\partial w_1}$ 可以回答。我们如何计算它？

首先，让我们根据以下方法(链式法则)重写偏导数：

$\frac{\partial L}{\partial w_1} =\frac{\partial L}{\partial yPred} * \frac{\partial yPred}{\partial w_1}$

这里 $\frac{\partial L}{\partial yPred}$ 我们可以求得，由于前面的MSE均方误差计算的就是神经网络的误差，MSE作为损失函数，所以有等式：

$L(w1,w2,w3,w4,w5,w6,b1,b2,b3) = (1 - yPred)^2$

所以可以得出：

$\frac{\partial L}{\partial yPred} = \frac{\partial (1 - yPred)^2}{\partial yPred}$

这里使用符合函数求导法则(对于 $f(g(x))$ 函数的x进行求导，将得到 $= f(g(x))^{'}*g(x)^{'}$ )：

$= 2*(1-yPred)*(1-yPred)^{'}$

$=2*(1-yPred)*(-1)$

$=-2*(1-yPred)$

然后我们再搞清楚 $\frac{\partial yPred}{\partial w_1}$ ，由于yPred是预测值，而预测值由激活函数输出，所以能够得到等式：

$yPred = o_1 = f(w_5*h_1 + w_6 * h_2 + b_3)$

由于改变w1只对h1有影响，所以可以写成：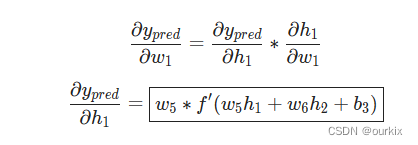

我们再对h1做同样的步骤（h1是上一层的激活函数）, $\frac{\partial h_1}{\partial w_1}$ ，同样是复合函数求导法则：

对于激活函数sigmoid的倒数：

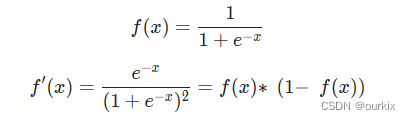
最终整合起来：

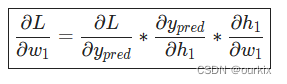
这种通过逆向计算偏导数的系统称为反向传播。

推导当前神经网络反向传播所用到的所有偏导公式：

$\frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial yPred} * \frac{\partial yPred}{\partial h_1} * \frac{\partial h_1}{\partial w_1}$

$\frac{\partial L}{\partial w_2} = \frac{\partial L}{\partial yPred} * \frac{\partial yPred}{\partial h_1} * \frac{\partial h_1}{\partial w_2}$

$\frac{\partial L}{\partial w_3} = \frac{\partial L}{\partial yPred} * \frac{\partial yPred}{\partial h_2} * \frac{\partial h_2}{\partial w_3}$

$\frac{\partial L}{\partial w_4} = \frac{\partial L}{\partial yPred} * \frac{\partial yPred}{\partial h_2} * \frac{\partial h_2}{\partial w_4}$

$\frac{\partial L}{\partial w_5} = \frac{\partial L}{\partial yPred} * \frac{\partial yPred}{\partial w_5}$

$\frac{\partial L}{\partial w_6} = \frac{\partial L}{\partial yPred} * \frac{\partial yPred}{\partial w_6}$

$\frac{\partial L}{\partial b_1} = \frac{\partial L}{\partial yPred} * \frac{\partial yPred}{\partial h_1} * \frac{\partial h_1}{\partial b_1}$

$\frac{\partial L}{\partial b_2} = \frac{\partial L}{\partial yPred} * \frac{\partial yPred}{\partial h_2} * \frac{\partial h_2}{\partial b_2}$

$\frac{\partial L}{\partial b_3} = \frac{\partial L}{\partial yPred} * \frac{\partial yPred}{\partial b_3}$

例子：

我们将继续假设数据集中只有爱丽丝：

名字	重量（减去 135）	高度（减去 66）	性
爱丽丝	-2	-1	1

让我们将所有权重初始化为1以及所有偏置为0.如果我们通过网络进行前馈传递，我们会得到：

网络输出yPred=0.524，这并不强烈支持男性或女性 .让我们计算一下 $\frac{\partial L}{\partial w_1}$

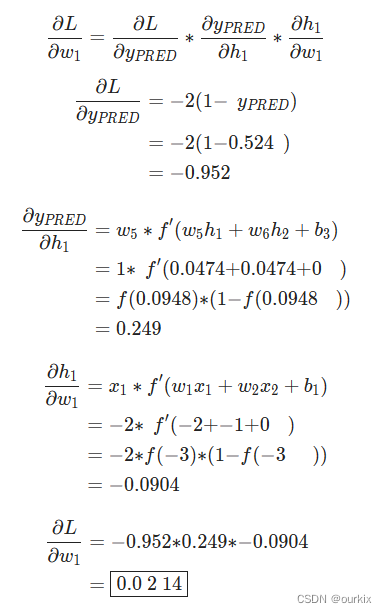
这里用到了上面所求得的sigmoid的倒数。

我们成功了！这告诉我们，由于 $\frac{\partial L}{\partial w_1}$ 所求的偏导结果为0.0214，是个正数，函数单调递增，所以

如果我们要增加w1(权重),L(损失)结果会增大一点点。

训练：随机梯度下降

我们现在拥有训练神经网络所需的所有工具！我们将使用一种称为随机梯度下降（SGD）的优化算法，该算法告诉我们如何改变权重和偏差以最小化损失。

就是这个方程式：

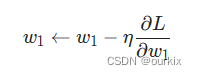
η是一个称为学习率的常数，它控制着我们训练的速度。我们所做的只是用旧权重减去学习率*偏导值:

如果 $\frac{\partial L}{\partial w_1}$ 的值为正数，w1的减少，会使得L减少。
如果 $\frac{\partial L}{\partial w_1}$ 的值为负数，w1的增加，会使得L减少。

如果我们对网络中的每个权重和偏差都这样做，损失将慢慢减少，我们的网络将得到改善。

我们的训练过程将如下所示：

从我们的数据集中选择一个样本。这就是它随机梯度下降的原因——我们一次只对一个样本进行操作。
计算所有损失相对于权重或偏差的偏导数（例如 $\frac{\partial L}{\partial w_1}$ ， $\frac{\partial L}{\partial w_2}$ 等）。
使用更新公式更新每个权重和偏差。
返回步骤 1。

让我们看看它的实际效果吧！

代码：一个完整的神经网络

终于到了实现一个完整的神经网络的时候了：

名字	重量（减去 135）	高度（减去 66）	性
爱丽丝	-2	-1	1
鲍勃	25	6	0
查理	17	4	0
黛安娜	-15	-6	1

import numpy as npdef sigmoid(x):# Sigmoid activation function: f(x) = 1 / (1 + e^(-x))return 1 / (1 + np.exp(-x))def deriv_sigmoid(x):# Derivative of sigmoid: f'(x) = f(x) * (1 - f(x))fx = sigmoid(x)return fx * (1 - fx)def mse_loss(y_true, y_pred):# y_true and y_pred are numpy arrays of the same length.return ((y_true - y_pred) ** 2).mean()class OurNeuralNetwork:'''A neural network with:- 2 inputs- a hidden layer with 2 neurons (h1, h2)- an output layer with 1 neuron (o1)*** DISCLAIMER ***:The code below is intended to be simple and educational, NOT optimal.Real neural net code looks nothing like this. DO NOT use this code.Instead, read/run it to understand how this specific network works.'''def __init__(self):# Weightsself.w1 = np.random.normal()self.w2 = np.random.normal()self.w3 = np.random.normal()self.w4 = np.random.normal()self.w5 = np.random.normal()self.w6 = np.random.normal()# Biasesself.b1 = np.random.normal()self.b2 = np.random.normal()self.b3 = np.random.normal()def feedforward(self, x):# x is a numpy array with 2 elements.h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)return o1def train(self, data, all_y_trues):'''- data is a (n x 2) numpy array, n = # of samples in the dataset.- all_y_trues is a numpy array with n elements.Elements in all_y_trues correspond to those in data.'''learn_rate = 0.1epochs = 1000 # number of times to loop through the entire datasetfor epoch in range(epochs):for x, y_true in zip(data, all_y_trues):# --- Do a feedforward (we'll need these values later)sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1h1 = sigmoid(sum_h1)sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2h2 = sigmoid(sum_h2)sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3o1 = sigmoid(sum_o1)y_pred = o1# --- Calculate partial derivatives.# --- Naming: d_L_d_w1 represents "partial L / partial w1"d_L_d_ypred = -2 * (y_true - y_pred)# Neuron o1d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)d_ypred_d_b3 = deriv_sigmoid(sum_o1)d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)# Neuron h1d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)d_h1_d_b1 = deriv_sigmoid(sum_h1)# Neuron h2d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)d_h2_d_b2 = deriv_sigmoid(sum_h2)# --- Update weights and biases# Neuron h1self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1# Neuron h2self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2# Neuron o1self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3# --- Calculate total loss at the end of each epochif epoch % 10 == 0:y_preds = np.apply_along_axis(self.feedforward, 1, data)loss = mse_loss(all_y_trues, y_preds)print("Epoch %d loss: %.3f" % (epoch, loss))# Define dataset
data = np.array([[-2, -1],  # Alice[25, 6],   # Bob[17, 4],   # Charlie[-15, -6], # Diana
])
all_y_trues = np.array([1, # Alice0, # Bob0, # Charlie1, # Diana
])# Train our neural network!
network = OurNeuralNetwork()
network.train(data, all_y_trues)

随着网络学习，我们的损失稳步减少：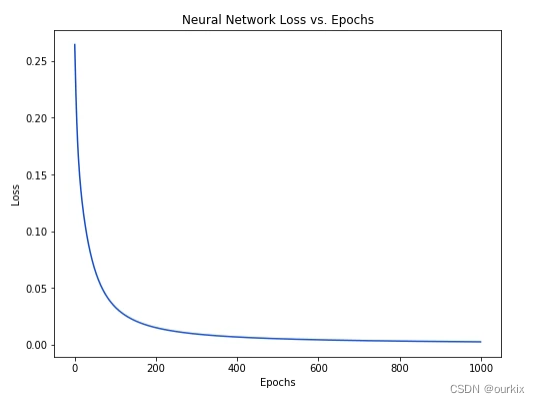

我们现在可以使用网络来预测性别：

# Make some predictions
emily = np.array([-7, -3]) # 128 pounds, 63 inches
frank = np.array([20, 2])  # 155 pounds, 68 inches
print("Emily: %.3f" % network.feedforward(emily)) # 0.951 - F
print("Frank: %.3f" % network.feedforward(frank)) # 0.039 - M