数据结构和算法解决的是执更快和更省资源的问题，快和省通过复杂度来衡量。

为什么需要复杂度分析？

代码跑一遍存在的问题：

1. 结果依赖环境。
2. 结果受数据结构和规模的影响很大，无法覆盖所有数据场景。

需要使用复杂度分析进行粗略的估计。

什么是 O 复杂度表示法？

以C++为例子，按照语句生成机器语言指令，我们假设每个机器指令执行时间相同为 unit_time，为了方便对每个语句进行分析，将代码写成如下格式：

int func(int n) 
{int sum = 0;        //1 * unit_time  for (int i = 1;     //1 * unit_timei <= n;         //n *  unit_time++i)            //n *  unit_time{sum = sum + i;  //n *  unit_time}return sum;//1 * unit_time
}

执行总时间为：(3n + 3 ) unit_time

下面代码进行分析：

int func(int n) 
{int sum = 0;    //1 * unit_time  for (int i = 1; //1 * unit_time  i <= n;     //n *  unit_time++i)        //n *  unit_time{for (int j = 1; //n *  unit_timej <= n;     //n^2 *  unit_time++j)        //n^2 *  unit_time{sum = sum + i * j;//n^2 *  unit_time}}return sum;//1 * unit_time
}

执行总时间为：(2 * n^2 + 3n + 3) * unit_time

结论：所有代码的执行时间 T(n)与语句执行次数f(n)成正比。

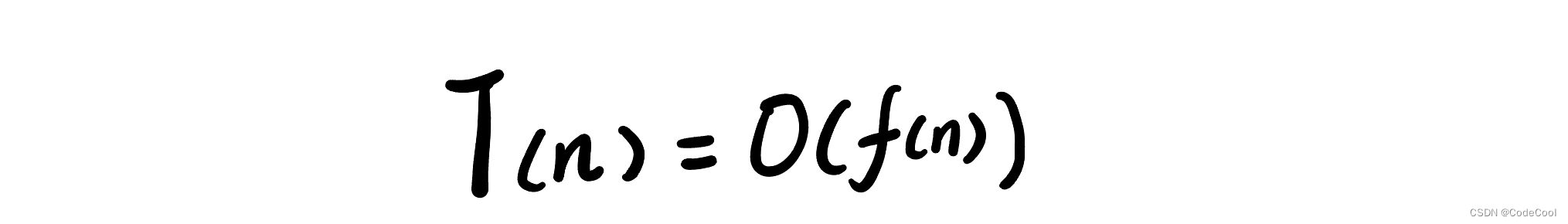
T(n)：代码执行时间。
f(n)：每个语句的执行次数总和。
n：数据规模。

大O表示：代码执行时间随数据规模增长的变化趋势，称为渐进时间复杂度。

公式中，高阶对于增长趋势影响最大，所以低阶、常数、系数可以忽略。
上面两个例子忽略之后：
(3n + 3 ) unit_time 时间复杂度为 O(n)。
(2 * n^2 + 3n + 3) * unit_time 时间复杂度为 O(n^2)。

如何分析时间复杂度？

只关心循环执行最多的一段代码，这段代码是最高阶量级，对增长趋势影响最大。
上面两个例子代码：
(3n + 3 ) unit_time 时间复杂度为 O(n)。
(2 * n^2 + 3n + 3) * unit_time 时间复杂度为 O(n^2)。

加法法则：不同代码段取最高阶量级。

int func(int n) 
{int sum_1 = 0; //1 * unit_timefor (int p = 1; //1 * unit_timep < 100;    //100 * unit_time++p)        //100 * unit_time{sum_1 = sum_1 + p;  //100 * unit_time}//上面一段求sum_1代码时间复杂度为：302 * unit_timeint sum_2 = 0;//1 * unit_timefor (int q = 1; //1 * unit_timeq < n;  //n *  unit_time++q)    //n *  unit_time{sum_2 = sum_2 + q; //n *  unit_time}//上面一段求sum_2代码时间复杂度为：(3n + 2) * unit_timeint sum_3 = 0;//1 * unit_timefor (int i = 1; //1 * unit_timei <= n;     //n *  unit_time++i)        //n *  unit_time{for (int j = 1; //n *  unit_timej <= n;     //n^2 *  unit_time++j)        //n^2 *  unit_time{sum_3 = sum_3 + i * j;//n^2 *  unit_time}}//上面一段求sum_3代码时间复杂度为：(3n^2 + 3n + 2) * unit_timereturn sum_1 + sum_2 + sum_3;//1 * unit_time
}

三段代码时间复杂度求和为最高阶：O(n^2)。

总结： T1(n)=O(f(n))，T2(n)=O(g(n))； 那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n)))

乘法法则：嵌套代码，嵌套内外代码复杂度的乘积。

int func(int n) 
{int num = 0;    1 * unit_timefor (int i = 1; //1 * unit_timei <= n;     //n *  unit_time++i)        //n *  unit_time{for (int j = 1; //n *  unit_timej <= n;     //n^2 *  unit_time++j)        //n^2 *  unit_time{fun(n, num);//n^3 *  unit_time}}
}int fun(int n, int num)
{for (int k = 1; //1 * unit_timek <= n;     //n *  unit_time++k)        //n *  unit_time{num++;      //n *  unit_time}
}

func 函数执行时间复杂度为：O(n^2) * O(n) = O(n^3)

总结：T1(n)=O(f(n))，T2(n)=O(g(n))；那么 T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n))

常见时间复杂度量级有哪些？

O(1)

代码执行时间不随数据规模 n 增大而增大，时间复杂度都为O(1)。

int func(int n) 
{int sum = 0;    //1 * unit_timefor (int p = 1; //1 * unit_timep < 100;    //100 * unit_time++p)        //100 * unit_time{sum = sum + p;  //100 * unit_time}
}

O(logn)

下面代码：

int func(int n) 
{int i = 1;while (i <= n) {i = i * 2;}
}

i 取值为等比数量，每一次取值：

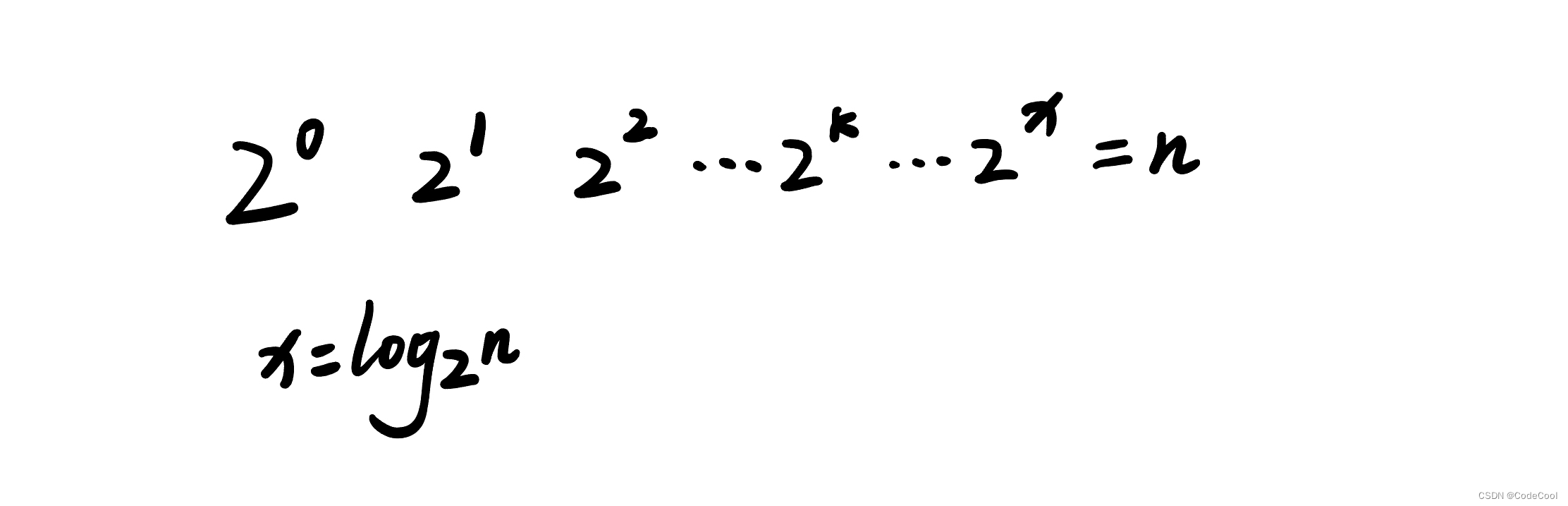
代码修改：

int func(int n) 
{int i = 1;while (i <= n) {i = i * 3;}
}

i 取值为等比数量，每一次取值：

对数阶时间复杂度中，忽略对数的 “底”，同意表示为O(logn)。

O(nlogn)

将对数嵌套在循环中：

int func(int n) 
{int i = 1;for (int j = 0; j < n; ++j){while (i <= n){i = i * 2;}}
}

O(m+n)、O(m*n)