2023.11.2

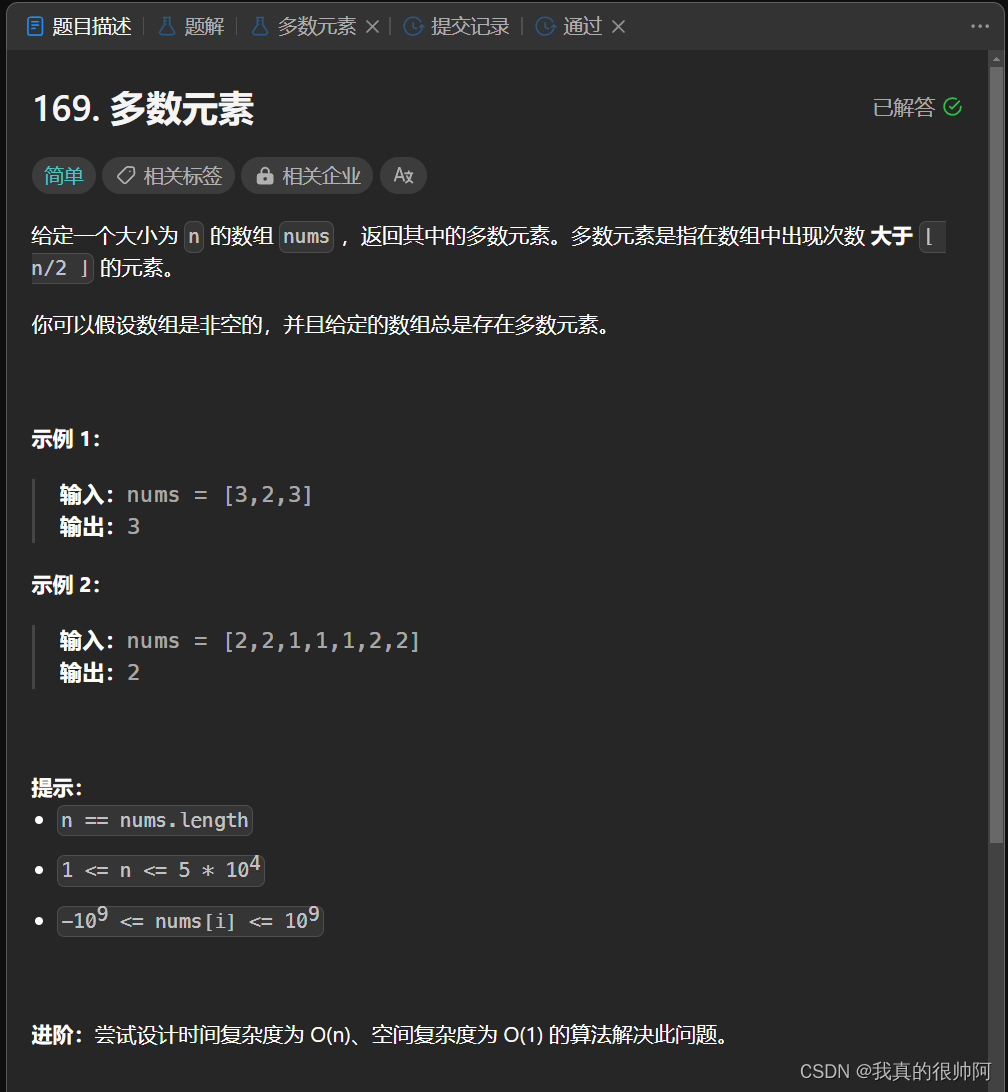
        本题我的思路是将数组nums中的元素以及其出现次数保存至一个哈希表hashMap中，然后找到哈希表中大于⌊n/2⌋ 的value值，并返回对应的key即可。 java代码如下：

class Solution {public int majorityElement(int[] nums) {Map<Integer,Integer> hashMap = new HashMap<>();for(int i=0; i<nums.length; i++){int v = hashMap.getOrDefault(nums[i],0) + 1;hashMap.put(nums[i],v);}Set<Map.Entry<Integer,Integer>> entries = hashMap.entrySet();for(Map.Entry<Integer,Integer> entry : entries){int v = entry.getValue();if(v > nums.length / 2) return entry.getKey();}return 0;}
}