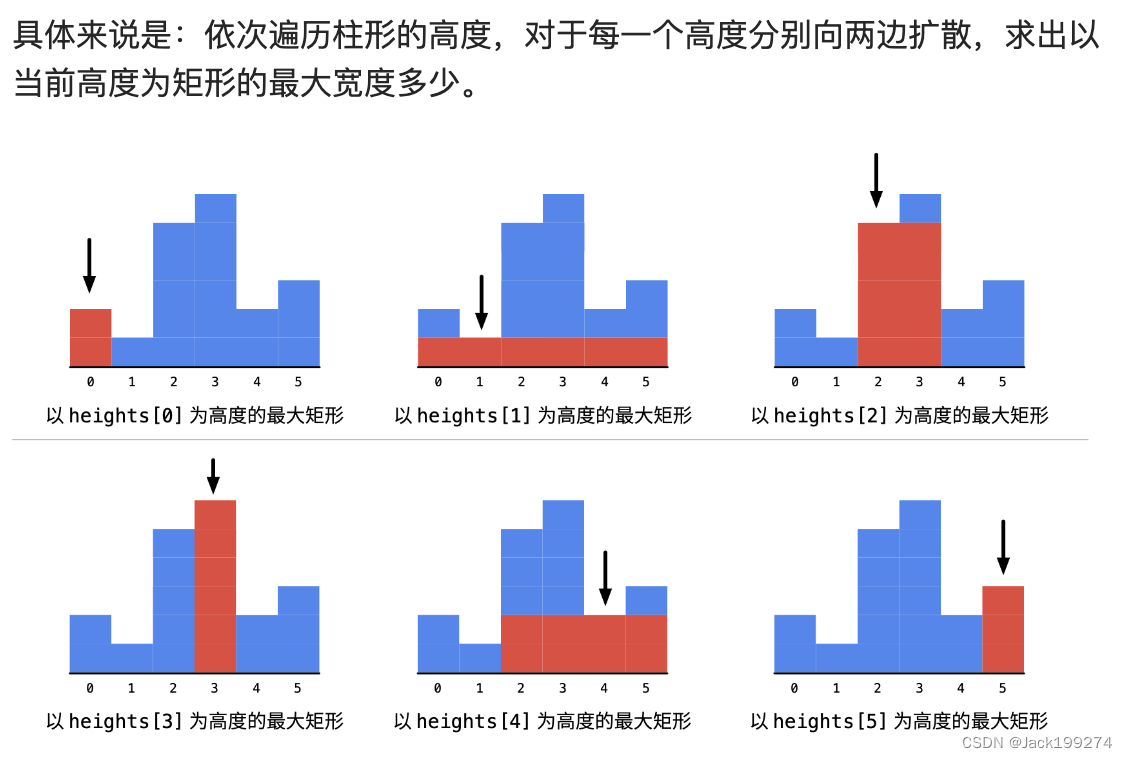
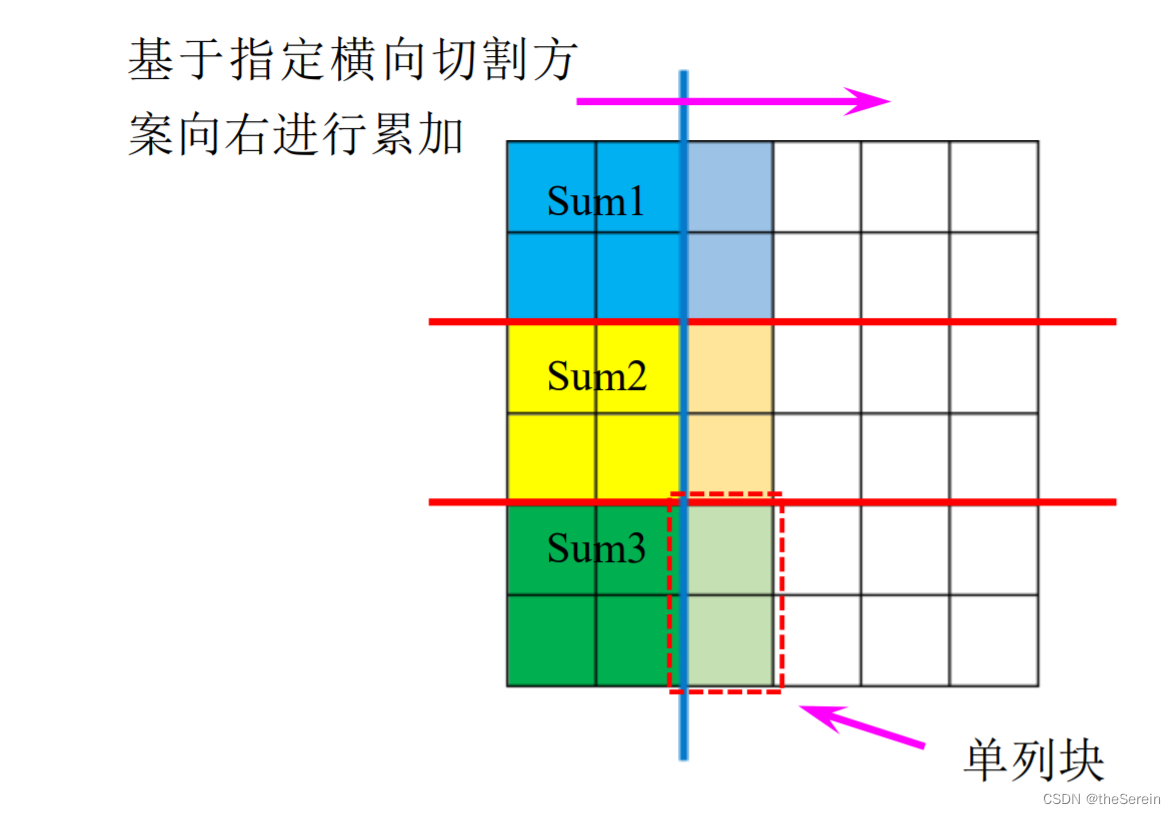
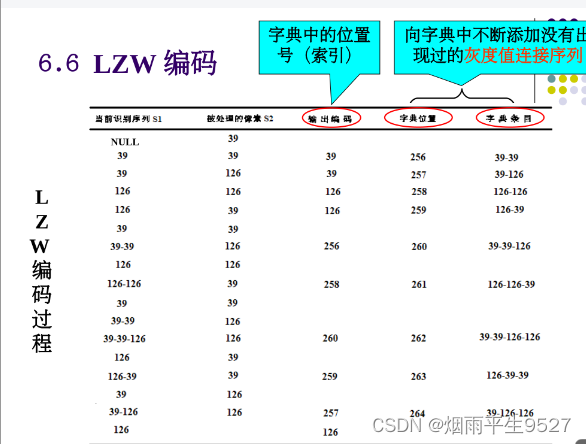
回归问题,例如之前做房子价格预测的线性回归问题
而softmax回归是一个分类问题,即给定一个图片,从猫狗两种动物类别中选出最可靠的那种答案,这个是两类分类问题,因为狗和猫是两类
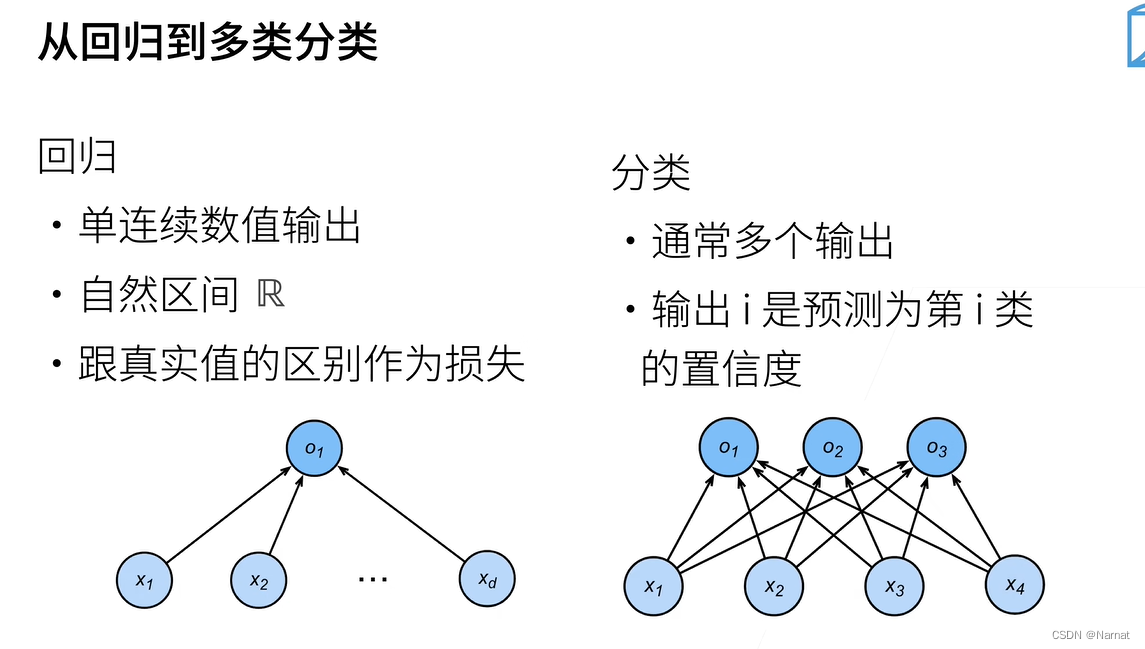
上述多个输出可以这样理解,假设一个图片让机器辨别这个图片的类别,假设是三类分类问题,分别是猫,狗,鸟,那么机器对图片分析假设会得出这样一个置信度的输出即[0.6, 0.3, 0.1]可以看出猫的置信度比较高为0.6,那么机器会判别这个图片为猫

继续拿上述猫狗鸟进行举例,那么y(注意这里不是小写y)可以是 [猫, 狗, 鸟]
假设上述让机器检测的图片就是猫,那么y1 = 1,其他都是0
即[1, 0, 0]
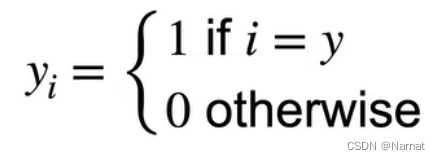
这其中的y就是被检测图片真实类别的标号

机器能对图片真实类别检测生成的置信度高于其他类别生成的置信度即可,朴素的来讲,只要机器识别这个图片是猫的概率比识别为其他动物的概率高即可

这里的exp是e的意思,即指数能化负数为正数,且这样算最后所有概率的和为1即上述0.6 + 0.3 + 0.1 =1

为什么要用这个交叉熵损失呢,好处在哪呢?
例如:

那么梯度是如何求出来的呢?

求法如下:
由于:

所以:
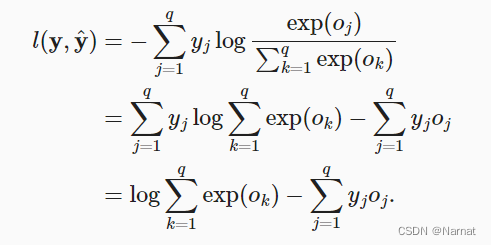
求偏导oj如下:
注:exp是以e为底的意思,log在计算机中一般都是以e为底

一些理解:
对于不同的损失函数其梯度也会有所差异:
对于均方误差其梯度与预测值真实值的区别为:
梯度的方向总是指向减小损失的方向,即使是小步骤的调整也可以减小误差。
所以,均方误差的梯度告诉我们如何调整模型的预测值,以使损失函数减小,即更接近真实值。
对于交叉熵损失函数:
梯度是真实概率和预测概率之间的区别