在金融市场中，优化投资组合对于实现风险与回报之间的预期平衡至关重要。蒙特卡罗模拟提供了一个强大的工具来评估不同的资产配置策略及其在不确定市场条件下的潜在结果。

我们的目标是开发一个蒙特卡罗模拟模型的投资组合优化。参与者将被要求构建和分析由各种资产类别(例如，股票，债券和另类投资)组成的投资组合，以最大化预期回报，同时管理风险。

数据

我们从Kaggle的找到乐资产价格数据，使用CSV文件进行分析。也可以使用yfinance在固定的时间内(b/w开始和结束日期)获得实时股票价格。

然后重点分析了由于多种因素导致的股票“调整后收盘价”。数据的“调整后收盘价”部分是指市场收盘前最后一个交易价格的现金价值。调整后的收盘价归因于任何可能影响当天市场收盘后股价的因素。

调整后的收盘价有助于投资者了解公司行动宣布后股票的公允价值，也有助于保持股票价格开始和结束的准确记录，因此我们选择对其进行分析，而不是收盘价。

我们还需要更深入地了解正在使用的股票之间的关系，以及一个股票的变化如何影响另一个股票。这将有助于投资者分散投资组合，从而将风险降至最低。分散投资很重要，因为当市场下跌时，它可以帮助投资者，因此一些股票可能会抵消其他资产所造成的损失。所以绘制了协方差和相关性的热图

Seaborn的pairplot()函数用于创建散点图矩阵。在这个矩阵中，可以看到stock_returns中的变量是如何成对关联的。由此得出的图表可以让我们深入了解不同公司日收益之间的相关性和模式。

使用下面代码生成一个热图来可视化stock_returns与在所提供的代码段中创建的相关矩阵之间的相关性。

对数收益率和简单收益率

我们通常更喜欢对数收益率而不是收益率。因为它是时间可加的，并且它服从正态高斯分布

我们还可以从对数回报的直方图中看到，它大多以0为中心，看起来有点正态分布。

但这里有一个相当棘手的问题:对于金融数据来说，正态分布是一个好的假设吗?

我们先假设价格或更准确的对数回报是正态分布的。

可以看到，偏差很大，在正态分布中，99.75%的数据在3个标准差以内，而这里不是这样。但是我们如何检验正态性以及如何将其近似为高斯分布。

可以看到，通常将金融数据视为正态分布在大多数情况下是一个不错的假设（除了尾部）。从上图中我们也可以看到，头部和尾部都偏离了正态。

我们还可以证明对数收益是可加的，通过观察当我们将整个过程的对数收益相加，我们得到收盘价。

从上面的代码片段中看到，log的结果准确地预测了它。但是如果我们使用简单收益率，

这些简单的收益率虽然给出了实际值的预测，但不是实际值，因为正态分布变量的乘积不是正态分布的。

简单移动平均线(SMA)

采用移动平均线以消除波动并减少数据中存在的变化数量。这个过程称为时间序列平滑。

可以使用10、20、30天移动平均线，短移动平均线通常用于短期交易，而长移动平均线则用于长期交易。

当我们考虑更多的天数时，这条线变得越来越平滑。所以当考虑更多的天数时，这条线对波动的滞后性就会更大。

计算收益和分配

下面代码片段计算数据列表中每个公司的日收益，并使用直方图可视化这些收益的分布。

我们看到它几乎遵循正态分布，我们说“几乎”，因为在直方图的头部和尾部(我们对其进行了平滑以得出这个结论)并不严格遵循正态分布

随机股票，组合和最大夏普比率

我们这里有一个randomPortfolio()的函数，该函数负责生成一个随机的股票组合。

它通过从标准正态分布中提取随机值，对其取幂以确保其为正值，然后将其规范化以表示总投资组合价值的比例，从而生成随机的股票投资组合。通过调用这个函数，可以为投资组合获得随机分配的股票。

收入组合(Rand)和风险组合(Rand)。这些函数被设计用来执行与投资组合的收入和风险相关的计算。

IncomePortfolio(Rand)函数根据平均收入值和资产配置计算投资组合的预期收入。

RiskPortfolio(Rand)函数根据收益和资产配置的协方差矩阵计算投资组合的风险。

这些函数为评估投资组合的收益和风险特征提供了基本的度量。

将变量“组合”初始化为10000。这个变量决定了将要生成和评估的投资组合的数量

接下来创建三个名为“risk”、“income”和“portfolio”的数组，并将它们初始化为零。这些数组将存储每个组合的风险、收益和投资组合数据。

然后将随机生成的投资组合分配到“投资组合”数组的第i行。“投资组合”数组中的每一行代表不同的股票组合。

调用“RiskPortfolio()”函数，将当前的投资组合作为参数传递。此函数计算与给定投资组合相关的风险。然后使用当前投资组合作为参数调用“IncomePortfolio()”函数。该函数计算投资组合的收益或预期收益。

该比率是指每单位波动率或总风险的平均收益超过无风险利率。波动性是衡量资产或投资组合价格波动的指标。

无风险收益率是指零风险投资的回报，也就是说，这是投资者在不承担风险的情况下所期望的回报。

最优风险投资组合是夏普比率最高的投资组合。

通过在其相应的风险和收益值上添加一个红点，使用一个图例来识别最大夏普比率。散点图直观地表示了投资组合的风险和收益关系。

最佳投资组合是具有最大夏普比率的投资组合，其权重也可以提取的。

该代码标识夏普比率最高的投资组合，然后显示分配给该投资组合中每个公司的分配或权重。使我们能够看到资产或公司在最佳表现的投资组合中是如何分配的。

使用蒙特卡罗模拟未来的价格预测

所提供的代码片段引入了一个名为monte_carlo的函数，该函数使用蒙特卡罗方法来模拟股票的未来价格。

对于随机路径的生成，这里使用了算术布朗运动，也可以使用几何布朗运动。

算术布朗运动

方差越大，价差越大，陡峭度越小。

在蒙特卡罗模拟的前提下，如果方差较小，生成的随机路径将较少微分，如果方差较大，则产生更平坦的曲线，则生成的随机路径将更多。

monte_carlo函数使用蒙特卡罗方法生成指定天数的模拟股票价格。它考虑了初始股票价格、平均日收益和日收益的标准差。该函数结合随机冲击和漂移组件来计算每天的模拟价格。

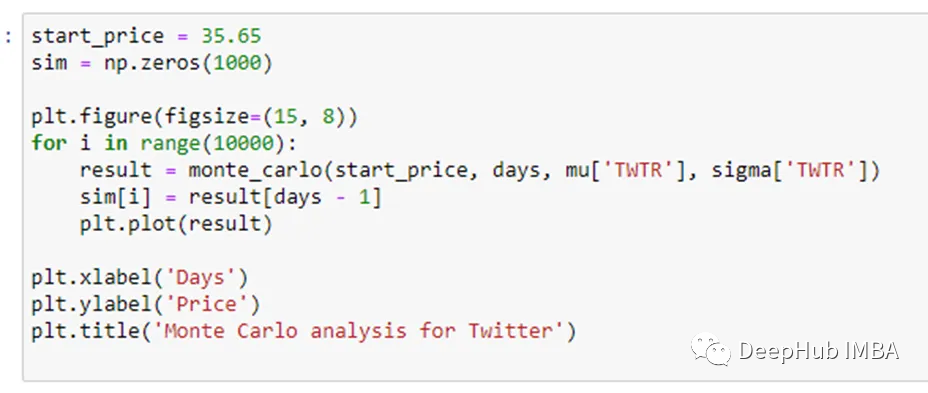
这段代码通过1000次模拟来预测Twitter的未来价格，从而对Twitter的股票进行蒙特卡洛分析。这些模拟的最终价格存储在“sim”数组中并绘制出来。通过这样做，代码提供了对Twitter股票未来价格范围的潜在洞察，这是由蒙特卡洛模拟确定的。

所提供的代码构造了一个直方图来说明从蒙特卡洛模拟中得到的Twitter股票模拟价格的分布。可视化包括概述模拟价格的平均值、标准偏差和初始价格的文本注释。根据蒙特卡洛模拟，这种可视化表示为Twitter未来股价的潜在范围和特征提供了有价值的见解。

下一步工作

我们上面只是简单进行了蒙特卡罗模拟，如果想深入研究，还可以进行以下工作：

1、采用Q-Q图(如上所述)、箱形图、Kolmogonov Smirmov测试等正态性度量来量化正态性，这将有助于可视化量化数据的正态性。

2、使用指数移动平均线(EMA)， EMA的计算强调最近的数据点。EMA对价格变化的反应比简单移动平均线(SMA)更快。

3、在计算移动平均线时考虑的天数的影响及其对平滑的影响。

4、使用Sortino Ratio、M2 Ratio、Calmar Ratio等其他风险回报指标，并对其差异进行校正，根据场景选择最合适的风险回报指标。

5、利用几何布朗运动(GBM)代替算术布朗运动(ABM)生成随机路径，将随机路径输入到蒙特卡罗仿真中。观察改变风险因素如何影响最优投资组合。

本文代码：

https://avoid.overfit.cn/post/9d7e2c80f7464d0b94b364e3d53f64be

作者：Aman Behera