24张宇八套卷复盘（五）

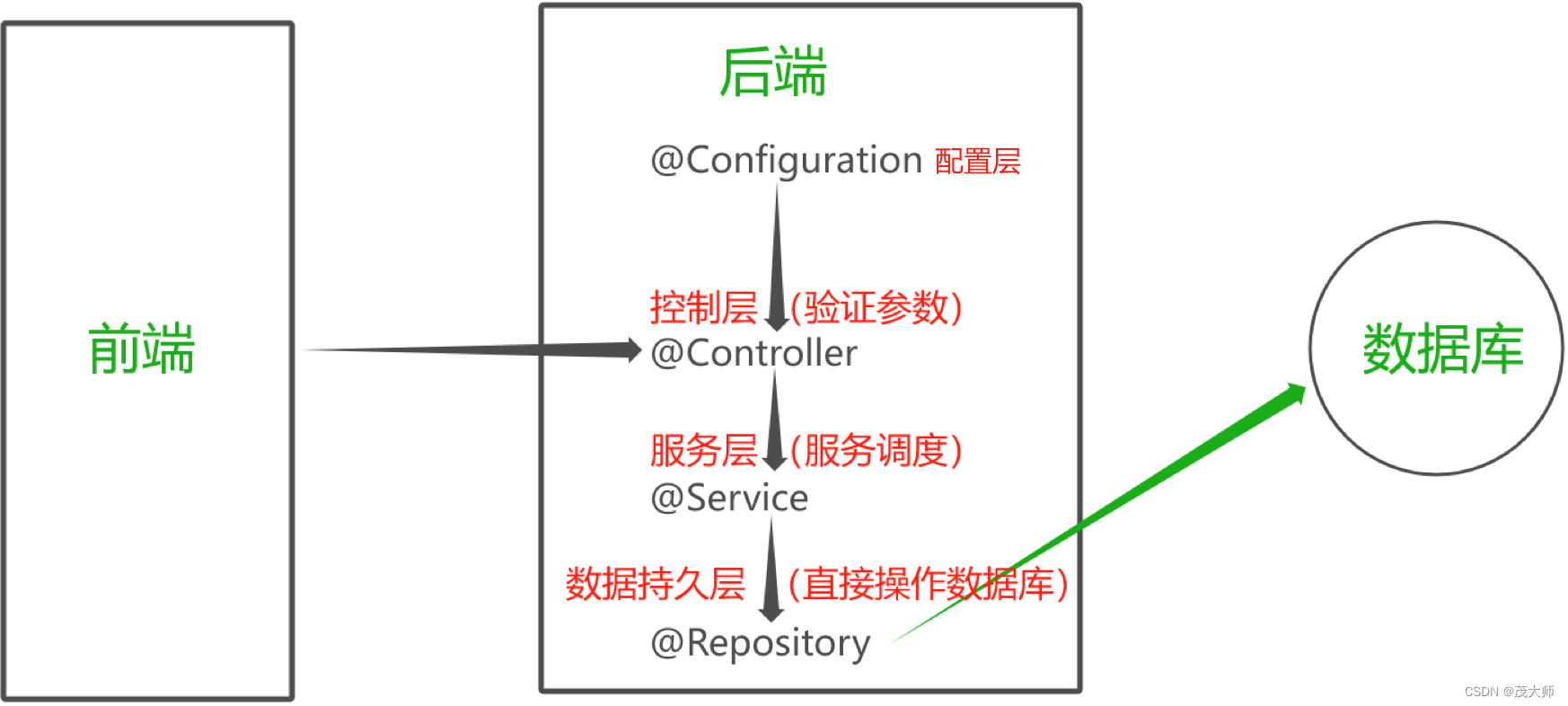
张八（）	94
选择	25
填空	20
高数大题	25
线代大题	12
概率大题	12

前言

临近考试冲刺阶段，感觉做过的卷子很难再提起精神去复盘，于是在这里进行一下复盘。

主要是对于整体试卷结构的把握，以及考试状态的复盘。

简单的卷子把会做的做对争取高分，难一点的卷子反思下次如果碰到它怎么获得更多的分数。

其次是复习遗忘了的解题技巧或者知识点，对于答案都看不太懂的部分，我选择性跳过，在这个阶段很难再吸收什么技巧，张八里这种题可能每年都有一两个地方。所以这个复盘只能说是自用的，后期临考前方便对整个试卷进行再把握。

试卷结构评析

第五套选择题难度飙升，直接错了五个。以第1题为例，它考的肯定不算难把，但是综合的太多了，极限计算，间断点定义，绝对值，但凡漏了一步就寄了。第二题一个等于和等价的区别，90%的人都要错，但别觉得不应该，恰恰是错才正常。

填空14出的真的比23年大题的计算量都多两倍

压轴应该是18的第二问，技巧性很强，但不偏，很有挑战。然而我就不挑战了，随缘。

19题压在极值定义这一个知识点有点不合适了，改成一道中值常规题，这套试卷的结构就完美了。当然难度还是感觉比真题大许多了。

考试状态复盘及策略

第2题理解题意花了一定时间

第6题从选项入手验证花了大量时间

第8题没搞出来

第9题独立相关的判断也把我搞蒙了

第10题公式列的很对，但是不知道n是常数。整体选择都花了50分钟了

选择感觉全是漏洞

填空第14第一遍直接空了

第15不会因式分解，勉强看出来是1/2E

第16思路也不是很清晰，还在想统计量X拔的性质。

第18第二问以为算出来了

第19极值定义那里找到f（0，y）=f（0，0），以为不是极值点，现在也不知道为啥是极值点。

第20第一问关系没找明白，一开始算的P是定点，重新算才算对了。

第21读题，想题花了不少时间，然后尝试配方花不少时间，最后做出来。

第22比较顺利。

最后写完之后检查一遍选填，把14题算了，但遗憾的是算错。其他的改动的点是第6题又验证了大量时间改对了，9，16改了答案，但是都还是错的，总结是基本功还需精进。

策略：这套明显是比第一套难上许多，策略方面其实没啥好说的，因为并没有因为纠结于某一道题。这套考的是基本功。

对于检查方法，有必要更进一下。对于第1题这种问的是可去间断点，就扣字眼，先判断你找的点是不是间断，再判断是不是可去。

实际上考试不会有这么多难以确定的题目，对于难以确定的题目，第二遍检查时可以在思考角度停留的久一些，比如第9题跳出题设去想判断独立的方法，第16题去想让求什么，是统计量又不一定要用统计量的性质，乱写容易混乱导致计算出错或想错。

第一题

这里提醒我了对于三角型函数无穷小的一种处理方法，对于当x→0时，sinΠx，令Πx=t，转换为t→0，sint→0，然后再用等价无穷小即可。对于当x→1时，sinΠx，令x-1=t，这就又转换为了当t→0时，sinΠt→0，这时再用上述的替换或者直接泰勒麦克劳林公式都行。
这题除了考极限外，还考了间断点的定义，我倒在了这一步，首先x=0是可去算出来了，然后发现只有x=1时它不是无穷间断，我直接下结论选B了，事实上这里因为绝对值的缘故，这是个跳跃间断点，题目问的是可去间断点。
破局的方法有两个，一个是注意到题目问的是可去，那么你就必须算到底，先看看是不是间断，再看看是不是两端极限一致；其次注意到有绝对值，绝对值很容易引起跳跃，然后再注意到题目问的是可去间断点。

第二题

扣字眼了，没有注意到是考 = 和 ~ 的区别，于是把①②选上了
这道题其实还可以，挺能考察无穷小阶的概念，虽然考的不深。但是埋的坑有点刻意了，等号是等价的区别是个人都知道，但考场能不能注意到真是看运气了，十道完型填空直接没了。

第三题

折腾一番后从选项入手也能发现a=e时恰好发散，然后我想的是指数越大那么函数值越大，这里又是正项级数，那肯定更发散。
实际上这里是减函数，恰恰相反，教训是以后不能想当然，指数越大函数值又不一定更大，要看一下单调性
这题标准做法是考的大纲新加入的积分判别法，非负连续且单调减少就可以等同于反常积分叛敛，令t=lnx的手法也值得学习

第四题

可以直接令f(x)=1/2,看一下没问题后就选C
这里想考一个定积分换元把，注意定积分的几何意义，1到2的图像面积加3到4的图像面积恰好是一个周期。

第六题

这里考了一个施密特正交化，已经背不住了，感觉没必要背
这里前后至少花了20分钟，思路就是把矩阵乘法写好，把选项答案一个一个代入，把D选出来。

第七题

一开始还把二次型矩阵写出来了，感觉不对劲。然后发现先用可逆线性变化换为y1y2，然后再换成(z1-z2)(z1+z2) 即可,可逆线性变换就是合同变换，不改变正负惯性指数

第八题

这里一开始就是想用概率的归一性，但是算无穷级数求和时不小心把减去第0项搞成加1了，然后算出a→无穷，就没继续想了
然后又想到P{X＜Y}=P{X＞Y}，就选了A，但是又困惑于X=Y的概率是0吗？然后选了A不再纠结。
很关键的一步是把X=Y的概率用无穷级数表示出来P{X=k，Y=k}，然后再自然地想到独立分开乘，再用无穷级数求和。

第九题

这里混淆了独立性的条件，只有离散型是用P{X=k，Y=k}=P{X=k}P{Y=k}，以为是独立的，于是一定不相关。
相关性就用COV的期望公式算，这里由于X和Y换元后都是三角函数，XY也是三角函数，有周期性，期望肯定是0，于是不相关
独立性要看概率密度相乘是不是联合概率密度，只能先求出边缘概率密度。

第十题

这里列了个式子，n(ap+b-1)+(1-p)b=0,一开始以为n，p都是变量，算不出结果，这里应该是一个方程一个未知数，于是a，b，n都是常系数。我认为这题应该再描述一句n为常数。这一点困扰了我太久
注意审题，题目的意思是p可变，n是确定的。那么式子应该改写为 p(an-b)+nb-n+b=0，于是令an-b=0，即可得出答案。

第十一题

同第一题，答案喜欢直接洛必达
我习惯是这里三角函数的无穷小问题，可以直接令x-1=t，然后再三角恒等变形即可。

第十四题

图像应该是一个斜着的球面的一部分，这一部分大概是球体在三分之一切一刀，三分之一个球面的部分，切的那个底的半径是根号3
错误做法：由于图像是斜的，I表达式是轮换对称的，相当于可以把球面掰正，~~于是只有zdxdy了~~，然后用二型面直接投。这里想当然了，其他两个面也有投影。
答案做法：补面用高斯，对于高斯后的区域，可以掰正，然后先一后二；对于补的那个切一刀的面，先算出单位法向量，然后转换到一型面，然后代入边界方程x+y+z=根3

第十五题

没有看出来怎么因式分解，但是看了一会看出来A=1/2E，这时应该马上写出因子（E-2A），然后再因式分解，避免漏解

第十六题

这里写出来概率密度，求谁的期望就把谁乘概率密度积分
这里其实跟统计量没啥关系，就是一个求期望，写的有点混乱多带了个n。

第十七题

注意不要出现二阶导，答案有一步用了中值定理，我觉得那一步直接洛必达也行

第十八题

这里想考一个夹逼，这题的思路真的超出我的极限了，没法解释。有点像根据答案出题。
不过还是能得到一些经验，对于积分类题目第二问求极限，可能没告诉你考夹逼，要自己试出来。
这题的技巧性也很强了，首先是在一个周期上做文章，这一点值得学习。然后发现先算出来S(nΠ)和S(n+1pai)的值，我觉得根据这个值才能知道下面要除什么。
因此思路就是
大概率是要用夹逼👉出现周期函数，大概率是要在一个周期上用夹逼👉左右两端的值可以算出来，因为一会要夹住，所以我先算出来👉除以相应的系数让左右两端夹住👉惊奇地发现和所求形式一样。

第十九题

第一问泰勒展开有一项的系数搞错了，导致结果不对
第二问答题卡都写满了，发现判别式为0，充分判别法失效，然后就击中盲点，对于这种情况的处理我不是很清楚
这里有点疑问，f（0，y）显然属于去心邻域，但它又是0，等于f（0，0），不满足极值点定义了。

第二十题

这里主要是一个符号问题，定t的范围时先找两个点，然后看看两个点在图中的位置和题干的从哪个点到哪个点，就可以判断t的范围了。
答案斯克托斯公式的话还要画图确定投影，感觉这个图不是很好画，参数法找两个点就行。

第二十一题

这里降低难度了，是二阶，然后有一项是2 $X_{1}X_{2}$ ，所以可以配方的方式就两种，第一种不行，第二种我就直接往答题卡上开始写了。
之所以跟答案不一样，因为我写的是y2对的x1，这一点无所谓，我当时想到答案可能是y1对x1了。
答案的做法是一种通法：就是对于f，先把它化为规范形，对于g，也使用这个变换，那么就化成一种另一个合同二次型，然后再对g进行正交变换化为标准形（其实这里可逆线性变换也能将g化为标准形），但注意为啥必须用正交变换呢？其实这里是为了让 f 的规范形（对称阵是对角阵）通过这个正交变换再化为规范形（特征值不变）。