向量点乘、叉乘的概念和意义

一、向量点乘（内积）

点乘（Dot Product）的结果是点积，又称数量积或标量积（Scalar Product）。

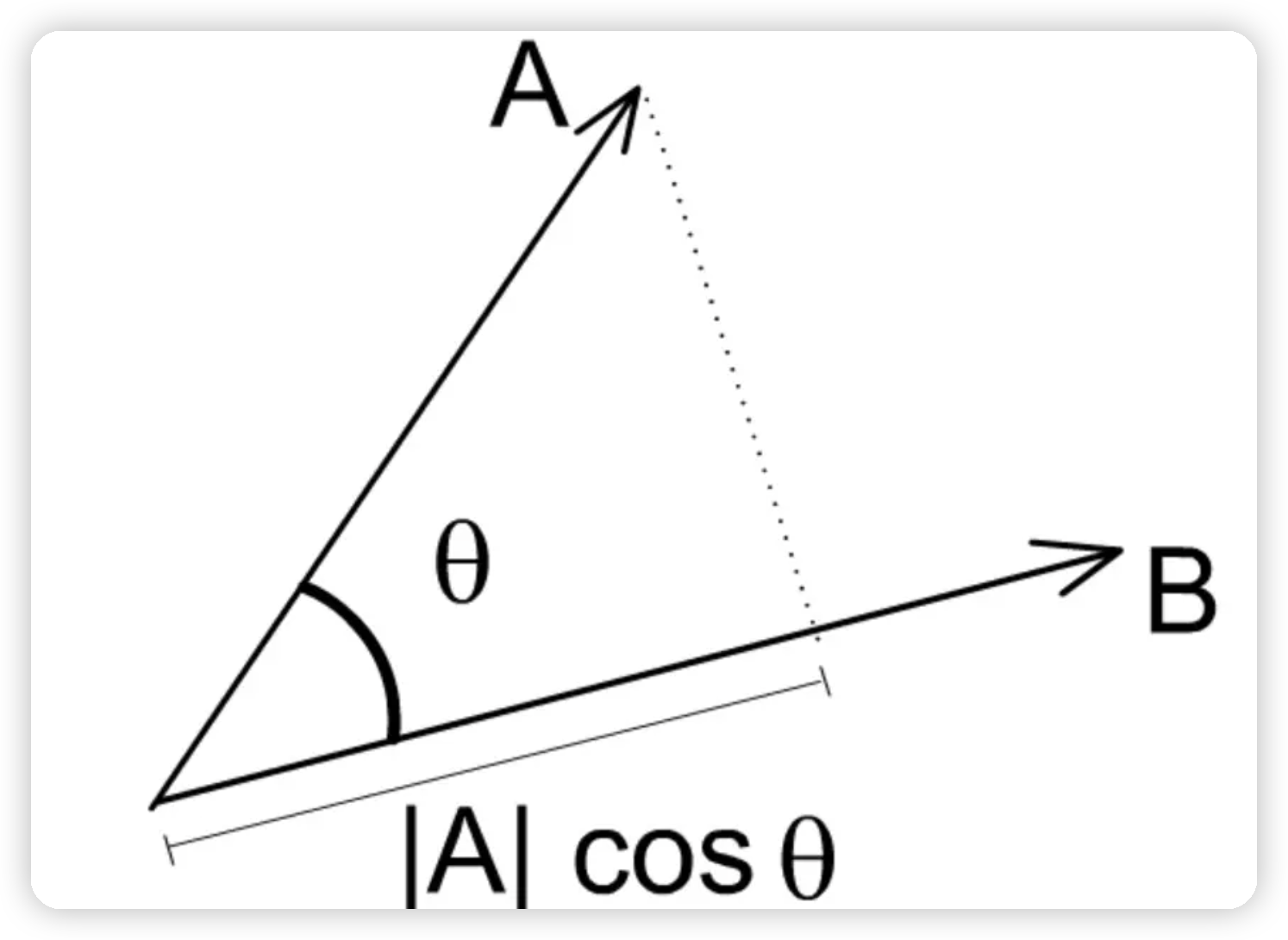
1.1 几何意义

1.2 点乘的代数定义，推导几何定义（用于求向量夹角）

1.2.1 余弦定理

余弦定理

1.3 程序计算

vector1 = [1.1, 2.2, 3.3]
vector2 = [4, 6, 7]
dot_product = np.dot(vector1, vector2) # 算向量内积
norm1, norm2 = np.linalg.norm(vector1), np.linalg.norm(vector2) # 算向量模长
similarity = dot_product / (norm1 * norm2) # 算向量间的余弦相似度

向量的内积也被称为点积，是两个向量相乘的一种方式。对于两个n维的向量，比如向量a=(a1, a2, …, an)和向量b=(b1, b2, …, bn)，它们的内积可以通过以下公式计算：

a·b = a1b1 + a2b2 + … + an*bn

这个公式表示的是将两个向量对应位置的元素相乘，然后将所有的乘积相加。结果是一个标量，而不是一个向量。

这个计算在很多领域都有重要应用，比如在物理学中，力的内积可以用来计算功，而在计算机科学中，内积常常被用于计算向量的相似度。

package main
import ("fmt""math"
)func vectorMagnitude(vec []float64) float64 {sum := 0.0for _, v := range vec {sum += v * v}return math.Sqrt(sum)
}func main() {vec := []float64{1, 2, 3}fmt.Println("Magnitude of the vector:", vectorMagnitude(vec))
}

二、向量叉乘（外积）

叉乘（Cross Product）又称向量积（Vector Product）

2.1 几何意义

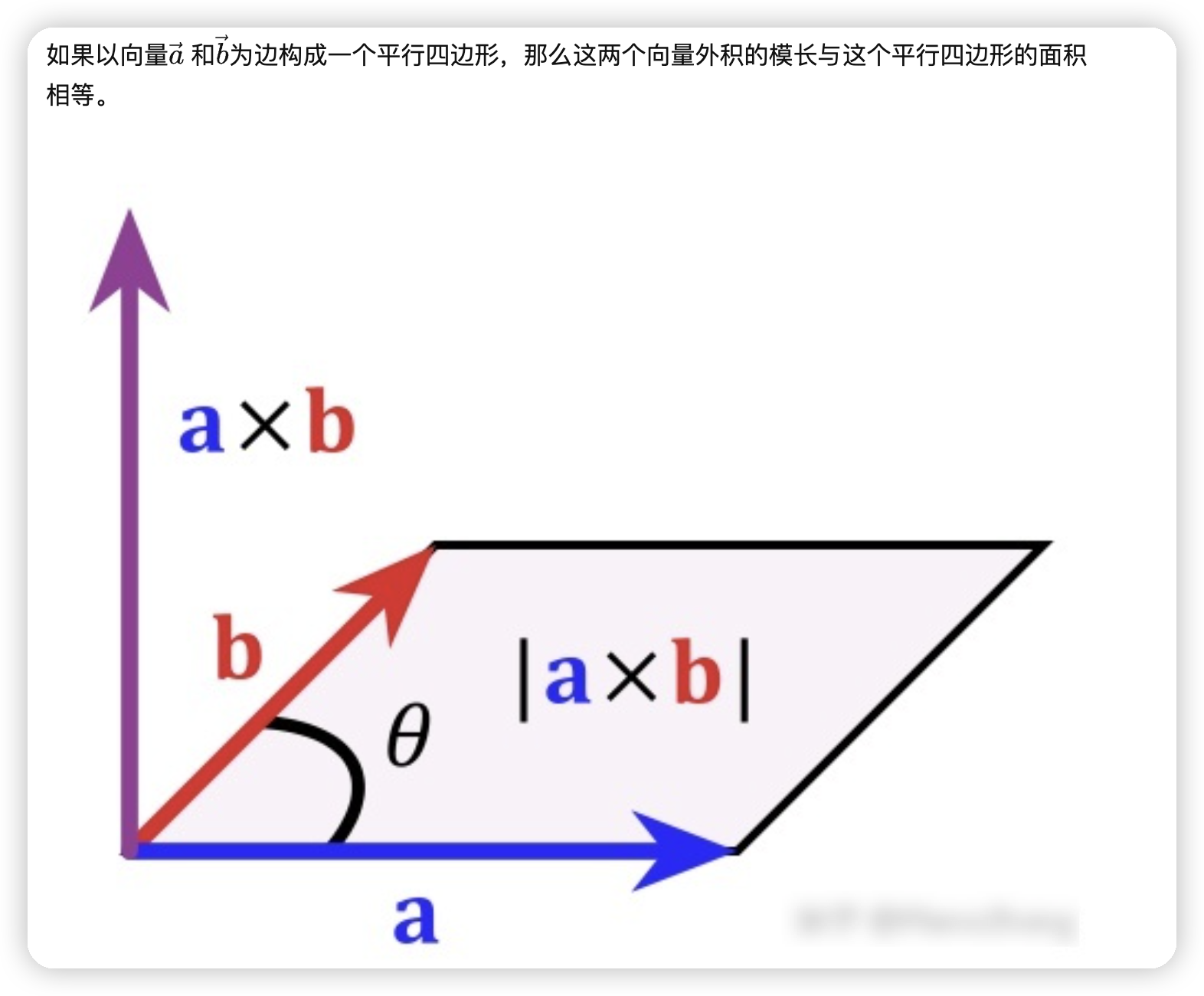
三、通俗理解内积和外积

内积是把a向量投影到b向量上面，让两者同向或者反向，让a向量箭头指向b向量里面，所以叫内积，（非官方，本人感受，同直线情况广义指向内里），外积是把a向量投影到b向量的法线方向，所以你看，投影完箭头指向了b向量的外面，所以你看透彻理解多重要，字面意思就都理解了有木有，另外，内积两个向量谁投影谁都没关系，因为最后是一个数值，不影响结果，外积就不一样了，一定是1投影2，因为要用右手确定结果3向量的方向，有前后顺序之分，更像是1带2的扭矩方向的感觉

四、向量的模长

向量的模长，也被称作向量的大小或者绝对值，是用来描述向量的长度的数学概念。在二维平面上，一个向量可以被视作箭头或者线段，而向量的模长就是箭头或线段的长度。在高维空间中，虽然我们无法直观地看到向量，但是我们仍然可以通过计算来得到向量的模长。

对于一个n维向量v = (v1, v2, …, vn)，其模长||v||可以通过以下公式计算：

$||v||=sqrt(v{1}^2+v{2}^2+...+v{n}^2)$

这里的sqrt表示平方根函数。所以，向量的模长实际上就是其各分量平方和的平方根。