目录
1 概率路线算法简介
2 代码解析
3 路径规划算法总结
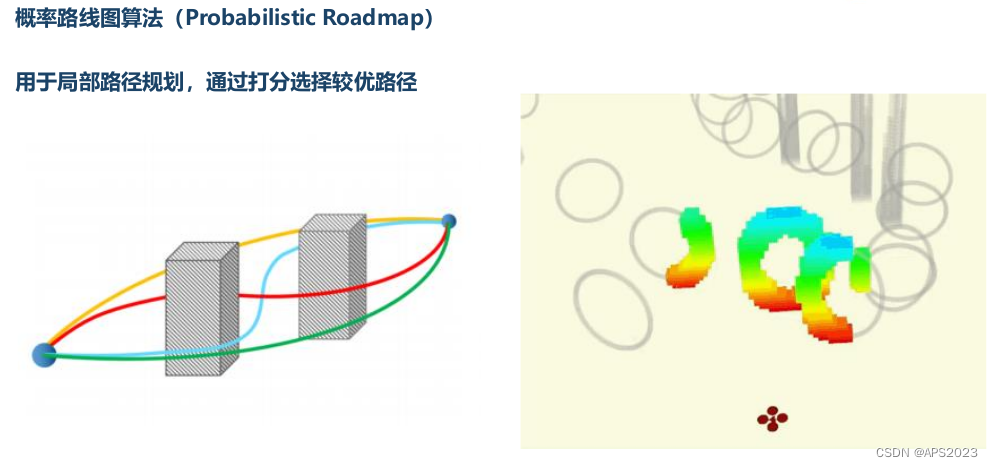
1 概率路线算法简介
它属于采样算法里面的一类。主要步骤分为两步:
1.构建概率路线图
(1)随机采样点
(2)将新采样点和距离小于阈值的 采样点连接产生图2.在图上寻找路径
(1)Dijkstra算法
(2)A*算法刚开始有起点、终点两个点作为初始化的采样点:
我们开始随机采样:
进行连接。再采样再连接:
如果采样点有障碍物,我选择不连接:
我们继续采样,我们简单的举例:
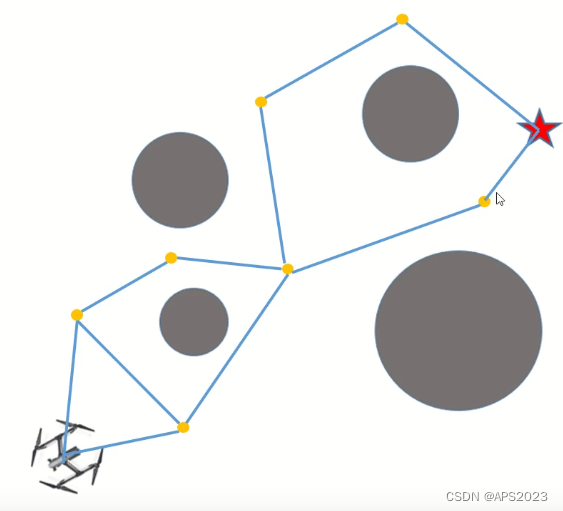
这样我们就建立了一个图了,我们再通过Dijkstra算法或者A*算法来做路径规划。
缺点是:这个是两阶段算法,速度较慢且没法寻找最优路径。
可以用作局部路径规划:
2 代码解析
先来看一下运行结果:
我们首先还是定义了起点坐标终点坐标以及障碍物的坐标。
规划的主函数如下:
# start xy goal xy 障碍物xy 机器人大小 def prm_planning(sx, sy, gx, gy, ox, oy, rr):obstacle_kd_tree = cKDTree(np.vstack((ox, oy)).T)sample_x, sample_y = sample_points(sx, sy, gx, gy,rr, ox, oy, obstacle_kd_tree)if show_animation:plt.plot(sample_x, sample_y, ".b")road_map = generate_road_map(sample_x, sample_y, rr, obstacle_kd_tree)rx, ry = dijkstra_planning(sx, sy, gx, gy, road_map, sample_x, sample_y)return rx, ryobstacle_kd_tree = cKDTree(np.vstack((ox, oy)).T):这行代码是用于构建一个k维树(kd-tree)的数据结构,以便于在二维空间中高效地查找最近邻的障碍物。具体来说,它使用了一个名为
cKDTree的函数来构建kd-tree。
np.vstack((ox, oy)).T:
ox和oy是一些障碍物的x和y坐标的数组。np.vstack用于垂直堆叠(将数组按垂直方向拼接在一起),((ox, oy)).T表示将这个堆叠后的矩阵进行转置,以保证每一行代表一个点,每列代表一个维度(在这里是x和y坐标)。
cKDTree():
- 这是一个用于构建kd-tree的函数,它接受一个二维数组作为输入,这个数组中的每一行代表一个点,每列代表一个维度。
假设你有以下障碍物的坐标:
ox = [1, 2, 3, 4, 5] oy = [1, 2, 3, 4, 5]那么,通过执行以下代码:
obstacle_kd_tree = cKDTree(np.vstack((ox, oy)).T)将会得到一个名为
obstacle_kd_tree的kd-tree数据结构,该结构会根据障碍物的坐标构建一个高效的查找树。你可以使用这个kd-tree来进行最近邻的搜索,例如查找离一个给定点最近的障碍物。比如,如果你想找到离点
(3, 3)最近的障碍物,你可以使用以下代码:nearest_obstacle_index = obstacle_kd_tree.query([3, 3])[1] nearest_obstacle = (ox[nearest_obstacle_index], oy[nearest_obstacle_index]) print(nearest_obstacle)这将会输出离点
(3, 3)最近的障碍物的坐标,也就是(3, 3)。我们再来看随机取样函数:
def sample_points(sx, sy, gx, gy, rr, ox, oy, obstacle_kd_tree):max_x = max(ox)max_y = max(oy)min_x = min(ox)min_y = min(oy)sample_x, sample_y = [], []while len(sample_x) < N_SAMPLE:tx = (random.random() * (max_x - min_x)) + min_xty = (random.random() * (max_y - min_y)) + min_ydist, index = obstacle_kd_tree.query([tx, ty])if dist >= rr:sample_x.append(tx)sample_y.append(ty)sample_x.append(sx)sample_y.append(sy)sample_x.append(gx)sample_y.append(gy)return sample_x, sample_y首先计算了障碍物坐标的最大最小值,以确定随机采样点的范围。创建了两个空列表sample_x和sample_y,用于存储采样到的点的x和y坐标。使用一个循环来生成随机点,直到采样到足够数量的点(N_SAMPLE)为止。每次循环中,随机生成一个点(tx, ty),并使用kd-tree查询该点附近的最近障碍物距离和索引。
random.random()返回一个大于等于0且小于1的随机浮点数。在上述代码片段中,random.random()被用于生成一个随机的横坐标tx和纵坐标ty,以便在地图上随机采样点。这样可以在地图范围内均匀地选取随机点,以便进行路径规划。road_map = generate_road_map(sample_x, sample_y, rr, obstacle_kd_tree)def generate_road_map(sample_x, sample_y, rr, obstacle_kd_tree):"""Road map generationsample_x: [m] x positions of sampled pointssample_y: [m] y positions of sampled pointsrr: Robot Radius[m]obstacle_kd_tree: KDTree object of obstacles"""road_map = []n_sample = len(sample_x)sample_kd_tree = cKDTree(np.vstack((sample_x, sample_y)).T)for (i, ix, iy) in zip(range(n_sample), sample_x, sample_y):dists, indexes = sample_kd_tree.query([ix, iy], k=n_sample)edge_id = []for ii in range(1, len(indexes)):nx = sample_x[indexes[ii]]ny = sample_y[indexes[ii]]if not is_collision(ix, iy, nx, ny, rr, obstacle_kd_tree):edge_id.append(indexes[ii])if len(edge_id) >= N_KNN:breakroad_map.append(edge_id)if show_roadmap:plot_road_map(road_map, sample_x, sample_y)plt.plot(sample_x, sample_y, ".b")return road_map这段代码定义了一个名为
generate_road_map的函数,它用于生成一个道路图,以便后续的路径规划算法可以在其中搜索有效的路径。函数的主要功能如下:
创建了一个空列表
road_map用于存储道路图信息。计算了采样点的数量
n_sample。使用
cKDTree创建了一个kd-tree数据结构,用于高效地查询采样点。对于每一个采样点,循环执行以下操作:
- 使用kd-tree查询最近的采样点,并返回距离和索引。
- 初始化一个空列表
edge_id用于存储可以连接到当前点的其他采样点的索引。- 对于查询结果中的每一个点,检查是否与当前点可以连接而且没有碰撞。如果满足条件,将其索引加入到
edge_id列表中。- 如果已经找到足够数量(
N_KNN)的连接点,则结束循环。将
edge_id列表添加到road_map中,记录了与每个采样点相连接的其他采样点的索引。如果设定了
show_roadmap为True,则会调用一个名为plot_road_map的函数来可视化生成的道路图,并在图上绘制采样点。最后,返回生成的道路图。
最后我们用Dijkstra进行路径规划。完整代码如下:
"""Probabilistic Road Map (PRM) Plannerauthor: Atsushi Sakai (@Atsushi_twi)"""import random import math import numpy as np import matplotlib.pyplot as plt from scipy.spatial import cKDTree# parameter N_SAMPLE = 100 # number of sample_points N_KNN = 10 # number of edge from one sampled point MAX_EDGE_LEN = 30.0 # [m] Maximum edge lengthshow_animation = True show_roadmap = Trueclass Node:"""Node class for dijkstra search"""def __init__(self, x, y, cost, parent_index):self.x = xself.y = yself.cost = costself.parent_index = parent_indexdef __str__(self):return str(self.x) + "," + str(self.y) + "," +\str(self.cost) + "," + str(self.parent_index)# start xy goal xy 障碍物xy 机器人大小 def prm_planning(sx, sy, gx, gy, ox, oy, rr):obstacle_kd_tree = cKDTree(np.vstack((ox, oy)).T)sample_x, sample_y = sample_points(sx, sy, gx, gy,rr, ox, oy, obstacle_kd_tree)if show_animation:plt.plot(sample_x, sample_y, ".b")road_map = generate_road_map(sample_x, sample_y, rr, obstacle_kd_tree)rx, ry = dijkstra_planning(sx, sy, gx, gy, road_map, sample_x, sample_y)return rx, rydef is_collision(sx, sy, gx, gy, rr, obstacle_kd_tree):x = sxy = sydx = gx - sxdy = gy - syyaw = math.atan2(gy - sy, gx - sx)d = math.hypot(dx, dy)if d >= MAX_EDGE_LEN:return TrueD = rrn_step = round(d / D)for i in range(n_step):dist, _ = obstacle_kd_tree.query([x, y])if dist <= rr:return True # collisionx += D * math.cos(yaw)y += D * math.sin(yaw)# goal point checkdist, _ = obstacle_kd_tree.query([gx, gy])if dist <= rr:return True # collisionreturn False # OKdef generate_road_map(sample_x, sample_y, rr, obstacle_kd_tree):"""Road map generationsample_x: [m] x positions of sampled pointssample_y: [m] y positions of sampled pointsrr: Robot Radius[m]obstacle_kd_tree: KDTree object of obstacles"""road_map = []n_sample = len(sample_x)sample_kd_tree = cKDTree(np.vstack((sample_x, sample_y)).T)for (i, ix, iy) in zip(range(n_sample), sample_x, sample_y):dists, indexes = sample_kd_tree.query([ix, iy], k=n_sample)edge_id = []for ii in range(1, len(indexes)):nx = sample_x[indexes[ii]]ny = sample_y[indexes[ii]]if not is_collision(ix, iy, nx, ny, rr, obstacle_kd_tree):edge_id.append(indexes[ii])if len(edge_id) >= N_KNN:breakroad_map.append(edge_id)if show_roadmap:plot_road_map(road_map, sample_x, sample_y)plt.plot(sample_x, sample_y, ".b")return road_mapdef dijkstra_planning(sx, sy, gx, gy, road_map, sample_x, sample_y):"""s_x: start x position [m]s_y: start y position [m]gx: goal x position [m]gy: goal y position [m]ox: x position list of Obstacles [m]oy: y position list of Obstacles [m]rr: robot radius [m]road_map: ??? [m]sample_x: ??? [m]sample_y: ??? [m]@return: Two lists of path coordinates ([x1, x2, ...], [y1, y2, ...]), empty list when no path was found"""start_node = Node(sx, sy, 0.0, -1)goal_node = Node(gx, gy, 0.0, -1)open_set, closed_set = dict(), dict()open_set[len(road_map) - 2] = start_nodepath_found = Truewhile True:if not open_set:print("Cannot find path")path_found = Falsebreakc_id = min(open_set, key=lambda o: open_set[o].cost)current = open_set[c_id]# show graphif show_animation and len(closed_set.keys()) % 2 == 0:# for stopping simulation with the esc key.plt.gcf().canvas.mpl_connect('key_release_event',lambda event: [exit(0) if event.key == 'escape' else None])plt.plot(current.x, current.y, "xg")plt.pause(0.001)if c_id == (len(road_map) - 1):print("goal is found!")goal_node.parent_index = current.parent_indexgoal_node.cost = current.costbreak# Remove the item from the open setdel open_set[c_id]# Add it to the closed setclosed_set[c_id] = current# expand search grid based on motion modelfor i in range(len(road_map[c_id])):n_id = road_map[c_id][i]dx = sample_x[n_id] - current.xdy = sample_y[n_id] - current.yd = math.hypot(dx, dy)node = Node(sample_x[n_id], sample_y[n_id],current.cost + d, c_id)if n_id in closed_set:continue# Otherwise if it is already in the open setif n_id in open_set:if open_set[n_id].cost > node.cost:open_set[n_id].cost = node.costopen_set[n_id].parent_index = c_idelse:open_set[n_id] = nodeif path_found is False:return [], []# generate final courserx, ry = [goal_node.x], [goal_node.y]parent_index = goal_node.parent_indexwhile parent_index != -1:n = closed_set[parent_index]rx.append(n.x)ry.append(n.y)parent_index = n.parent_indexreturn rx, rydef plot_road_map(road_map, sample_x, sample_y): # pragma: no coverfor i, _ in enumerate(road_map):for ii in range(len(road_map[i])):ind = road_map[i][ii]plt.plot([sample_x[i], sample_x[ind]],[sample_y[i], sample_y[ind]], "-c")def sample_points(sx, sy, gx, gy, rr, ox, oy, obstacle_kd_tree):# 计算了障碍物坐标的最大最小值,以确定随机采样点的范围。max_x = max(ox)max_y = max(oy)min_x = min(ox)min_y = min(oy)# 创建了两个空列表sample_x和sample_y,用于存储采样到的点的x和y坐标。sample_x, sample_y = [], []# 使用一个循环来生成随机点,直到采样到足够数量的点(N_SAMPLE)为止。每次循环中,随机生成一个点(tx, ty),并使用kd-tree查询该点附近的最近障碍物距离和索引。while len(sample_x) < N_SAMPLE:tx = (random.random() * (max_x - min_x)) + min_xty = (random.random() * (max_y - min_y)) + min_ydist, index = obstacle_kd_tree.query([tx, ty])# 如果该点与最近障碍物的距离大于等于rr(即避免采样到障碍物附近),则将该点加入采样列表。if dist >= rr:sample_x.append(tx)sample_y.append(ty)# 最后,将起始点和目标点也加入到采样列表中,并返回采样到的点的x和y坐标列表。sample_x.append(sx)sample_y.append(sy)sample_x.append(gx)sample_y.append(gy)return sample_x, sample_ydef main():print(__file__ + " start!!")# start and goal positionsx = 10.0 # [m]sy = 10.0 # [m]gx = 50.0 # [m]gy = 50.0 # [m]robot_size = 1.0 # [m]ox = []oy = []for i in range(60):ox.append(i)oy.append(0.0)for i in range(60):ox.append(60.0)oy.append(i)for i in range(61):ox.append(i)oy.append(60.0)for i in range(61):ox.append(0.0)oy.append(i)for i in range(40):ox.append(20.0)oy.append(i)for i in range(40):ox.append(40.0)oy.append(60.0 - i)if show_animation:plt.plot(ox, oy, ".k")plt.plot(sx, sy, "^r")plt.plot(gx, gy, "^c")plt.grid(True)plt.axis("equal")rx, ry = prm_planning(sx, sy, gx, gy, ox, oy, robot_size)assert rx, 'Cannot found path'if show_animation:plt.plot(rx, ry, "-r")plt.pause(0.001)plt.show()if __name__ == '__main__':main()
3 路径规划算法总结
完备性:是指如果在起始点和目标点间有路径解存在,那么一定可以得到解,如果得不到解那么一定说明没有解存在。
概率完备性:是指如果在起始点和目标点间有路径解存在,只要规划或搜索的时间足够长,就一定能确保找到一条路径解。
最优性:是指规划得到的路径在某个评价指标上是最优的(评价指标一般为路径的长度)。
渐进最优性:是指经过有限次规划迭代后得到的路径是接近最优的次优路径,且每次迭代后都与最优路径更加接近,是一个逐渐收敛的过程。
规划速度:RRT系列 > A*算法 > Dijkstra算法 > 基于智能算法的路径规划算法
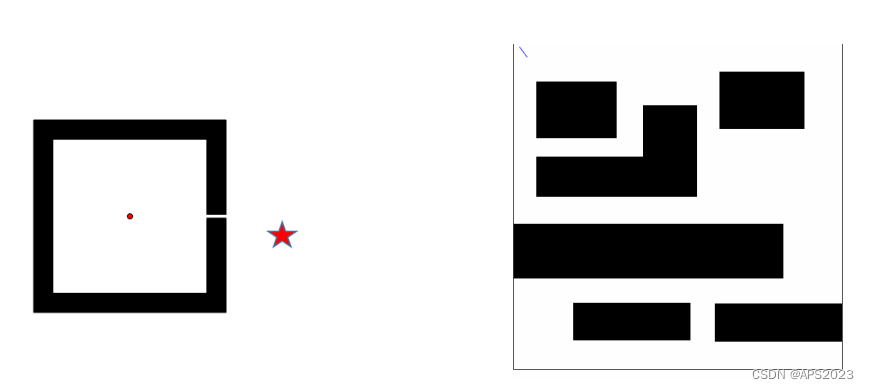
但如果是狭长路径
RRT算法会寻找非常久的时间。








![[云原生案例2.1 ] Kubernetes的部署安装 【单master集群架构 ---- (二进制安装部署)】节点部分](https://img-blog.csdnimg.cn/043e8e22185749df8d6ae3386453e179.png)