本讲是关于无人机滤波器,其中包括无人机滤波器简介、测量原理、线性互补滤波器设计、线性互补滤波器参数分析、卡尔曼滤波器设计等。
滤波器设计实验2
卡尔曼滤波器是一种递推线性最小方差估计算法,它的最优估计需满足以下三个条件:
1)无偏性:即估计值的期望等于状态的真值;
2)估计的方差最小;
3)实时性。
假设线性离散系统模型如下:
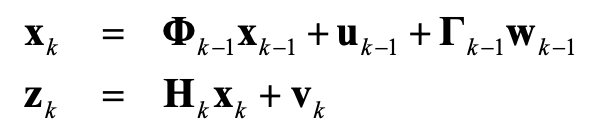
式中,过程噪声wk-1和观测噪声vk的统计特性为:
卡尔曼滤波算法可总结为如下:


卡尔曼滤波器在进行滤波器估计的同时还产生了误差协方差阵,它可以用于表征估计精度,同时也能用于传感器的健康评估。一般来说,采样周期合理情况下,连续系统可观,离散化的系统也会可观。然而有时候采样周期选择不当,系统可能失去可控性及可观性。因此原则上应该检查离散化系统的可观性。 HkPk|k-1HTk+Pk|k-1需要是H非奇异的,否则kk = Pk|k-1HTk(HkPk|k-1HTk+Pk)-1无法实现。如果(ФK,K-1,Hk) 不可观,那么卡尔曼滤波器仍然可以运行,只不过不可观的模态没有进行修正,只是递推罢了。极端情况 Hk=0m`n ,那么
卡尔曼滤波器实现见文件“Attitude_ekf.m”,其主要部分如下
function [ x_aposteriori, P_aposteriori, roll, pitch] =
Attitude_ekf( dt, z, q, r, x_aposteriori_k, P_aposteriori_k)
%函数描述:
% 状态估计的拓展卡尔曼滤波方法
%输入:
% dt: 更新周期
% z: 测量值
% q:系统噪声,r:测量噪声
% x_aposteriori_k: 上一时刻的状态估计
% P_aposteriori_k: 上一时刻估计协方差
%输出:
% x_aposteriori:当前时刻的状态估计
% P_aposteriori:当前时刻的估计协方差
% roll,pitch:欧拉角,单位: rad
w_m = z(1:3); %角速度测量值
a_m = z(4:6); %加速度测量值
g = norm(a_m,2); %重力加速度
% w_x_=[ 0,-(wz-bzg, wy-byg;
% wz-bzg, 0 ,-(wx-bxg);
% -(wy-byg), wx-bxg, 0];
w_x_ = [0, -(w_m(3) - x_aposteriori_k(3)), w_m(2) -x_aposteriori_k(2);
w_m(3) - x_aposteriori_k(3), 0, -(w_m(1) - x_aposteriori_k(1));
-(w_m(2) - x_aposteriori_k(2)), w_m(1) - x_aposteriori_k(1), 0];
bCn = eye(3, 3) - w_x_*dt;
% 预测
% 更新先验状态矩阵
x_apriori = zeros(1, 6);
x_apriori(1: 3) = x_aposteriori_k(1 : 3); %角速度漂移
x_apriori(4 : 6) = bCn*x_aposteriori_k(4 : 6); %加速度归一化值
%[x]x
x_aposteriori_k_x = [0, -x_aposteriori_k(6), x_aposteriori_k(5);
x_aposteriori_k(6), 0, -x_aposteriori_k(4);
-x_aposteriori_k(5), x_aposteriori_k(4), 0];
% 更新状态转移矩阵
PHI = [eye(3, 3), zeros(3, 3);
-x_aposteriori_k_x*dt, bCn];
GAMMA = [eye(3, 3)*dt, zeros(3, 3); % 噪声驱动阵
zeros(3, 3), -x_aposteriori_k_x*dt];
Q = [eye(3, 3)*q(1), zeros(3, 3);
zeros(3, 3), eye(3, 3)*q(2)];
% 预测误差协方差矩阵
P_apriori = PHI*P_aposteriori_k*PHI' + GAMMA*Q*GAMMA';
% 更新
R = eye(3, 3)*r(1);
H_k = [zeros(3, 3), -g*eye(3, 3)];
%卡尔曼增益
K_k = (P_apriori*H_k')/(H_k*P_apriori*H_k' + R);
% 状态估计矩阵
x_aposteriori = x_apriori' + K_k*(a_m - H_k*x_apriori');
% 估计误差协方差
P_aposteriori = (eye(6, 6) - K_k*H_k)*P_apriori;
% 计算滚转角和俯仰角,分别对应roll,pitch
k = x_aposteriori(4 : 6) /norm(x_aposteriori(4 : 6), 2);
roll = atan2(k(2), k(3)); % 滚转角
pitch = -asin(k(1)); %俯仰角
end
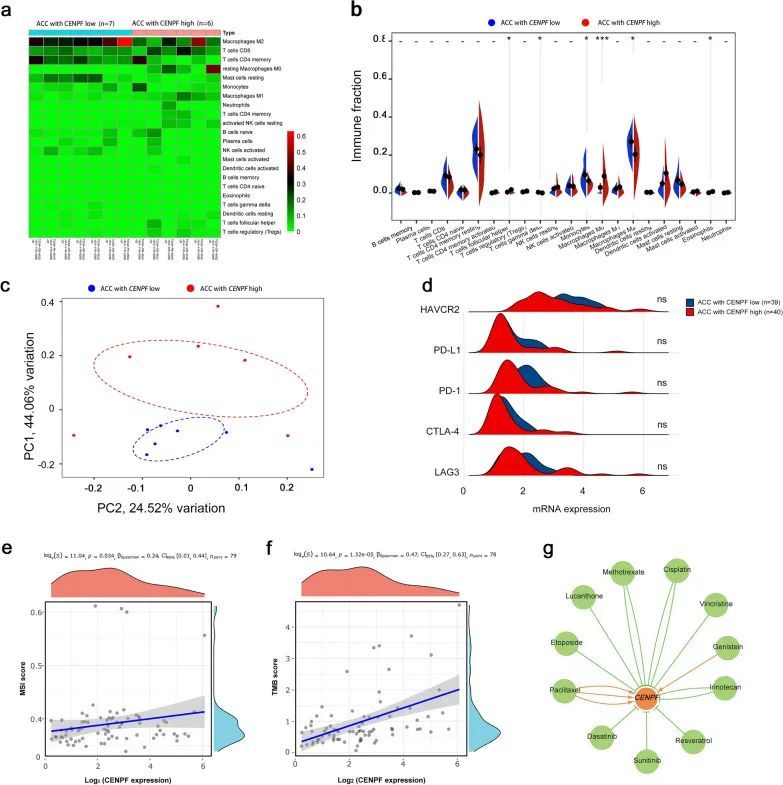
如下图所示的滤波结果及对比图。可以看到在飞行过程中,卡尔曼滤波比线性互补滤波的效果更好,与PX4自带滤波算法效果接近。
注:本实验对应demo文件对于RflySim v3.0以下版本地址为:*\PX4PSP\RflySimAPIs\Exp02_FlightControl\e4-FilterDesign\e4.3;
对于RflySim v3.0及以上版本地址为:*\PX4PSP\RflySimAPIs\5.RflySimFlyCtrl\1.BasicExps\e4-FilterDesign\e4.3。
参考文献:
[1] 全权,杜光勋,赵峙尧,戴训华,任锦瑞,邓恒译.多旋翼飞行器设计与控制[M],电子工业出版社,2018.
[2] 全权,戴训华,王帅.多旋翼飞行器设计与控制实践[M],电子工业出版社,2020.




![[vue-router]vue3.x Hash路由前缀问题](https://img-blog.csdnimg.cn/7e8e9690990a4ea28ef024c88b94e21c.png)