1. 说在前面的

之前调试基于QMI8658 6轴姿态解算的时候，我对Mahony滤波的认识还比较浅薄。初次的学习和代码的移植让我对四元数、欧拉角、旋转余弦矩阵有了一定的接触。然而，直到我将地磁传感器加入到我的硬件，进行9轴姿态解算时，我深深地感受到对四元数与姿态阵之间关系的理解是非常重要的。在此之前，我检索了网络文章，并记录了《MEMS_惯性传感器09 - Mahony姿态解算算法详解》、《MEMS_惯性传感器14 - Mahony滤波算法的代码分析》两篇文章。可能对于大佬、资深工程师来说，这些文章的严谨性不够，可能会误导别人。但我必须承认，我仍然没有扎实的数学计算研究背后更深层次的理论。即使如此，我依然希望通过自己的努力在惯性导航算法上学习得更深入一些。同时，我也想多记录一些学到的知识，多记录一些自己的理解和思考。希望这些记录能帮助到一些初学者。如果我的文章有错误的引导，我非常希望大佬们能够指正，因为这对我来说是最大的收获，我非常乐意倾听和学习。

我愿意自我突围，向着理想前进！

这次学习检索时发现了一个博文内容硬核、有理有据的博主¹路痴导航员。 她的博文 《AHRS互补滤波（Mahony）算法及开源代码》对我帮助很大。

2.Mahony滤波算法的核心思想

Mahony滤波算法的核心思想是通过将角速度和角度的测量值与历史估计值进行加权平均，从而得到更加准确的姿态估计结果。同时，滤波算法还利用加速度计的测量值来纠正姿态角度的漂移。
该算法也存在一些缺点，例如对于快速旋转和加速度变化较大的情况，其姿态估计结果可能会出现较大的误差。

3. 易懂的理解 Mahony 滤波算法的过程

为了更好的理解，表达是先不用矩阵的思想，在算法的实现的过程中，需要将表达是转换成矩阵形式。

① 根据陀螺仪的测量数据计算出角速度的增量，即：
         Δθ = 0.5 * (gyro + bias) * Δt

其中，gyro表示陀螺仪的测量值，bias表示陀螺仪的零偏误差，Δt表示时间间隔。

② 根据加速度计的测量数据计算出重力方向的估计值，即：
         g_est = q * (0, 0, -1) * q^-1

其中，q表示四元数的姿态估计值。

③ 根据加速度计的测量数据和重力方向的估计值，计算出加速度计的误差，即：
         acc_err = acc_meas - g_est

其中，acc_meas表示加速度计的测量值。

④ 根据角速度的增量和加速度计的误差，更新四元数的姿态估计值，即：
         q = q * exp(Δθ - K * acc_err)

其中，K为控制增益。

4. 其他的一些思考

• 传感器EVB板的测量数据以载体坐标系（b-框架）表示。 欧拉角的直观表示描述了地理坐标系中的角度，其中包括重力的影响。 地理坐标系中的重力矢量为[0,0,1]g，磁传感器将地球磁场中的强度表示为[cos(θ),0,sin(θ)]guess。因此，在算法中，加速度和磁数据被归一化，确保它们的模是一定大小的。

• 四元数从地理坐标系(东北天)转换到载体坐标系，就得到了旋转矩阵Cnb。
  
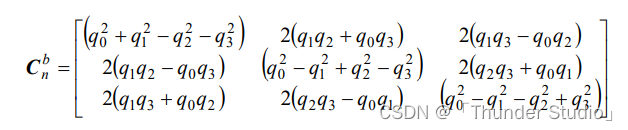
  Cnb的最后一列取负，即将其转换为载体坐标系中的值。在理想情况下，如果没有误差，这个矢量应该与测量值相等。然而，由于这两者总会存在差异，因此我们需要利用它们之间的差值来修正陀螺仪更新的不准确性。

• 在修正的过程中，我们认为加速度计测量的可信度较高，还需要使用地磁传感来修正加速度传感的Z轴。磁力计的模的长度是确定的，但是两个分量的具体大小无法像重力加速度一样确定。因此，我们使用上一次的四元数得到的Cbn（从载体到地理坐标系的旋转矩阵）来计算测量的磁场强度。理论上，此刻的Cbn应该在东向上的分量是零[cos(θ),0,sin(θ)]，而北向和地向会有分量。然而，由于此刻的Cbn尚未得到，我们使用的是上一次的Cbn，并加上一些测量误差，导致东向上仍会有分量存在。为了处理这种情况，我们将xy平面的分量合成到一个方向上，使得y轴上的分量为0。这样，处理后的地磁信息的地位就与重力加速度（0，0，-1）相似了。

• 根据余弦矩阵和欧拉角的定义，我们可以将地理坐标系的重力向量转换到载体坐标系中。具体而言，将四元数转换成方向余弦矩阵后，我们可以得到方向余弦矩阵的第三列的三个元素，即vx、vy和vz。这三个元素实际上表示了当前欧拉角（即四元数）在载体坐标系上换算得到的重力单位向量。

vx = 2*(q1q3 - q0q2);
vy = 2*(q0q1 + q2q3);
vz = q0q0 - q1q1 - q2q2 + q3q3;

• ax\ay\az是载体坐标参照系上，加速度计测出来的重力向量。vx\vy\vz是陀螺积分后的姿态推算出的重力向量。它们之间的误差向量ex\ey\ez是陀螺积分后的姿态和加计测出来的姿态之间的误差。误差向量可以用向量叉积来表示。叉积向量ex\ey\ez位于载体坐标系上，且其大小与陀螺积分误差成正比，可用于纠正陀螺。由于陀螺是对机体直接积分，所以对陀螺的纠正量会直接体现在对载体坐标系的纠正。

exInt = exInt + ex * Ki * halfT;
eyInt = eyInt + ey * Ki * halfT;    
ezInt = ezInt + ez * Ki * halfT;
// 用叉积误差来做PI修正陀螺零偏
gx = gx + Kpex + exInt;gy = gy + Kpey + eyInt;
gz = gz + Kp*ez + ezInt;

矢量之间的叉乘公式为err = A × B = |A| × |B| × sin(β)。当两个矢量重合时，误差为零，表示没有差异。当两个矢量之间夹角为90°时，误差达到最大值，表示差异最大。然而，在夹角为90°附近的区间内，误差的变化是非线性的，这可能导致一些准确性问题。

5. 民间 9轴评估板

QMI8658+QMC5883L 链接

---

1. 路痴导航员： ↩︎