目录
一、线性回归
1、回归的概念(Regression、Prediction)
2、符号约定
3、算法流程
4、最小二乘法(LSM)
二、梯度下降
梯度下降的三种形式
1、批量梯度下降(Batch Gradient Descent,BGD):
2、随机梯度下降(Stochastic Gradient Descent,SGD):
3、小批量梯度下降(Mini-Batch Gradient Descent,MBGD):
梯度下降与最小二乘法比较
梯度下降:
最小二乘法:
数据归一化/标准化
为什么要标准化/归一化?
归一化(最大 - 最小规范化)
Z-Score标准化
需要做数据归一化/标准化
不需要做数据归一化/标准化
三、正则化
1、过拟合和欠拟合
2、过拟合的处理
3、 欠拟合的处理
4、正则化
四、回归的评价指标
一、线性回归
1、回归的概念(Regression、Prediction)
- 如何预测上海浦东的房价?
- 未来的股票市场走向?
线性回归(Linear Regression)是一种通过属性的线性组合来进行预测的线性模型,其目的是找到一条直线或者一个平面或者更高维的超平面,使得预测值与真实值之间的误差最小化。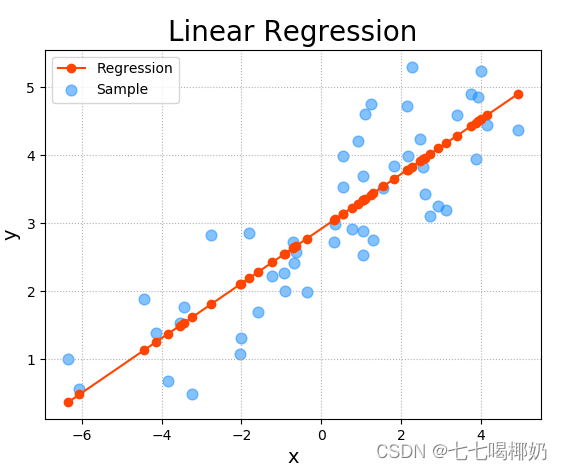
2、符号约定
- m 代表训练集中样本的数量
- n 代表特征的数量
- x 代表特征/输入变量
- y 代表目标变量/输出变量
- (x,y) 代表训练集中的样本
- (x^(i),y^(i)) 代表第i个观察样本
- ℎ 代表学习算法的解决方案或函数也称为假设(hypothesis)
- ̂┬y=ℎ(x),代表预测的值
建筑面积
总层数
楼层
实用面积
房价
143.7
31
10
105
36200
162.2
31
8
118
37000
199.5
10
10
170
42500
96.5
31
13
74
31200
……
……
……
……
……
x^(i)是特征矩阵中的第i行,是一个向量。
x_j^(i)代表特征矩阵中第 i 行的第 j 个特征
3、算法流程
损失函数(Loss Function):
度量单样本预测的错误程度,损失函数值越小,模型就越好。常用的损失函数包括:0-1损失函数、平方损失函数、绝对损失函数、对数损失函数等。
代价函数(Cost Function):
度量全部样本集的平均误差。常用的代价函数包括均方误差、均方根误差、平均绝对误差等。
目标函数(Objective Function):
代价函数加正则化项,最终要优化的函数。
x 和 y 的关系: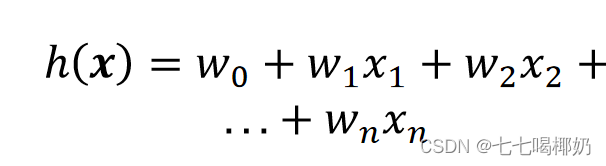
可以设x_0=1,则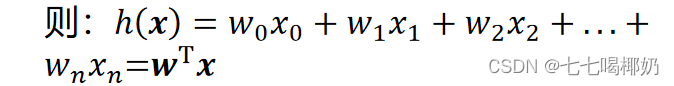
损失函数采用平方和损失: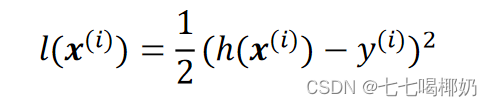
要找到一组 w(w_0,w_1,w_2,...,w_n) ,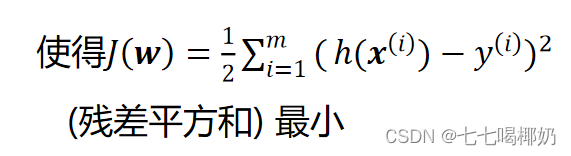
4、最小二乘法(LSM)
要找到一组 w(w_0,w_1,w_2,...,w_n) ,使得残差平方和最小。转为矩阵表达形式,令
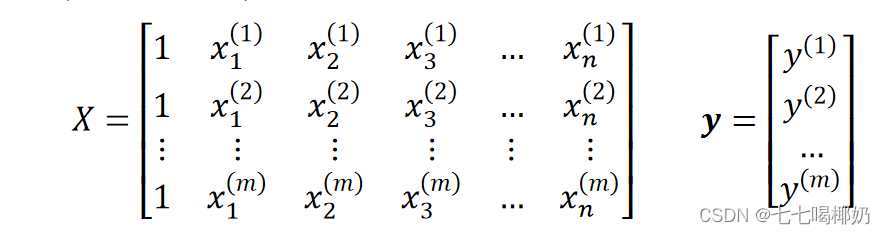
其中X为m行n+1列的矩阵(m为样本个数,n为特征个数),w为n+1行1列的矩阵(包含了w_0),Y为m行1列的矩阵,则 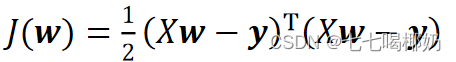
注:
(可由数学推导)
为最小化,接下来对J(w)偏导,
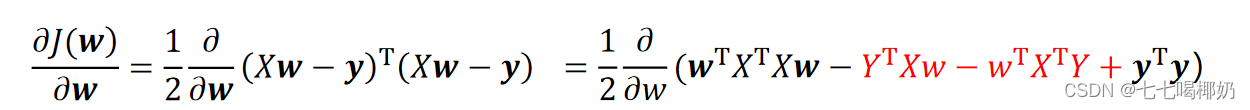
由于中间两项互为转置: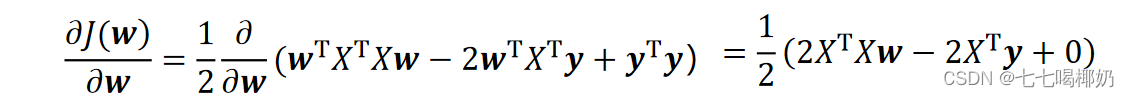
![]()
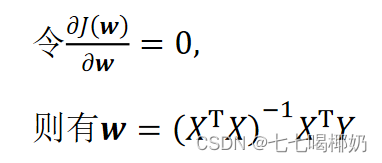
需要用到以下几个矩阵的求导结论:
二、梯度下降
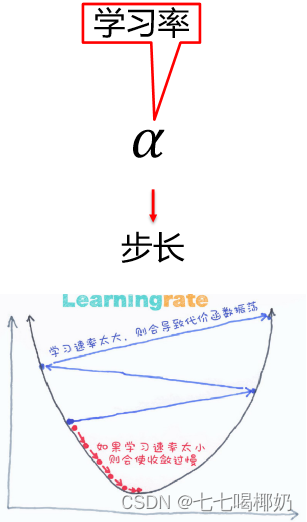
梯度下降的三种形式
1、批量梯度下降(Batch Gradient Descent,BGD):
梯度下降的每一步中,都用到了所有的训练样本

2、随机梯度下降(Stochastic Gradient Descent,SGD):
度下降的每一步中,用到一个样本,在每一次计算之后便更新参数 ,而不需要首先将所有的训练集求和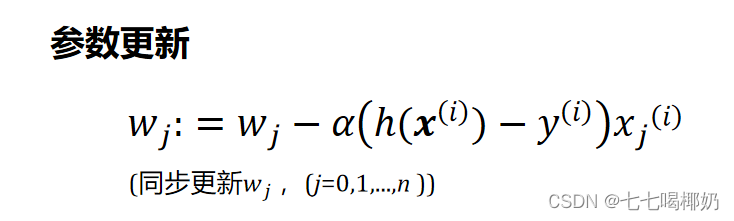
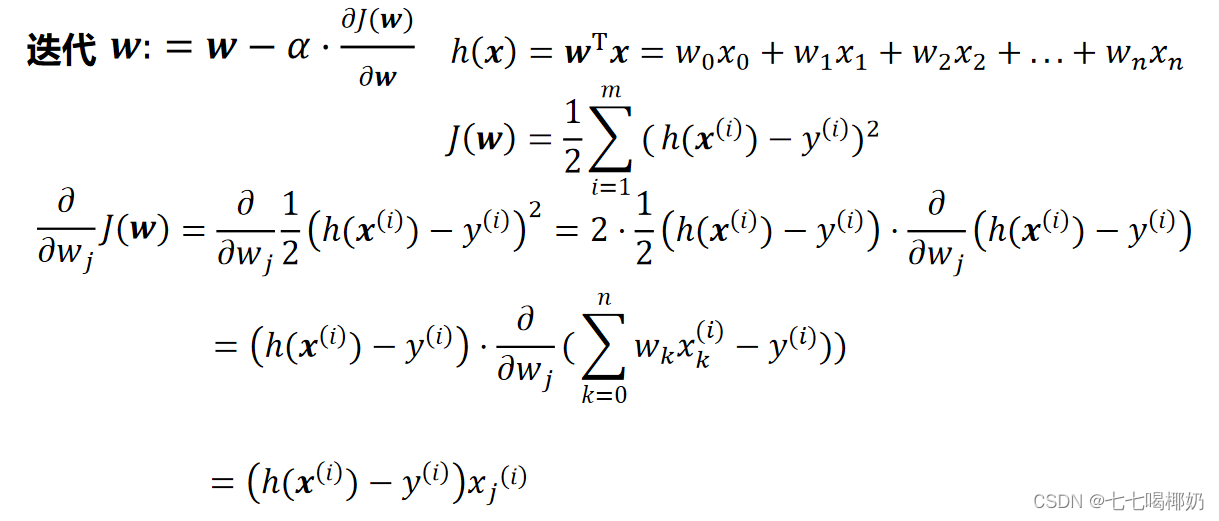
3、小批量梯度下降(Mini-Batch Gradient Descent,MBGD):
梯度下降的每一步中,用到了一定批量的训练样本
每计算常数b次训练实例,便更新一次参数 w
b=1(随机梯度下降,SGD)
b=m(批量梯度下降,BGD)
b=batch_size,通常是2的指数倍,常见有32,64,128等。(小批量梯度下降,MBGD)
梯度下降与最小二乘法比较
梯度下降:
需要选择学习率α,需要多次迭代,当特征数量n大时也能较好适用,适用于各种类型的模型。
最小二乘法:
不需要选择学习率α,一次计算得出,需要计算(X^TX)^−1,如果特征数量n较大则运算代价大,因为矩阵逆的计算时间复杂度为O(n^3),通常来说当n小于10000 时还是可以接受的,只适用于线性模型,不适合逻辑回归模型等其他模型。
数据归一化/标准化
为什么要标准化/归一化?
提升模型精度:不同维度之间的特征在数值上有一定比较性,可以大大提高分类器的准确性。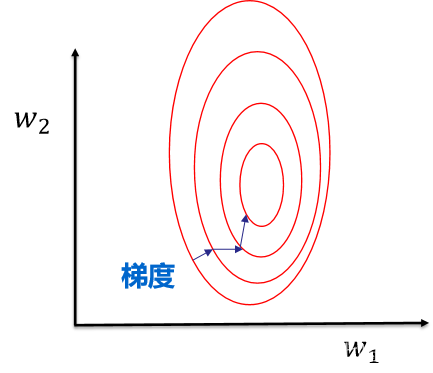
加速模型收敛:最优解的寻优过程明显会变得平缓,更容易正确的收敛到最优解。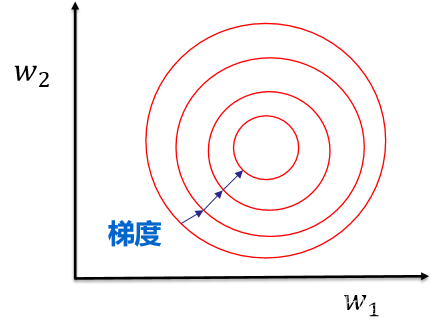
归一化(最大 - 最小规范化)
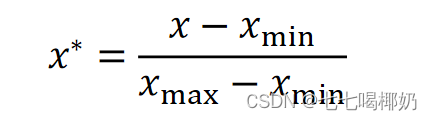
将数据映射到[0,1]区间
数据归一化的目的是使得各特征对目标变量的影响一致,会将特征数据进行伸缩变化,所以数据归一化是会改变特征数据分布的。
Z-Score标准化
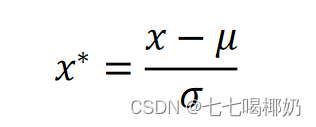

处理后的数据均值为0,方差为1
数据标准化为了不同特征之间具备可比性,经过标准化变换之后的特征数据分布没有发生改变。
就是当数据特征取值范围或单位差异较大时,最好是做一下标准化处理。
需要做数据归一化/标准化
线性模型,如基于距离度量的模型包括KNN(K近邻)、K-means聚类、感知机和SVM。另外,线性回归类的几个模型一般情况下也是需要做数据归一化/标准化处理的。
不需要做数据归一化/标准化
决策树、基于决策树的Boosting和Bagging等集成学习模型对于特征取值大小并不敏感,如随机森林、XGBoost、LightGBM等树模型,以及朴素贝叶斯,以上这些模型一般不需要做数据归一化/标准化处理。
三、正则化
1、过拟合和欠拟合
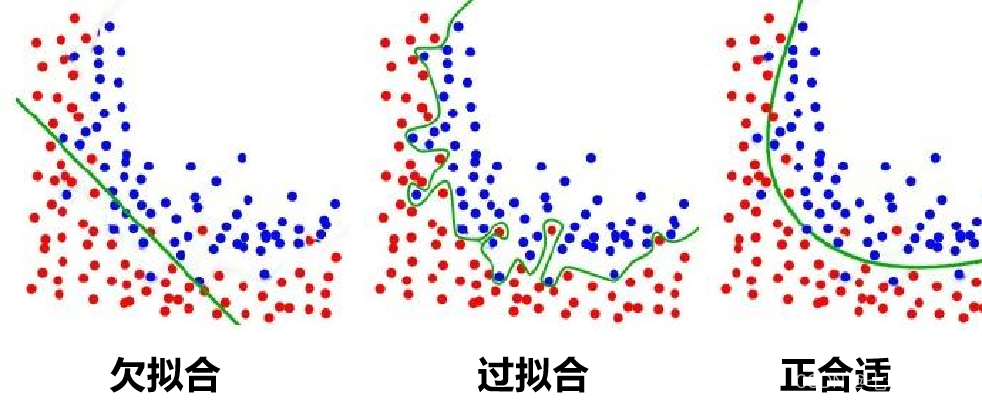
2、过拟合的处理
1.获得更多的训练数据
使用更多的训练数据是解决过拟合问题最有效的手段,因为更多的样本能够让模型学习到更多更有效的特征,减小噪声的影响。
2.降维
即丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙(例如PCA)。
3.正则化
正则化(regularization)的技术,保留所有的特征,但是减少参数的大小(magnitude),它可以改善或者减少过拟合问题。
4.集成学习方法
集成学习是把多个模型集成在一起,来降低单一模型的过拟合风险。
3、 欠拟合的处理
1.添加新特征
当特征不足或者现有特征与样本标签的相关性不强时,模型容易出现欠拟合。通过挖掘组合特征等新的特征,往往能够取得更好的效果。
2.增加模型复杂度
简单模型的学习能力较差,通过增加模型的复杂度可以使模型拥有更强的拟合能力。例如,在线性模型中添加高次项,在神经网络模型中增加网络层数或神经元个数等。
3.减小正则化系数
正则化是用来防止过拟合的,但当模型出现欠拟合现象时,则需要有针对性地减小正则化系数。
4、正则化
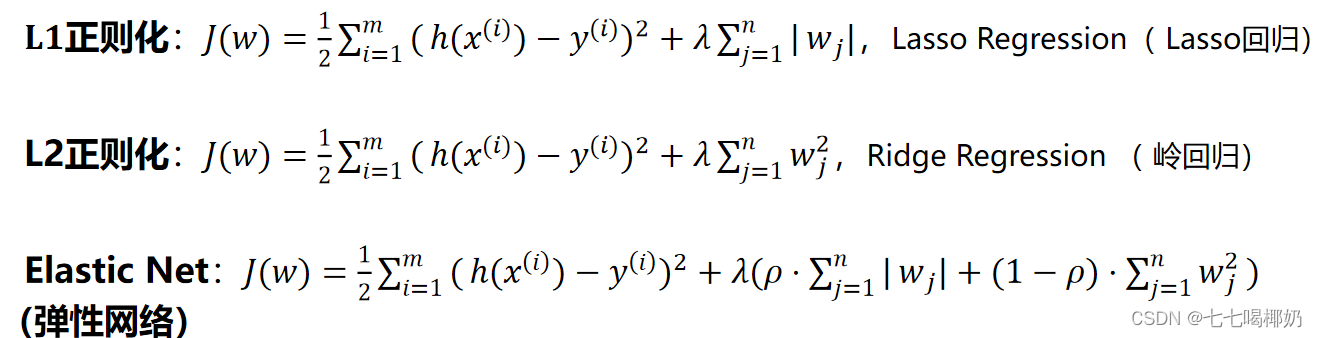
其中:
- λ为正则化系数,调整正则化项与训练误差的比例,λ>0。
- 1≥ρ≥0为比例系数,调整L1正则化与L2正则化的比例。
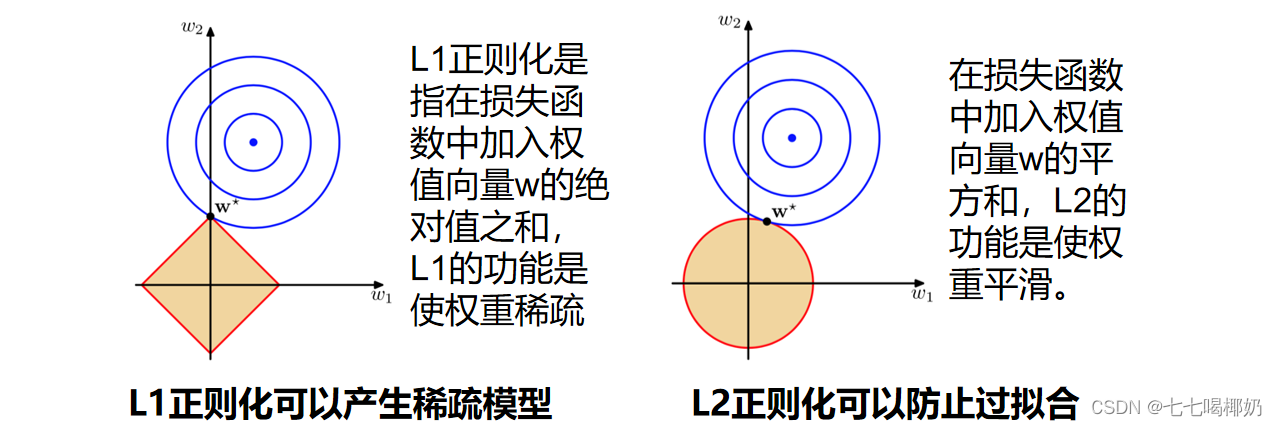
图上面中的蓝色轮廓线是没有正则化损失函数的等高线,中心的蓝色点为最优解,左图、右图分别为L1、L2正则化给出的限制。
可以看到在正则化的限制之下, L1正则化给出的最优解w*是使解更加靠近原点,也就是说L2正则化能降低参数范数的总和。
L1正则化给出的最优解w*是使解更加靠近某些轴,而其它的轴则为0,所以L1正则化能使得到的参数稀疏化。
四、回归的评价指标
均方误差(Mean Square Error,MSE)
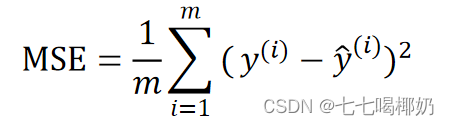
均方根误差 RMSE(Root Mean Square Error,RMSE)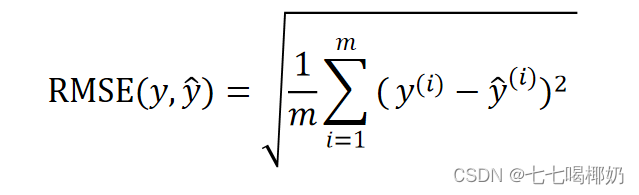
平均绝对误差(Mean Absolute Error,MAE)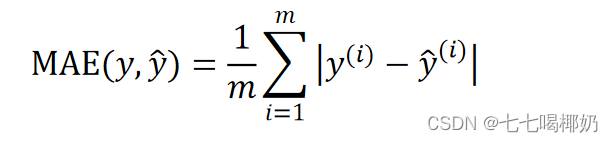

R方 [RSquared(r2score)] 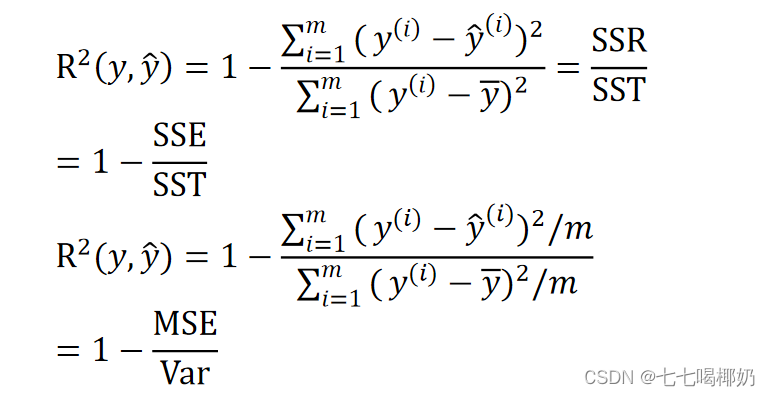
越接近于1,说明模型拟合得越好

![[unity]切换天空盒](https://img-blog.csdnimg.cn/038a37cba1934496b06f5f9cffb6d338.png)