一.极坐标转换为普通坐标系

参考：极坐标方程与直角坐标方程的互化 - 知乎 (zhihu.com)

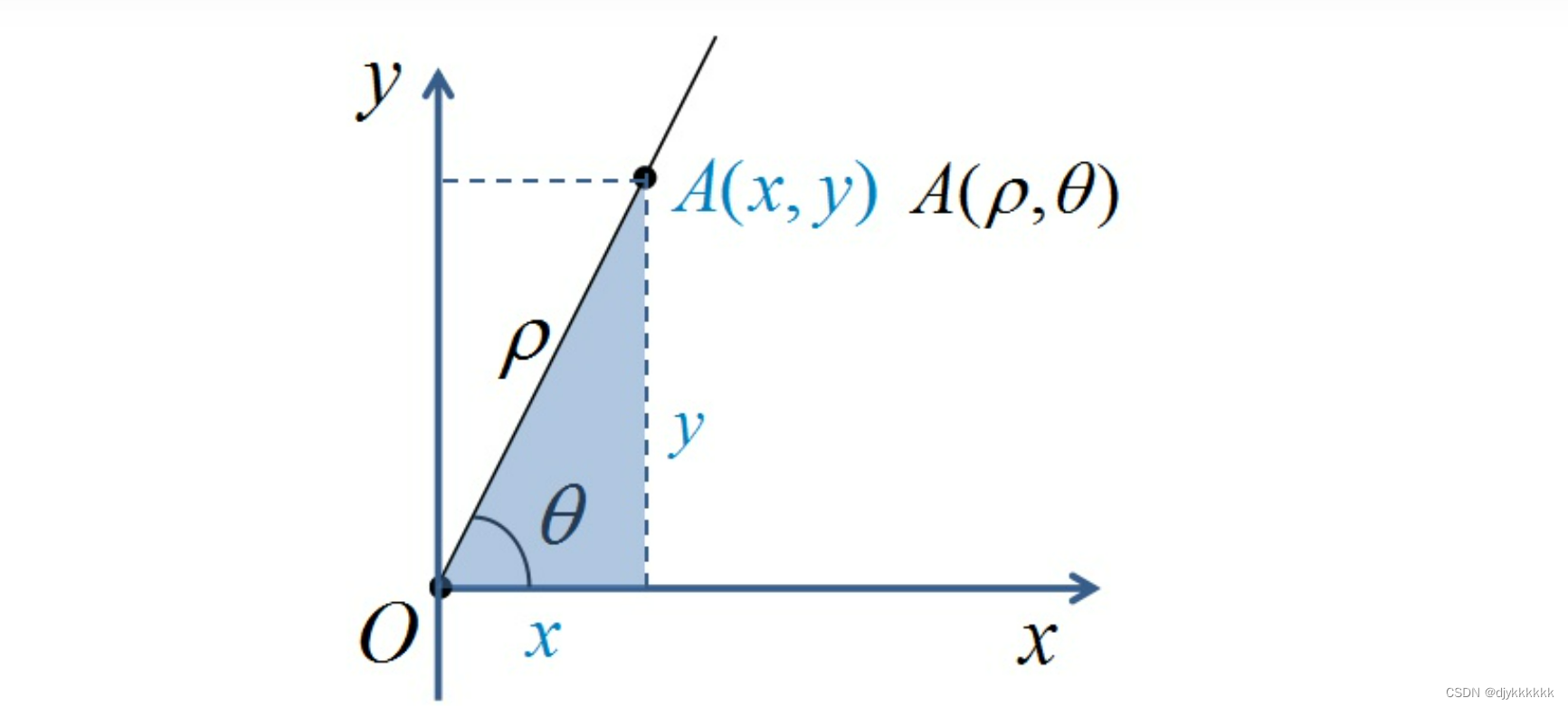
公式：（无需考虑象限引起的正负问题）

 

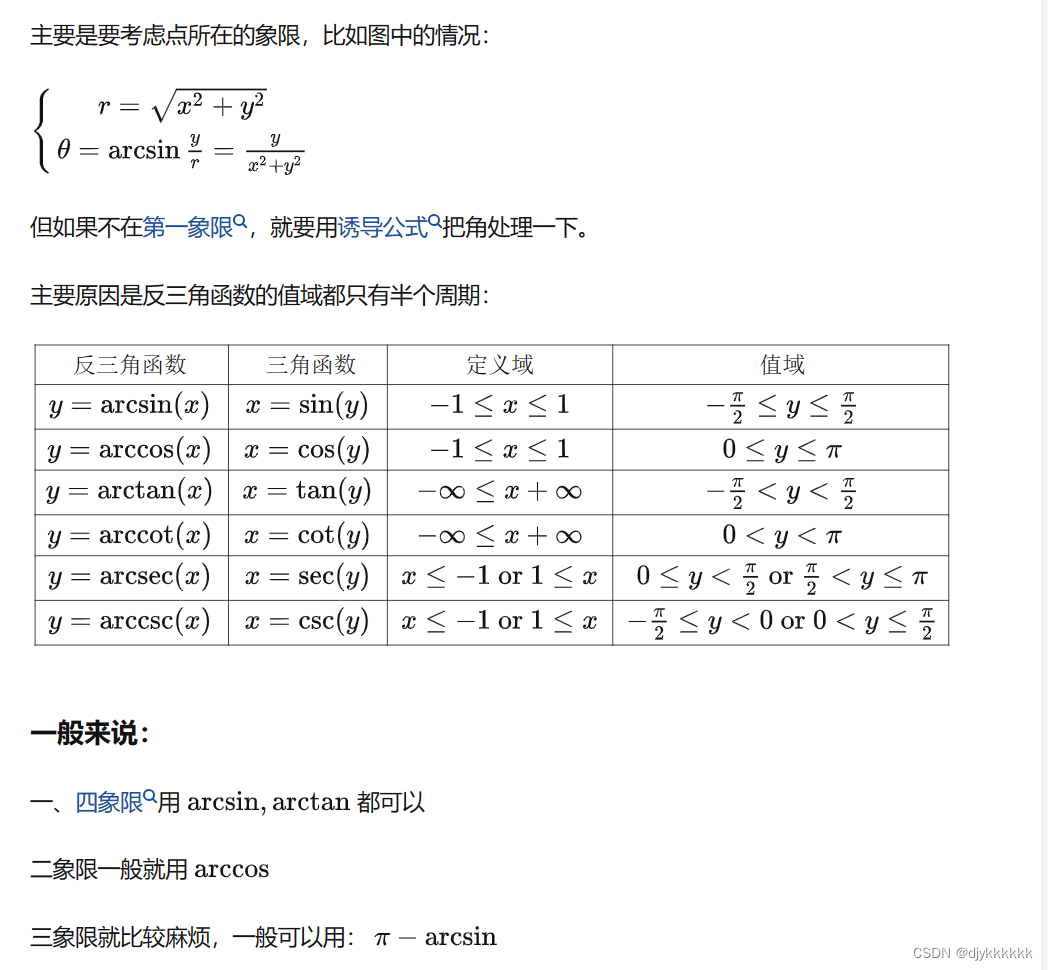
普通坐标系转换为极坐标系

参考： 极坐标怎么与直角坐标系相互转化？ - 知乎 (zhihu.com)

 

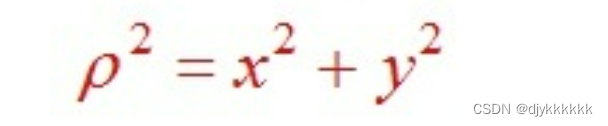
二.二维平面坐标系转换

二维坐标系的转换 - 漠刀凡尘 - 博客园 (cnblogs.com)

1.旋转变换

假设已知基坐标系XOY中的一点P（x，y），坐标原点为O，绕点O旋转θ，可以求得点P在新坐标系X'OY'中坐标值（x'，y'）,如下图所示：

 

求解x'和y'的关键是坚持用已知的边做斜边来求解，结合上图利用三角函数可以求得：

x'=x·cos(θ)+y·sin(θ)

y'=y·cos(θ)-x·sin(θ)

那么点P在X'OY'中的坐标值为（x',y'）。

同理如果知道P点在坐标系X'OY'中的坐标（x',y'）,可以求得点P在基坐标系XOY中的坐标值：

x=x'·cos(-θ)+y'·sin(-θ)

y=y'·cos(-θ)-x'·sin(-θ)

通过上述两个算式可以知道：已知一个点P在一个坐标系中的坐标值(x,y)，那么把坐标系绕坐标原点旋转θ以后，点P在新坐标系中的坐标值x'和y'分别为：

x'=x·cos(θ)+y·sin(θ)

y'=y·cos(θ)-x·sin(θ)

绕坐标原点逆时针旋转θ，上式θ值为正，顺时针旋转θ，上式θ值为负。

2.平移变换

已知基坐标系XOY，把坐标系平移(a,b)得到一个新的坐标系X'O'Y'，如果基坐标系中一点P(x,y)，跟随坐标系一起平移，那么此时P点在基坐标系XOY中的坐标为(x+a,y+b)。

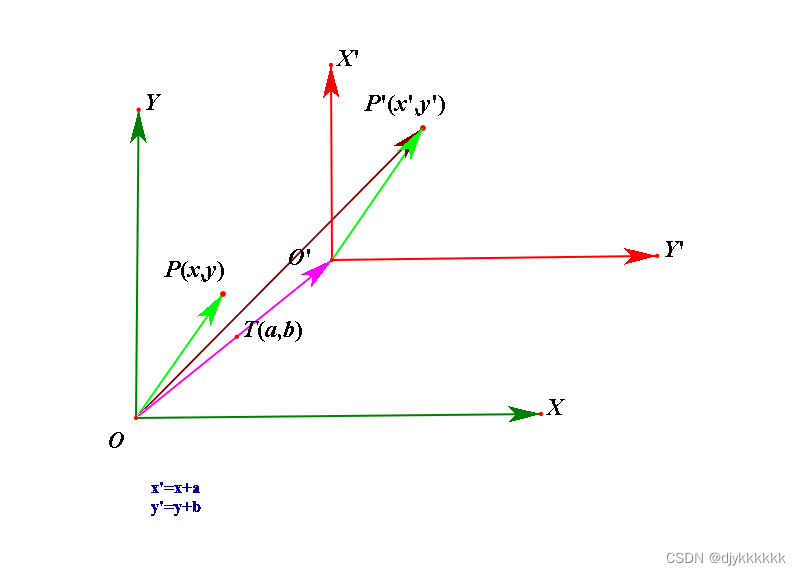
根据向量加法可以求得：

OP=OO'+O'P'=T+O'P'

所以向量OP'的坐标为(x+a,y+b)。

3.旋转平移变换

旋转平移变换是以上两种情况的叠加，已知旋转平移后的坐标系X'O'Y'中的一点P'(x',y')，求P'在基坐标系中的坐标值：

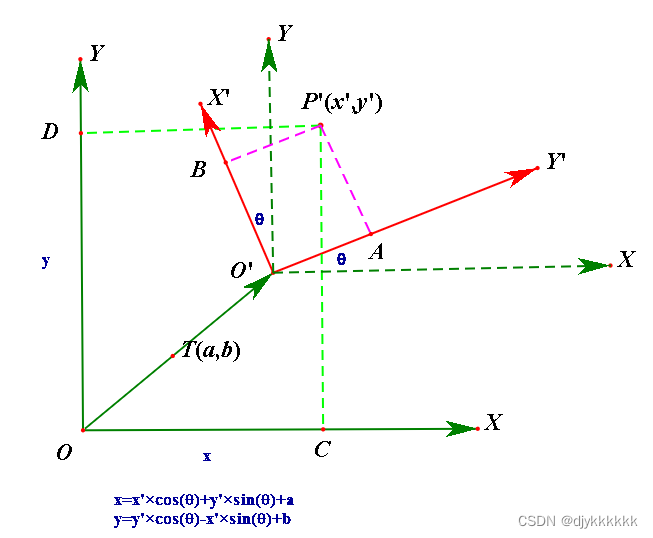
方法一：矩阵转换

可以先求出P'在坐标系XO'Y中的坐标值，X'O'Y'顺时针旋转θ（此时θ应取负值）可以变换为坐标系XO'Y，然后坐标系XO'Y经过平移(-a,-b)可以变换为坐标系XOY，至此可以求出坐标系X'O'Y'中的一点P'(x',y')在基坐标系XOY中的坐标值x，y分别为：

x=x'·cos(θ)+y'·sin(θ)+a
y=y'·cos(θ)-x'·sin(θ)+b

 方法二：

根据角度直接换算？？？