对于电路布线问题，想必学过动态规划的大家都很清除。今天就来讲解一下这个动态规划经典题目。

问题描述

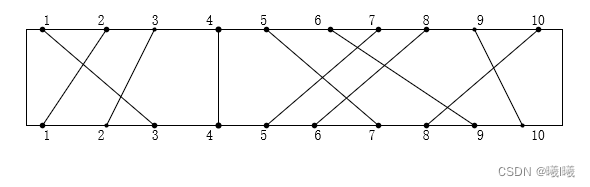
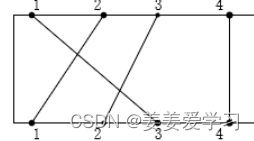
在一块电路板的上、下2端分别有n个接线柱。根据电路设计，要求用导 线(i,π(i))将上端接线柱与下端接线柱相连，如图所示。其中π(i)是 {1,2,…,n}的一个排列。导线(i,π(i))称为该电路板上的第i条连线。对于任 何1≤i<j≤n，第i条连线和第j条连线相交的充分且必要的条件是π(i)>π(j)。 电路布线问题要确定将哪些连线安排在第一层上，使得该层上有尽可能 多的连线。换句话说，该问题要求确定导线集Nets={(i,π(i)),1≤i≤n}的最 大不相交子集。

输入

两行输入
第一行是一排接线柱的个数
第二行是上接线柱对应的下接线柱位置，即下文的p(i)
对于上图输入就是
10
3 1 2 4 7 9 5 6 10 8

分析

那么什么是最大不相交子集呢。咱们来一个一个字 的 扣含义。
首先最大就是字面意思最大的，最多的。
其次不相交也是字面意思，就是单纯的两条线不能有交点。
最后子集的定义是如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集（通俗点说就是在给出的导线集合里面，挑选几条导线，这挑选的导线组成的集合就是子集）。
那么组合起来说的就是，在现有的线中挑选数量最多的导线且它们还不相交

我们发现这个题，好像不能从考虑最后一个步骤来推导了，我们好像还真不太好找出最后一个问题是什么。那么我们就换一种思路，回想以前的动态规划好像都是在数组中记录数值，供以后使用的而且都是一行一行的计算子问题。那我们先定义一个数组，考虑到有上下两排线，那就定义二维数组吧.。
设dp[i][j]表示前i个上接线柱和前j个下接线柱组成的问题的最优解包含的导线的数量(即前i个上接线柱和前j个下接线柱组成的集合的最大不相交子集中包含的导线数)

为了方便说明再来定义一些规则：
上接线柱集合（1，2，3，4…n）
下接线柱集合（p(1),p(2),p(3),p(4)…p(n)）
p(n)代表上层接线柱n对应的下层接线柱的编号。例如下图中上接线柱1，p(1)就是3

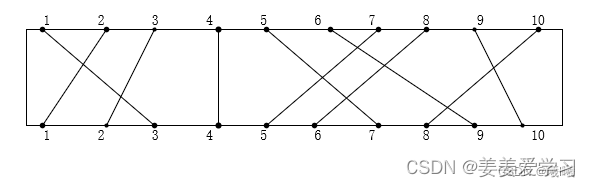
接下来以上图为例先从第一行来看，来找一下规律触发一下灵感
(第1步) i=1，j=1

(第2步) i=1，j=2

(第3步) i=1，j=3

唉突然发现此时，增加了一个，那就来想一想是什么原因让他增加的呢。我们发现当j>=p(1)时他就增加了，接下来继续看。
(第4步) i=1，j=3

然后类似的一直到 j==10 的时候
… …

(第10步) i=1，j=10

发现第一行除了j==3的时候增加了一个，其他的j>=p(1)的情况并没有增加为什么会这样呢？思考一下。因为我们的i是等于1的所以我们的dp[1][j]他最多只有一条线，我们上接线柱只包含了一个，所以他只能是小于等于一的数

这就给我们一个灵感我们可以根据i,p(i)的关系进行动态规划列出可能的情况加以分析

1.考虑当 i =1的时候
（1）j<p(i):肯定是零
（2）j>=p(i):他也肯定是一，因为这时最优解里面是空的，不用考虑香蕉🍌 （相交）的情况
2.考虑当 i>1时
（1）j<p(i):这时肯定还是不能包含这一条导线的，因为这一条导线的下接线柱没有被包含前 j 个里面。
那么这时他就相当于dp[i-1][j]。 为什么这么说呢？因为在j<p(i)时这一条导线是不可能被包含在我们的最优解里面的，所以就相当与这一条导线（i 导线）对于我们的当前的解是没有任何作用的。他就相当于是前 i -1个上接线柱和前 j 个下接线柱构成的问题的最优解。
也许此时聪明好学的你会问那为什么不是dp[i-1][j-1]呢？（即为什么不是前 i -1个上接线柱和前 j -1 个下接线柱构成的问题的最优解呢？。）
此时我们直接举一个一针见血的例子，如果i-1的下接线柱是 j 呢？dp[i-1][j-1]是不是就把第i-1条导线给漏掉了。
（2）j>=p(i): 这时候就说明我们可以包含这个导线，注意我说的是可以包含而不是一定包含。那么包含的条件是什么呢？想必你肯定已经知道了，就是当这条导线与最优解里面的导线都不香蕉🍌的时候 且 包含这个导线的最优解的个数比不包含这条导线的个数要大的时候才会包含 （dp[i][j]=Math.max(dp[i-1][p[i]-1]+1,dp[i-1][j])） 。而相交的时候就不可以包含了（dp[i][j]=dp[i-1][j]）。

最优子结构

1.对与i<1的时候肯定是满足的，因为他的子问题不就是空的集合吗。
2.对于i>1的时候
（1）j<p(i) 它的最优解所包含的导线个数是是子问题的最优解dp[i-1][j]。假设子问题的最优解不是dp[i-1][j]而是R那么R>dp[i-1][j]所以原问题的最优解应该是R，这就矛盾了。
（2）j>=p(i) 的时候他的子问题是选择这一条导线（dp[i-1][p[i]-1]+1）或则不选这一条导线（dp[i][j]=dp[i-1][j]）这两个中的最大值。对于不选择和上面的证明是一样的。
这里证明一下选择的情况：
在证明之前先了解一下子问题为什么是这个集合（前i-1个上接线柱，前p[i]-1个下接线柱）而不是其他的集合（例如前i-1个上接线柱，前j个下接线柱）。
我们既然选择了这一个导线就说明这个导线是不会与最优解里面的导线相交的。dp[i-1][p[i]-1]是前i-1个上接线柱，前p[i]-1个下接线柱 组成的解。我们的这一条导线对应的接线柱是i和p[i]。i>i-1且p[i]>p[i]-1所以他是这个集合中的最后一条线。就好比上图中的前4条导线，4是最后一条所以他肯定不
会与前三条相交的。

差不多理解了，就来证明最优子结构：
如果dp[i-1][p[i]-1]不是子问题的最优，最优的是R那么R+1>dp[i-1][p[i]-1]+1,所以由子问题构成的原问题的最优解应该是R+1而不是dp[i-1][p[i]-1]

代码

import java.util.Scanner;public class AD {public static void MSN(int n,int[] p,int[][] dp){for(int i=1;i<=n;i++){for (int j=1;j<=n;j++){if(i<=1){if(j<p[i]){dp[i][j]=dp[i-1][j];}else {dp[i][j]=1;}}else {if(j<p[i]){dp[i][j]=dp[i-1][j];}else {dp[i][j]=Math.max(dp[i-1][p[i]-1]+1,dp[i-1][j]);}}}}
}public static void main(String[] args) {Scanner scanner=new Scanner(System.in);int n=scanner.nextInt();int[] p=new int[n+1];p[0]=0;for(int i=1;i<=n;i++){p[i]=scanner.nextInt();}int[][] dp=new int[n+1][n+1];//        System.out.println(dp[n][n]);MSN(n,p,dp);System.out.println(dp[n][n]);}
}