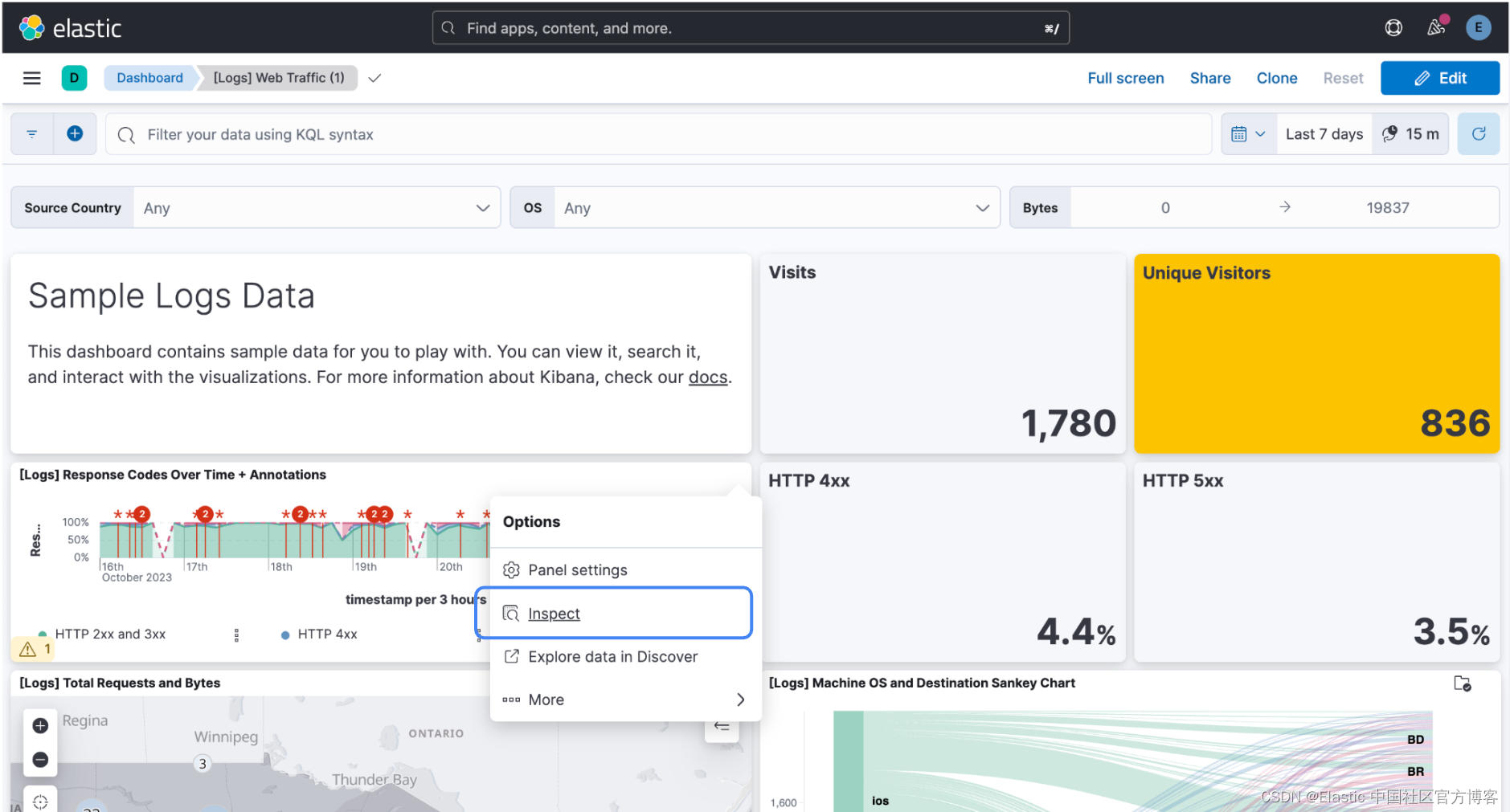
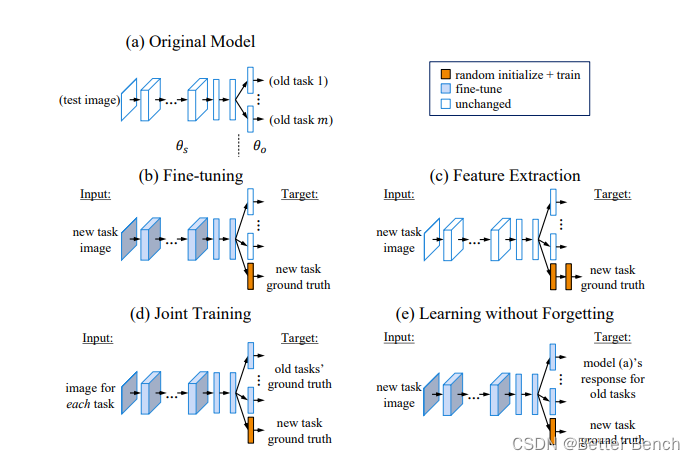
【力扣题】题目描述：

【Python3】代码：

1、解题思路：将整数转为字符串，遍历字符串中的数字，求和。

知识点：str(...)：转为字符串。为了遍历每个数字。

               int(...)：转为整数。为了数字求和。

               sum(...)：求和。

class Solution:def addDigits(self, num: int) -> int:while num >= 10:num = sum(int(x) for x in str(num))return num

2、解题思路：从右到左依次获取低位的数字，求和。

class Solution:def addDigits(self, num: int) -> int:while num >= 10:            # ① 若不是一位数即>=10，各位数相加，若相加后的值仍不是一位数，继续将值的各位数相加res = 0while num:res += num % 10     # 除法取余数，获取低位数字，求和num //= 10          # 除法取整数num = res               # ① return num

3、解题思路：数学。

同余原理：

一个正整数m，两个整数a和b，若(a-b)能被m整除（即(a-b)/m是整数），则a和b对模m同余，记作a≡b(mod m)。

简单理解：两个整数除以同一个正整数，余数相同，则两整数同余。

例如：整数11和1，模10。11%10=1，1%10=1，则11和1同余。或者 (11-1)/10=1(整数)，则11和1同余。

数根：又称数字根，每个正整数都有一个数根。

正整数，各位数相加，若值大于10，再各位数相加，最终得到一位数，即数根。

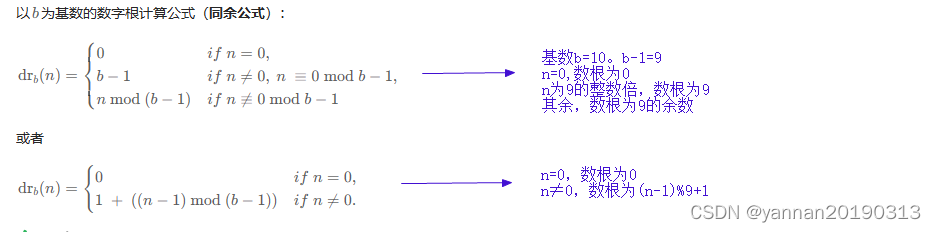
注解：n%10 结果为0-9，但10的整数倍的数根不符合。例如：10%10=0，但10的数根为1，不符合。

           n%9+1 结果为1-9，但9的整数倍的数根不符合。例如：9%9+1=1，但9的数根为9，不符合。 

          (n-1)%9+1 结果为1-9，符合，但仅限于大于0的整数。若为0，(0-1)%9+1=9，但0的数根为0。因此，n=0，结果为0；n>0，结果(n-1)%9+1。

class Solution:def addDigits(self, num: int) -> int:return (num - 1) % 9 + 1 if num else 0# 或者if num == 0: return 0if num % 9 == 0: return 9return num % 9