问题描述
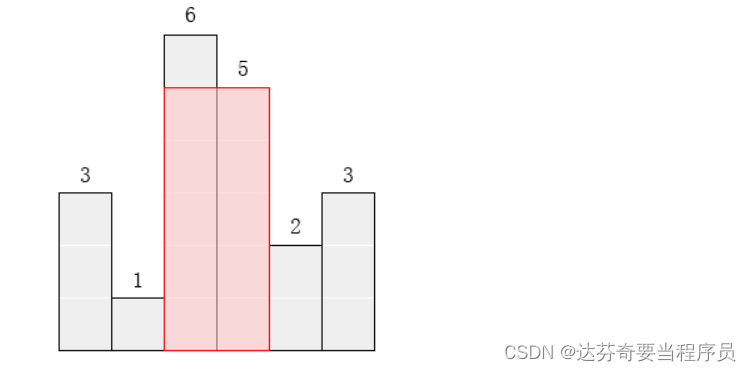
在横轴上放了n个相邻的矩形,每个矩形的宽度是1,而第i(1 ≤ i ≤ n)个矩形的高度是hi。这n个矩形构成了一个直方图。例如,下图中六个矩形的高度就分别是3, 1, 6, 5, 2, 3。

请找出能放在给定直方图里面积最大的矩形,它的边要与坐标轴平行。对于上面给出的例子,最大矩形如下图所示的阴影部分,面积是10。
输入格式
第一行包含一个整数n,即矩形的数量(1 ≤ n ≤ 1000)。
第二行包含n 个整数h1, h2, … , hn,相邻的数之间由空格分隔。(1 ≤ hi ≤ 10000)。hi是第i个矩形的高度。
输出格式
输出一行,包含一个整数,即给定直方图内的最大矩形的面积。
样例输入
6
3 1 6 5 2 3
样例输出
10
解答
思路:
//从第一列开始,以第一列为底*最小高度,依次多加一列*最小高度,循环记录最大值。
//再从第二列开始,以第二列为底*最小高度,依次多加一列*最小高度,循环记录最大值。
//依次类推到最后一列;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner=new Scanner(System.in);//记录行数int n=scanner.nextInt();//以数组记录行高int[] arr=new int[n];//记录从每列开始包含最大矩形面积int[] arrResult=new int[n];//输入行高for(int i=0;i<n;i++) {arr[i]=scanner.nextInt();}//从第一列开始,以第一列为底*最小高度,依次多加一列*最小高度,循环记录最大值。//再从第二列开始,以第二列为底*最小高度,依次多加一列*最小高度,循环记录最大值。//依次类推到最后一列;for(int i=0;i<n;i++) {int maxnum=0;int shortest=arr[i];for(int j=i,k=i;j<n;j++) {if(arr[j]<shortest) {shortest=arr[j];}if(shortest*(j+1-k)>maxnum) {maxnum=shortest*(j+1-k);}}arrResult[i]=maxnum;}//找出最大矩阵面积int maxValue=0;for(int i=0;i<n;i++) {if(maxValue<arrResult[i]) {maxValue=arrResult[i];}}System.out.println(maxValue);}
}