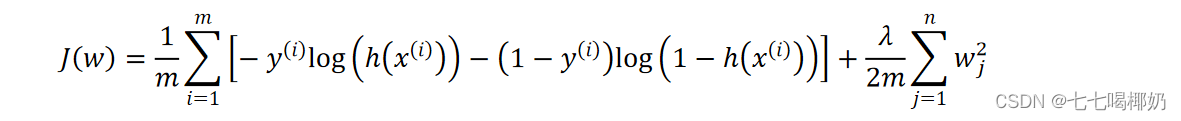目录

一、分类问题

监督学习的最主要类型

二分类

多分类

二、Sigmoid函数

三、逻辑回归求解

 代价函数推导过程（极大似然估计）：

交叉熵损失函数 

逻辑回归的代价函数

代价函数最小化——梯度下降： ​编辑

 正则化

四、逻辑回归代码实现

Sigmoid 函数

代价函数

​编辑 正则化

---

一、分类问题

监督学习的最主要类型

分类（Classification）：

• 身高1.85m，体重100kg的男人穿什么尺码的T恤？
• 根据肿瘤的体积、患者的年龄来判断良性或恶性？
• 根据用户的年龄、职业、存款数量来判断信用卡是否会违约？

 输入变量可以是离散的，也可以是连续的。

二分类

们先从用蓝色圆形数据定义为类型1，其余数据为类型2； 只需要分类1次 步骤：①->②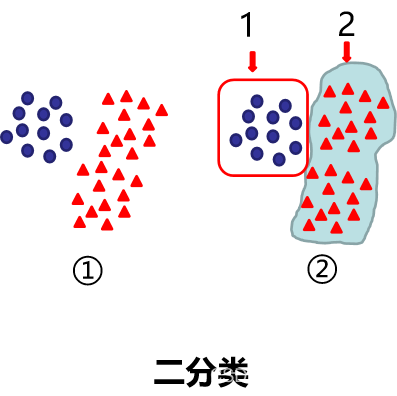

多分类

我们先定义其中一类为类型1（正类），其余数据为负类（rest）； 接下来去掉类型1数据，剩余部分再次进行二分类，分成类型2和负类；如果有n类，那就需要分类n-1次 步骤：①->②->③->……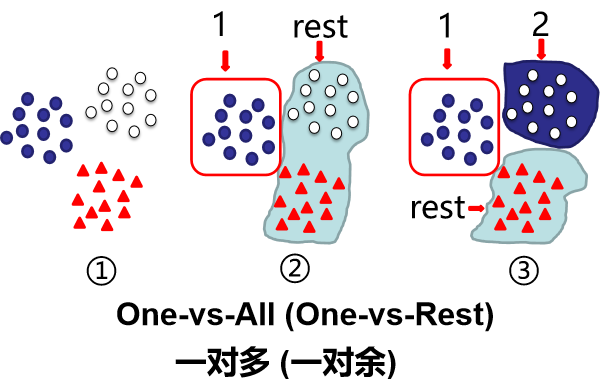

二、Sigmoid函数

σ(z)代表一个常用的逻辑函数（logistic function）为S形函数（Sigmoid function）

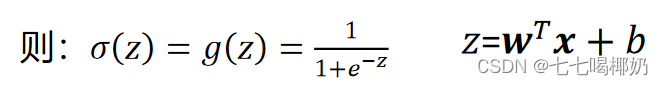
合起来，我们得到逻辑回归模型的假设函数：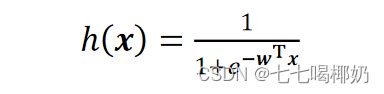 

当σ(z)大于等于0.5时，预测 y =1

当σ(z)小于0.5时，预测 y =0 

三、逻辑回归求解

逻辑回归模型的假设函数：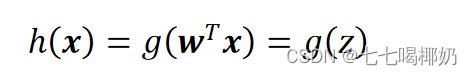

逻辑函数（logistic function)公式为：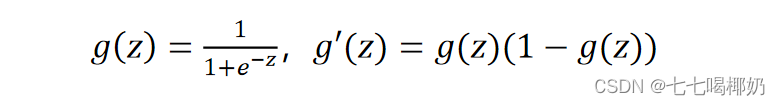

二分类相当于一个概率模型：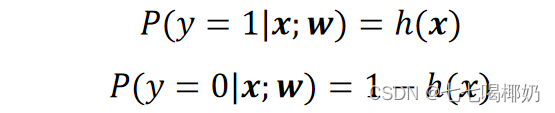 

合起来：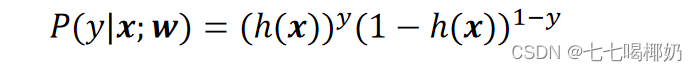

 代价函数推导过程（极大似然估计）：

似然函数为：

似然函数两边取对数，则连乘号变成了连加号：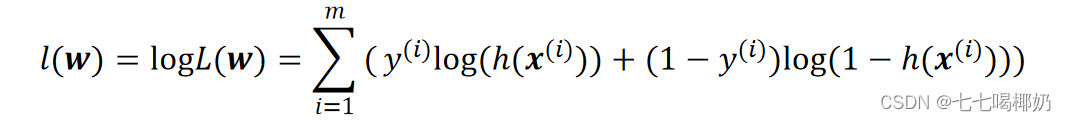

代价函数为：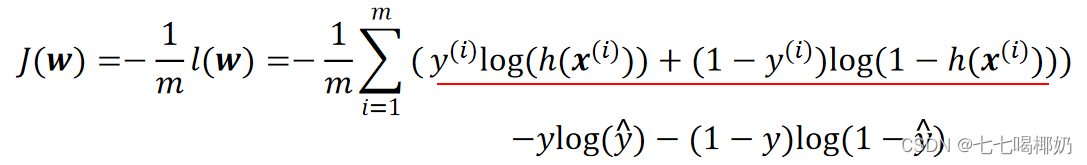

交叉熵损失函数 

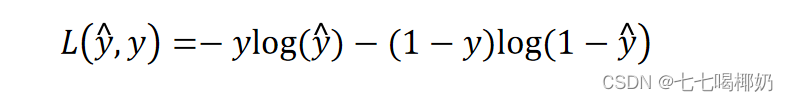
代价函数就是对m个样本的损失函数求和然后除以m:

逻辑回归的代价函数

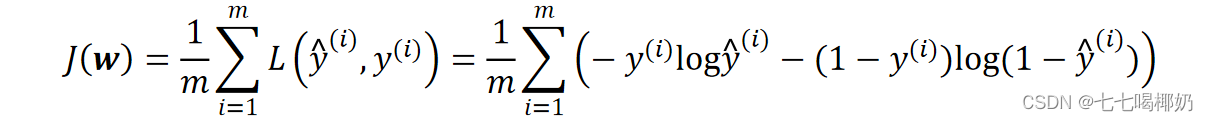
代价函数最小化——梯度下降： 

 正则化

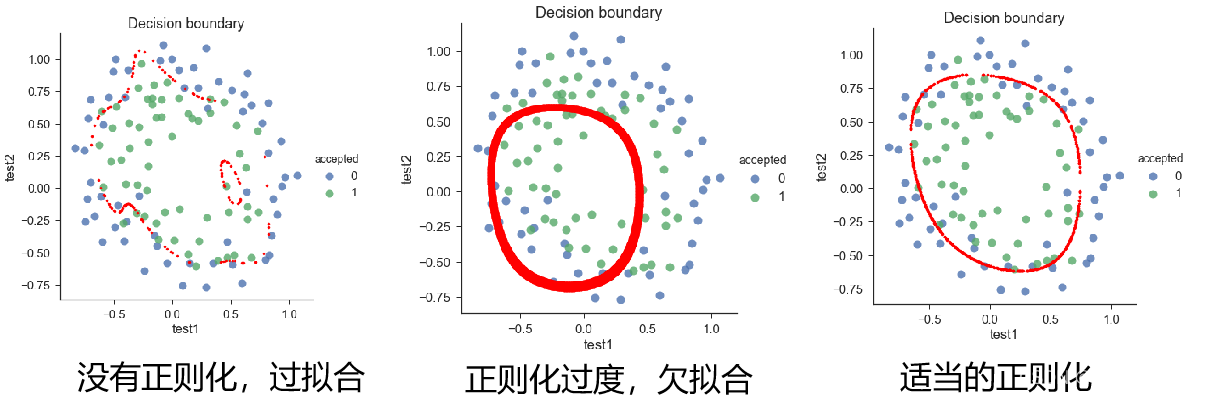
正则化：目的是为了防止过拟合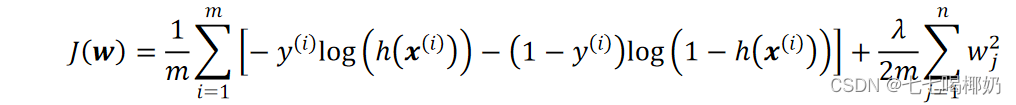

当 λ 的值开始上升时，降低了方差。

四、逻辑回归代码实现

Sigmoid 函数

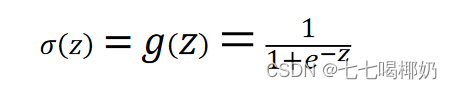
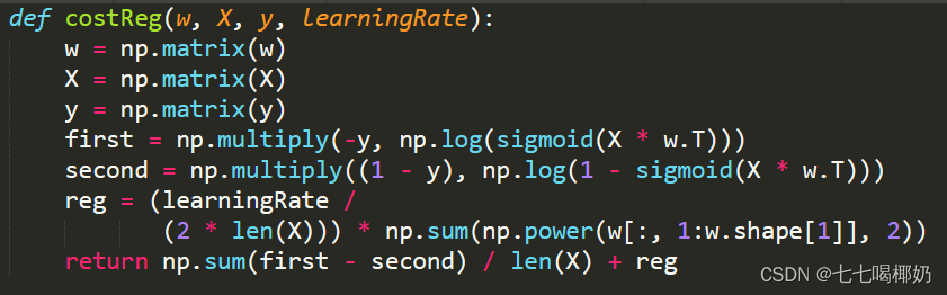
代价函数

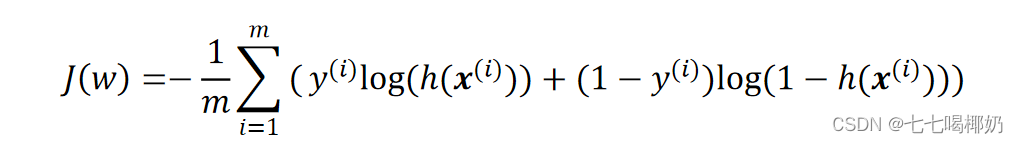
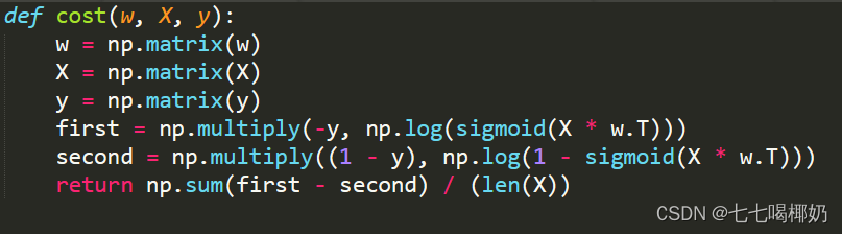 正则化