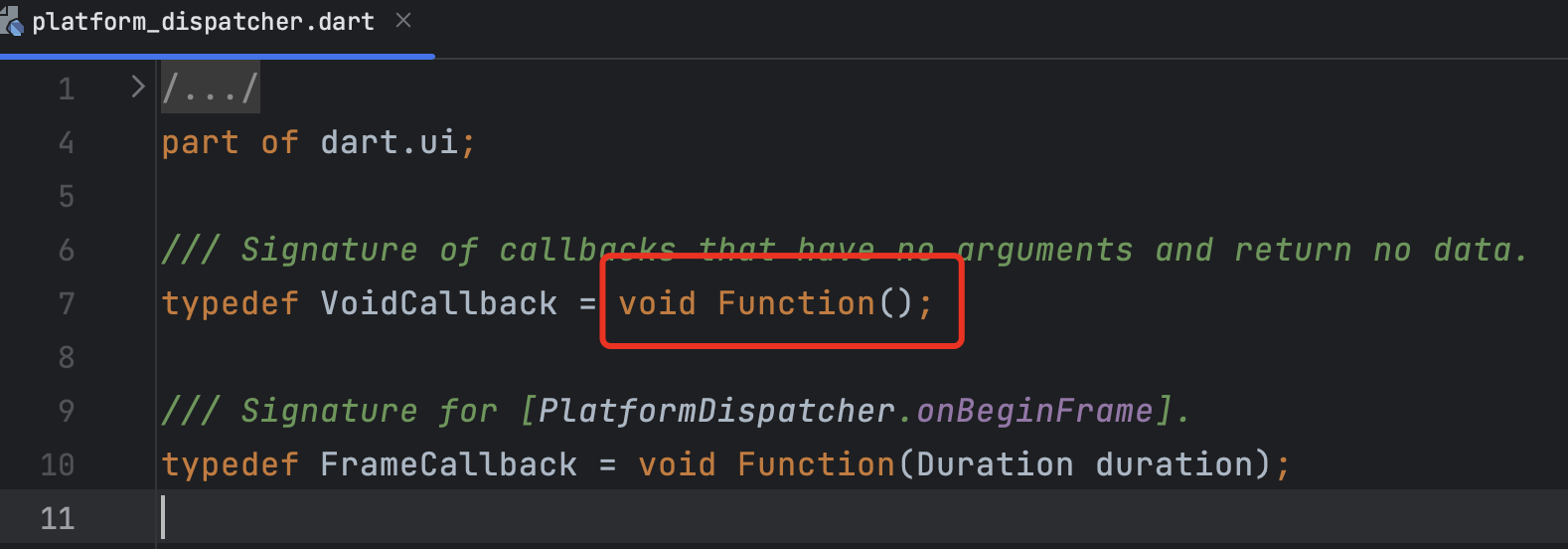
题目

思路来源
P9388 [THUPC 2023 决赛] 先人类的人类选别 - 违规用户名FkZyA0!2 的博客 - 洛谷博客
题解
这个题是2023ccpc深圳热身赛的题目,也是thupc2023决赛的题目,
学弟问了一下,于是就乱搞了一下,搞了很久才a,赛后一看题解直呼自己sb
不过主席树和权值线段树两棵树叠加在一起的操作也确实很少见,也记录一下吧
正解
观察到操作序列一定时,操作顺序对答案并没有影响。
将询问[l,r]拆成前缀和作差,也就是[1,r]减去[1,l-1]
在时刻q时,对于一个前缀区间[1,x],
操作的本质,相当于把[1,x]原来的数和[1,q]询问中出现的数放在一起,
取最小的q个值丢给后面
想求[1,x]的和,也就是求得总和和最小的q个值的和即可,无需关注具体位置
所以可以将原序列中的数维护在一棵主席树上,
将询问中出现的数,在线维护在一棵权值线段树上,
由于主席树sum可以作差的性质,那么两棵树叠在一起也是可以作和的
查询的时候,按照值域,在两棵树叠在一起的树上一起跑即可
乱搞AC(五棵线段树)

这个操作是在维护一个冒泡非严格降序序列,
考虑主要维护三棵树,一棵A线段树是原始序列中不在冒泡序列里的,
另两棵,B线段树维护冒泡序列的位置,C线段树维护权值线段树当前有哪些值
于是就需要求,每个值是在哪个时刻被扔进冒泡序列里的,
对于一个数x,记其左侧<=x的数的个数为y,那么其rank为y+1
那么只有当询问中出现第y+1个>x的数时,
数x才会被拔高,也就是会被扔进冒泡序列里,
记第i个数被拔高的时刻是dfn[i],考虑怎么求
一开始是整体二分两个log求的dfn,
也就是按时间序把n个位置时间序的m个时间节点放一起二分
结果两个logT了,
想了一会,改成了现在这个1log动态全局删点的,
先将n个位置按值从小到大排增序,如果值相同,从左到右排增序,
线段树上每个位置的初始值是其左侧小于等于这个数的数的个数,
询问中每出现一个数x,就对小于x的位置区间减1,
当有位置被减到0时,说明在本轮被拔高,
加入对应时刻的dfn,动态删点给删掉即可
所以需要维护区间最小值,动态删点时,给单点置为INF
那么,除了图中的ABC三棵树外,
一棵线段树用于求每个数的rank,另一棵线段树用于区间减1和动态删点
所以最后是五棵线段树,降成了O(nlogn),
以为3s时限比较稳,但是常数巨大,开O2跑了2.99s,属实没绷住
代码1(正解)
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define int long long
#define maxn 500005
int n,m;
int a[maxn],suf[maxn],root[maxn],rota,cnt;
struct node {int ls,rs,sum,siz;
} f[maxn*30];
int Update(int l,int r,int pre,int head) {int rt=++cnt;f[rt]=f[pre];f[rt].siz++;f[rt].sum+=head;if (l==r) return rt;int mid=l+r>>1;if (head<=mid) f[rt].ls=Update(l,mid,f[rt].ls,head);else f[rt].rs=Update(mid+1,r,f[rt].rs,head);return rt;
}
void Update2(int l,int r,int &rt,int head) {if (!rt) rt=++cnt;f[rt].siz++,f[rt].sum+=head;if (l==r) return ;int mid=l+r>>1;if (head<=mid) Update2(l,mid,f[rt].ls,head);else Update2(mid+1,r,f[rt].rs,head);
}
int Query(int l,int r,int rt1,int rt2,int k) {if (l==r) return k*l;int mid=l+r>>1,siz=f[f[rt1].ls].siz+f[f[rt2].ls].siz;if (siz>=k) return Query(l,mid,f[rt1].ls,f[rt2].ls,k);else return f[f[rt1].ls].sum+f[f[rt2].ls].sum+Query(mid+1,r,f[rt1].rs,f[rt2].rs,k-siz);
}
signed main(void) {int i,x,l,r,sum=0;scll(n);scll(m);for (i=1; i<=n; i++) scll(a[i]),suf[i]=suf[i-1]+a[i];for (i=1; i<=n; i++) {root[i]=Update(1,n,root[i-1],a[i]);}for (i=1; i<=m; i++) {scll(x);scll(l);scll(r);sum+=x;Update2(1,n,rota,x);int tmp1=suf[l-1]+sum-Query(1,n,root[l-1],rota,i);int tmp2=suf[r]+sum-Query(1,n,root[r],rota,i);printf("%lld\n",tmp2-tmp1);}return 0;
}代码2(乱搞AC)
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=5e5+10,INF=0x3f3f3f3f;
int n,m,id[N],a[N];
vector<int>dfn[N];
P b[N];
ll rk[N],ans;
struct qeury{int x,l,r;void rd(){sci(x),sci(l),sci(r);}
}e[N];
struct segtree{int n;struct node{int l,r;ll v,s;}e[N<<2];#define l(p) e[p].l#define r(p) e[p].r#define v(p) e[p].v#define s(p) e[p].svoid up(int p){v(p)=v(p<<1)+v(p<<1|1);s(p)=s(p<<1)+s(p<<1|1);}void bld(int p,int l,int r){l(p)=l;r(p)=r;s(p)=v(p)=0;if(l==r){return;}int mid=l+r>>1;bld(p<<1,l,mid);bld(p<<1|1,mid+1,r);up(p);}void init(int _n){n=_n;bld(1,1,n);}void chg(int p,int x,int v){if(l(p)==r(p)){v(p)=v;return;}int mid=l(p)+r(p)>>1;chg(p<<1|(x>mid),x,v);up(p);}void add(int p,int x,int v){if(l(p)==r(p)){v(p)+=v;s(p)+=1ll*l(p)*v;return;}int mid=l(p)+r(p)>>1;add(p<<1|(x>mid),x,v);up(p);}ll cnt(int p,int ql,int qr){if(ql>qr)return 0;if(ql<=l(p)&&r(p)<=qr)return v(p);int mid=l(p)+r(p)>>1;ll res=0;if(ql<=mid)res+=cnt(p<<1,ql,qr);if(qr>mid)res+=cnt(p<<1|1,ql,qr);return res;}ll topK(int p,int k){if(k<=0)return 0;if(l(p)==r(p))return 1ll*k*l(p);if(v(p<<1|1)>=k)return topK(p<<1|1,k);return s(p<<1|1)+topK(p<<1,k-v(p<<1|1));}
}tr[4];
struct segtree2{int n;struct node{int l,r,v,c;}e[N<<2];#define l(p) e[p].l#define r(p) e[p].r#define v(p) e[p].v#define c(p) e[p].cvoid up(int p){v(p)=min(v(p<<1),v(p<<1|1));}void bld(int p,int l,int r){l(p)=l;r(p)=r;v(p)=INF;c(p)=0;if(l==r){return;}int mid=l+r>>1;bld(p<<1,l,mid);bld(p<<1|1,mid+1,r);up(p);}void psd(int p){if(c(p)){v(p<<1)+=c(p);c(p<<1)+=c(p);v(p<<1|1)+=c(p); c(p<<1|1)+=c(p);c(p)=0; }}void init(int _n){n=_n;bld(1,1,n);}void chg(int p,int x,int v){if(l(p)==r(p)){v(p)=v;return;}int mid=l(p)+r(p)>>1;psd(p);chg(p<<1|(x>mid),x,v);up(p);}void del(int p,int x){if(l(p)==r(p)){v(p)=INF;return;}int mid=l(p)+r(p)>>1;psd(p);del(p<<1|(x>mid),x);up(p);}void add(int p,int ql,int qr,int v){if(ql>qr)return;if(ql<=l(p)&&r(p)<=qr){v(p)+=v;c(p)+=v;return;}psd(p);int mid=l(p)+r(p)>>1;if(ql<=mid)add(p<<1,ql,qr,v);if(qr>mid)add(p<<1|1,ql,qr,v);up(p);}int fmn(int p){//printf("p:%d vp:%d vlp:%d vrp:%d\n",p,v(p),v(p<<1),v(p<<1|1));if(v(p)>0)return 0;if(l(p)==r(p))return l(p);int mid=l(p)+r(p)>>1;psd(p);if(v(p<<1)<=0)return fmn(p<<1);else return fmn(p<<1|1);}
}seg;
int main(){sci(n),sci(m);rep(i,0,3)tr[i].init(n);seg.init(n);rep(i,1,n){sci(a[i]);tr[0].chg(1,i,a[i]);tr[3].add(1,a[i],1);rk[i]=tr[3].cnt(1,1,a[i]);//seg.chg(1,i,rk[i]);b[i]=P(a[i],i);//printf("i:%d rk:%d\n",i,rk[i]);}sort(b+1,b+n+1);rep(i,1,n){seg.chg(1,i,rk[b[i].se]);//printf("i:%d bi.se:%d rk:%d\n",i,b[i].se,rk[b[i].se]);}b[n+1]=P(n+1,0);rep(i,1,m){e[i].rd();int p=lower_bound(b+1,b+n+2,P(e[i].x,0))-b;p--;//printf("i:%d p:%d\n",i,p);seg.add(1,1,p,-1);int p2;while((p2=seg.fmn(1))>0){//printf("i:%d p2:%d\n",i,p2);dfn[i].pb(b[p2].se);seg.del(1,p2);}}rep(i,1,m){int x=e[i].x,l=e[i].l,r=e[i].r;for(auto &p:dfn[i]){//printf("i:%d p:%d\n",i,p);tr[0].add(1,p,-a[p]);tr[1].add(1,p,1);tr[2].add(1,a[p],1);}tr[2].add(1,x,1);ans=tr[0].cnt(1,l,r);int k1=tr[1].cnt(1,1,l-1);int k2=tr[1].cnt(1,1,r);ans+=tr[2].topK(1,k2)-tr[2].topK(1,k1);printf("%lld\n",ans);}return 0;
}