300.最长递增子序列
思路
首先通过本题大家要明确什么是子序列,“子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序”。
本题也是代码随想录中子序列问题的第一题,如果没接触过这种题目的话,本题还是很难的,甚至想暴力去搜索也不知道怎么搜。 子序列问题是动态规划解决的经典问题,当前下标i的递增子序列长度,其实和i之前的下表j的子序列长度有关系,那又是什么样的关系呢。
接下来,我们依然用动规五部曲来详细分析一波:
- dp[i]的定义
本题中,正确定义dp数组的含义十分重要。
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度
为什么一定表示 “以nums[i]结尾的最长递增子序” ,因为我们在 做 递增比较的时候,如果比较 nums[j] 和 nums[i] 的大小,那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾, 要不然这个比较就没有意义了,不是尾部元素的比较那么 如何算递增呢。
- 状态转移方程
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
注意这里不是要dp[i] 与 dp[j] + 1进行比较,而是我们要取dp[j] + 1的最大值。
- dp[i]的初始化
每一个i,对应的dp[i](即最长递增子序列)起始大小至少都是1.
- 确定遍历顺序
dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来,那么遍历i一定是从前向后遍历。
j其实就是遍历0到i-1,那么是从前到后,还是从后到前遍历都无所谓,只要吧 0 到 i-1 的元素都遍历了就行了。 所以默认习惯 从前向后遍历。
遍历i的循环在外层,遍历j则在内层,代码如下:
for (int i = 1; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);}if (dp[i] > result) result = dp[i]; // 取长的子序列
}
- 举例推导dp数组
输入:[0,1,0,3,2],dp数组的变化如下:
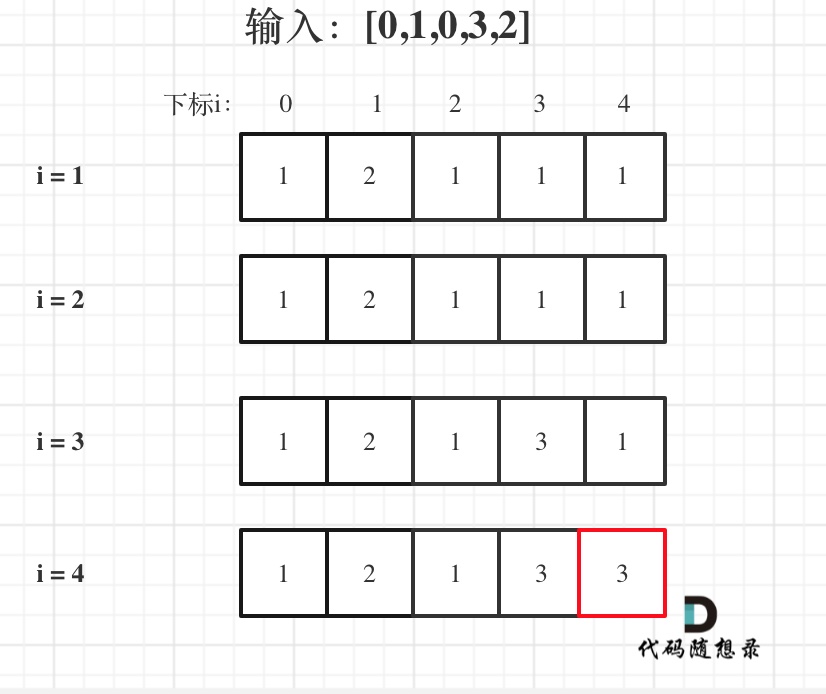
如果代码写出来,但一直AC不了,那么就把dp数组打印出来,看看对不对!
以上五部分析完毕,C++代码如下:
class Solution {public int lengthOfLIS(int[] nums) {int[] dp = new int[nums.length];Arrays.fill(dp,1);int result = 1;for (int i = 1; i < nums.length; i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]){dp[i] = Math.max(dp[i],dp[j]+1);}result = Math.max(result,dp[i]);// 取长的子序列}}return result;}
}- 时间复杂度: O(n^2)
- 空间复杂度: O(n)
#总结
本题最关键的是要想到dp[i]由哪些状态可以推出来,并取最大值,那么很自然就能想到递推公式:dp[i] = max(dp[i], dp[j] + 1);
674. 最长连续递增序列
思路
动态规划
动规五部曲分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i]:以下标i为结尾的连续递增的子序列长度为dp[i]。
注意这里的定义,一定是以下标i为结尾,并不是说一定以下标0为起始位置。
- 确定递推公式
如果 nums[i] > nums[i - 1],那么以 i 为结尾的连续递增的子序列长度 一定等于 以i - 1为结尾的连续递增的子序列长度 + 1 。
即:dp[i] = dp[i - 1] + 1;
注意这里就体现出和动态规划:300.最长递增子序列 (opens new window)的区别!
因为本题要求连续递增子序列,所以就只要比较nums[i]与nums[i - 1],而不用去比较nums[j]与nums[i] (j是在0到i之间遍历)。
既然不用j了,那么也不用两层for循环,本题一层for循环就行,比较nums[i] 和 nums[i - 1]。
这里大家要好好体会一下!
- dp数组如何初始化
以下标i为结尾的连续递增的子序列长度最少也应该是1,即就是nums[i]这一个元素。
所以dp[i]应该初始1;
- 确定遍历顺序
从递推公式上可以看出, dp[i + 1]依赖dp[i],所以一定是从前向后遍历。
本文在确定递推公式的时候也说明了为什么本题只需要一层for循环,代码如下:
for (int i = 1; i < nums.length; i++) {if (nums[i] > nums[i-1]){dp[i] = dp[i-1]+1;// 连续记录result = Math.max(dp[i],result);}
}- 举例推导dp数组
已输入nums = [1,3,5,4,7]为例,dp数组状态如下:
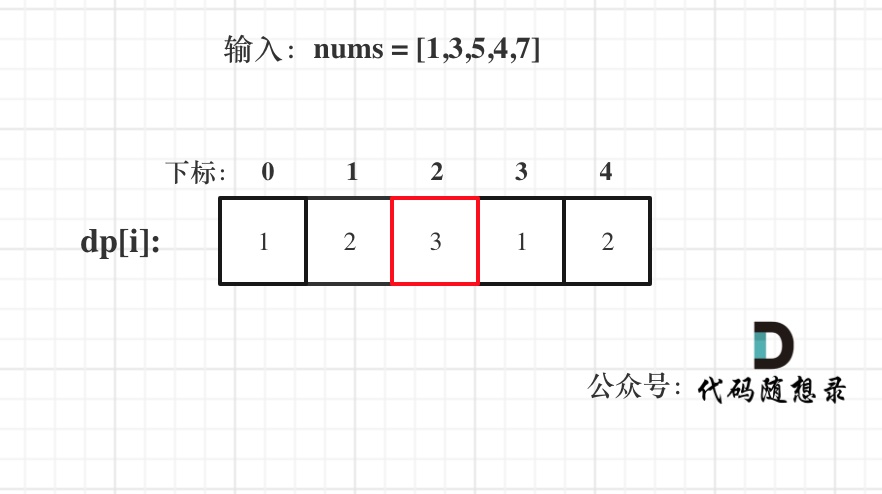
注意这里要取dp[i]里的最大值,所以dp[2]才是结果!
以上分析完毕,代码如下:
class Solution {public int findLengthOfLCIS(int[] nums) {int[] dp = new int[nums.length];Arrays.fill(dp,1);int result = 1;for (int i = 1; i < nums.length; i++) {if (nums[i] > nums[i-1]){dp[i] = dp[i-1]+1;// 连续记录result = Math.max(dp[i],result);}}return result;}
}- 时间复杂度:O(n)
- 空间复杂度:O(n)
718. 最长重复子数组
思路
注意题目中说的子数组,其实就是连续子序列。
要求两个数组中最长重复子数组,如果是暴力的解法 只需要先两层for循环确定两个数组起始位置,然后再来一个循环可以是for或者while,来从两个起始位置开始比较,取得重复子数组的长度。
本题其实是动规解决的经典题目,我们只要想到 用二维数组可以记录两个字符串的所有比较情况,这样就比较好推 递推公式了。 动规五部曲分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i][j] :以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]。 (特别注意: “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 )
此时细心的同学应该发现,那dp[0][0]是什么含义呢?总不能是以下标-1为结尾的A数组吧。
其实dp[i][j]的定义也就决定着,我们在遍历dp[i][j]的时候i 和 j都要从1开始。
那有同学问了,我就定义dp[i][j]为 以下标i为结尾的A,和以下标j 为结尾的B,最长重复子数组长度。不行么?
行倒是行! 但实现起来就麻烦一点,需要单独处理初始化部分,在本题解下面的拓展内容里,我给出了 第二种 dp数组的定义方式所对应的代码和讲解,大家比较一下就了解了。
- 确定递推公式
根据dp[i][j]的定义,dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来。
即当A[i - 1] 和B[j - 1]相等的时候,dp[i][j] = dp[i - 1][j - 1] + 1;
根据递推公式可以看出,遍历i 和 j 要从1开始!
- dp数组如何初始化
根据dp[i][j]的定义,dp[i][0] 和dp[0][j]其实都是没有意义的!
但dp[i][0] 和dp[0][j]要初始值,因为 为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;
所以dp[i][0] 和dp[0][j]初始化为0。
举个例子A[0]如果和B[0]相同的话,dp[1][1] = dp[0][0] + 1,只有dp[0][0]初始为0,正好符合递推公式逐步累加起来。
- 确定遍历顺序
外层for循环遍历A,内层for循环遍历B。
那又有同学问了,外层for循环遍历B,内层for循环遍历A。不行么?
也行,一样的,我这里就用外层for循环遍历A,内层for循环遍历B了。
同时题目要求长度最长的子数组的长度。所以在遍历的时候顺便把dp[i][j]的最大值记录下来。
代码如下:
for (int i = 1; i <= nums1.length; i++) {for (int j = 1; j <= nums2.length; j++) {if (nums1[i-1] == nums2[j-1]){dp[i][j] = dp[i-1][j-1]+1;result = Math.max(dp[i][j],result);}}
}- 举例推导dp数组
拿示例1中,A: [1,2,3,2,1],B: [3,2,1,4,7]为例,画一个dp数组的状态变化,如下:
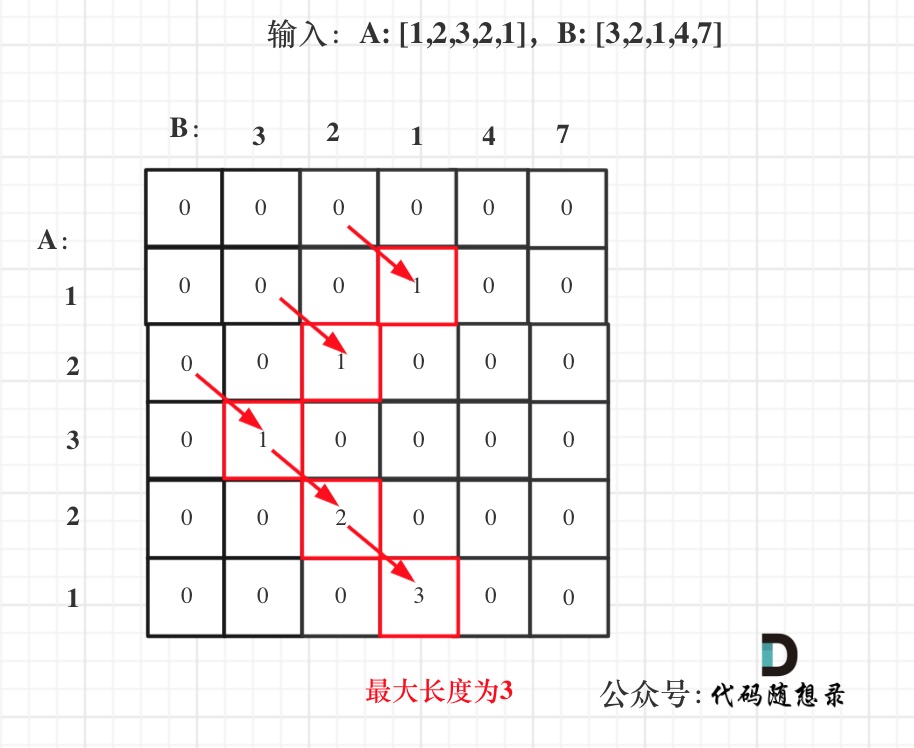
以上五部曲分析完毕,代码如下:
class Solution {public int findLength(int[] nums1, int[] nums2) {//确定dp数组 dp[i][j] :// 以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]。// (特别注意: “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 )int[][] dp = new int[nums1.length+1][nums2.length+1];//初始化dp数组及确定遍历顺序 dp[i][j] = dp[i - 1][j - 1] + 1;int result = 0;for (int i = 1; i <= nums1.length; i++) {for (int j = 1; j <= nums2.length; j++) {if (nums1[i-1] == nums2[j-1]){dp[i][j] = dp[i-1][j-1]+1;result = Math.max(dp[i][j],result);}}}return result;}
}- 时间复杂度:O(n × m),n 为A长度,m为B长度
- 空间复杂度:O(n × m)
最后一题的递推公式的内涵要跟着图来一步一步理解。但是还是很难理解,之后二刷得对动规上点心了




![[论文阅读] CLRerNet: Improving Confidence of Lane Detection with LaneIoU](https://img-blog.csdnimg.cn/914be7db17eb404491ad773e49a61a6f.png)