本系列文章将从下面不同角度解析线性代数的本质,本文是本系列第二篇
向量究竟是什么?
向量的线性组合,基与线性相关
矩阵与线性相关
矩阵乘法与复合线性变换
三维空间中的线性变换
行列式
逆矩阵,列空间,秩与零空间
克莱姆法则
非方阵
点积与对偶性
叉积
以线性变换眼光看叉积
基变换
特征向量与特征值
抽象向量空间
快速计算二阶矩阵特征值
张量,协变与逆变和秩
文章目录
- 矩阵乘法与复合线性变换
- 三维空间中的线性变换
- 行列式
矩阵乘法与复合线性变换
我们已经知道矩阵是一种线性变换,现在对基向量连续施加两种线性变换,例如,先旋转,再剪切,其实,这在整体上可以看作是一种新的变换,这个新的变换被称为前两种独立变换的“复合变换”。
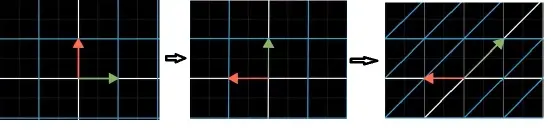
这个复合变换的矩阵可以通过追踪基向量的坐标得到,如上图所示,变换后的 i ⃗ \vec{i} i坐标 [ 1 1 ] \begin{bmatrix} 1\\ 1 \end{bmatrix} [11],变换后的 j ⃗ \vec{j} j坐标 [ − 1 0 ] \begin{bmatrix} -1\\ 0 \end{bmatrix} [−10],那么该复合变换矩阵就可以表示为: [ 1 − 1 1 0 ] \begin{bmatrix} 1 & -1\\ 1 & 0 \end{bmatrix} [11−10],当我们求一个向量经过复合变换后的坐标时,可以通过下图右边公式那样直接使用复合变换矩阵,而不需要像下图左边那样对向量连续施加两次单独的变换。

更一般地,对于矩阵乘法,我们就有了新的认识:他的几何意义是先施加一个变换,再施加另一个变换,施加顺序从右到左,顺序不同得到的结果也不同。

推广到更一般地数学含义: g ( f ( x ) ) g( f( x)) g(f(x))
根据前面章节学习到的知识,要想求线性变换对向量的作用,首先要得到变换后的基向量的坐标,让我们来看一个例子,假设连续施加两个线性变换 M 1 M_{1} M1和 M 2 M_{2} M2。
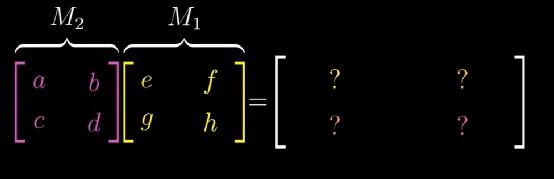
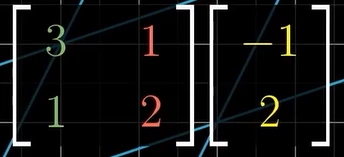
要想跟踪 i ⃗ \vec{i} i的去向,先看 M 1 M_{1} M1的第一列,这是经过 M 1 M_{1} M1变换后 i ⃗ \vec{i} i首先到达的地方: [ e g ] \begin{bmatrix} e\\ g \end{bmatrix} [eg],然后新的 i ⃗ \vec{i} i要经过 M 2 M_{2} M2的变换后到达最终目的地:
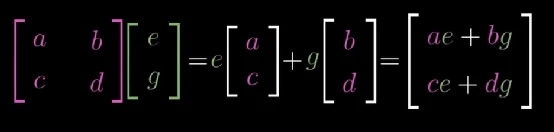
该结果作为复合矩阵的第一列, j ⃗ \vec{j} j经过同样的变换过程到达最终目的地,结果为复合变换矩阵第二列,复合变换的最终结果为:
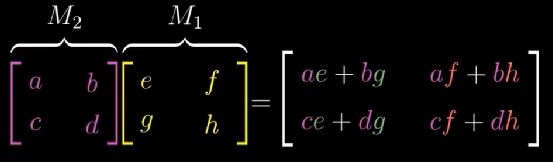
看,这不就是课堂上老师教的矩阵乘法计算规则嘛,只不过我们是从几何的角度推出来的。
大家可以从几何的角度来自行分析一下矩阵乘法的法则:
交换律: M 1 M 2 ≠ M 2 M 1 M_{1} M_{2} \neq M_{2} M_{1} M1M2=M2M1
结合率:(AB)C=A(BC)
三维空间中的线性变换
前面一直在讨论二维情况,也就是将二维向量映射成二维向量,其实,只要掌握了二维线性变换的核心本质,就能轻松的扩展到更高维的空间中。
三维空间变换以三维向量为输入,以三维向量为输出,和二维向量一样,一个线性变换是在操纵三维空间中所有的点,变换后保持空间中网格线等距且原点不变。

与二维一样,三维线性变换也是由基向量的去向完全决定,只不过基向量由 i ⃗ \vec{i} i, j ⃗ \vec{j} j变成了 i ⃗ \vec{i} i, j ⃗ \vec{j} j, k ⃗ \vec{k} k,例如,我们得到变换后三个基向量的坐标,那么由三个新的基向量组成矩阵就是三维线性变换矩阵 [ 1 1 1 0 1 0 − 1 0 1 ] \begin{bmatrix} 1 & 1 & 1\\ 0 & 1 & 0\\ -1 & 0 & 1 \end{bmatrix} 10−1110101 。
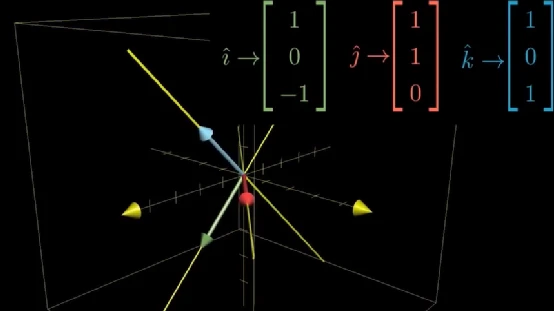
要想计算一个向量经过上面的三维变换后的新坐标,同样可以参照二维空间的计算方式,结果向量是基向量的线性组合。
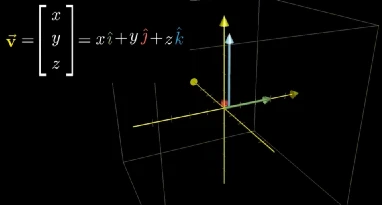
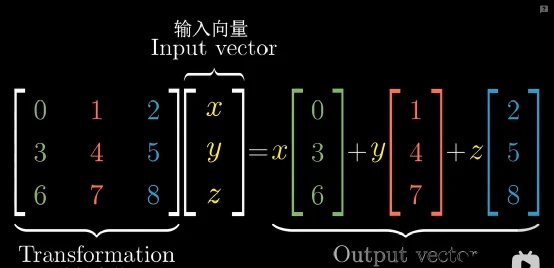
同理两个三维矩阵的相乘也可以合并成一个复合变换矩阵,三维变换在计算机图形学中有着广泛的应用。
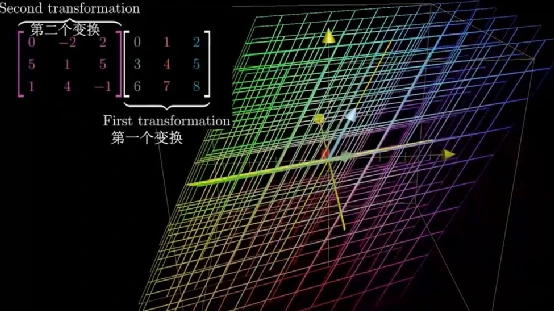
三维矩阵的乘法同样遵循二维矩阵乘法的思路。
行列式
前面我们从几何的角度对线性变换有了很直观的认识,其中有的线性变换对空间向外拉伸,有的则是将空间向内挤压。
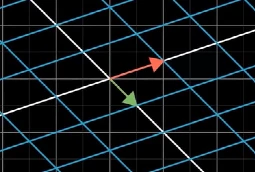
向内挤压
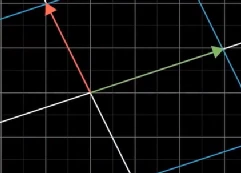
向外拉伸
有一种方法对于理解这些线性变换很有用,那就是准确测量向内挤压了多少,向外拉伸了多少,更具体地讲就是计算出一个区域增大或减少的比例。
让我们来看一个例子,假设一个线性变换矩阵 [ 3 0 0 2 ] \begin{bmatrix} 3 & 0\\ 0 & 2 \end{bmatrix} [3002],变换前基向量形成的四边形面积为1。
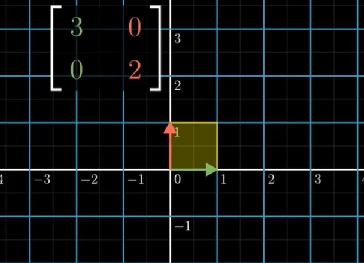
变换后,如下图,基向量形成一个2*3的矩形,面积为6
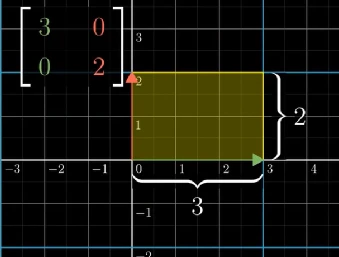
所以我们说这个变换将基向量形成的方格拉伸了6倍,根据线性变换的性质,如下图,所有可形成的区域都被拉伸了同样的大小。
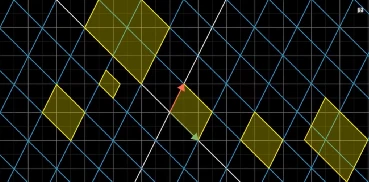
现在,我们要抛出一个重磅信息:这个面积的变化的比例值就是该线性变换矩阵的行列式,这就是行列式的几何意义。

如果行列式值大于1,则代表该线性变换矩阵将一个区域进行拉伸,大于0且小于1的数代表缩小,负数代表反方向缩放。
注意,如果一个线性变换矩阵的行列式为0,则代表该变换将一个区域压缩成了一条线或者是一个点,从几何意义上讲,也就是说该变换将空间压缩到了更小的维度上,这在我们后面判断线性方程组是否有解提供了重要依据。

同理,三维线性变换的行列式代表的则是体积的变换比例,如下图,一个以初始基向量形成的111的立方体经过线性变换后该体积变成了如下图的大小。
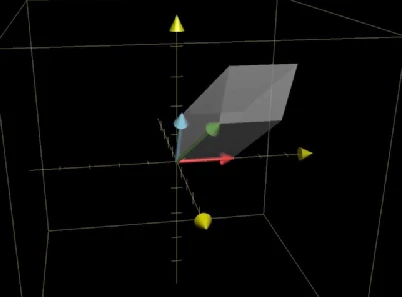
三维变换矩阵的行列式为0,代表空间被压缩成了一个面,或者一个点,如果行列式是负数,说明空间定向已经发生改变,不能用右手定则描述基向量之间的关系。
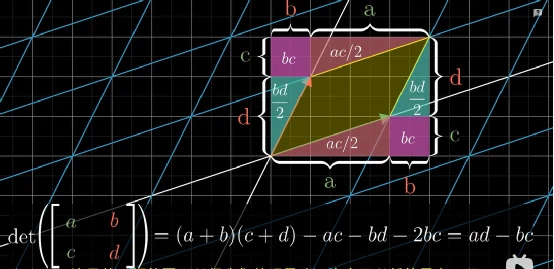
前面说了行列式的几何意义,那如何求一个矩阵的行列式呢?
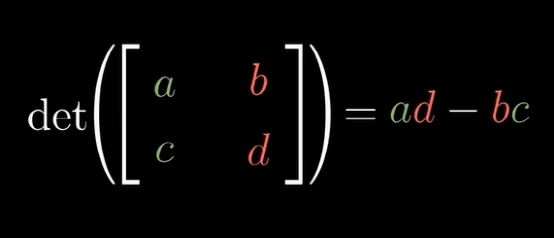
上图是一个行列式的计算公式,那它的几何意义是什么呢?如下图,假设给定一个特殊矩阵 [ a 0 0 d ] \begin{bmatrix} a & 0\\ 0 & d \end{bmatrix} [a00d], i ⃗ \vec{i} i被缩放了a倍, j ⃗ \vec{j} j被缩放了d倍,变换前后面积缩放了ad倍,这正符合行列式计算公式的结果。
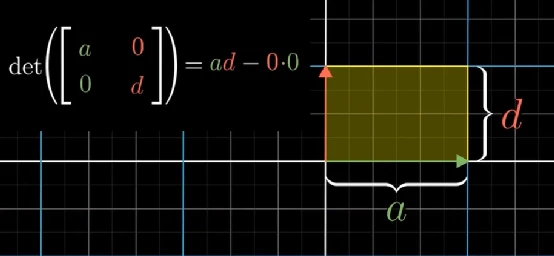
前面我们给出了一个特殊的例子,但推广到更一般的矩阵,也是满足上面公式的。