文章目录
- Center Smoothing: Certified Robustness for Networks with Structured Outputs
- Summary
- Research Objective
- Problem Statement
- Methods
- Evaluation
- Conclusion
- Notes
- Gaussian Smoothing
- 常用希腊字母
- 霍夫丁不等式(Hoeffding's inequality)
- 1.简述
- 2.霍夫丁不等式
- 2.1.伯努利随机变量特例
- 2.2.一般形式
Center Smoothing: Certified Robustness for Networks with Structured Outputs
中心平滑:经过认证的具有结构化输出的网络的鲁棒性

Summary
写完笔记之后最后填,概述文章的内容,以后查阅笔记的时候先看这一段。
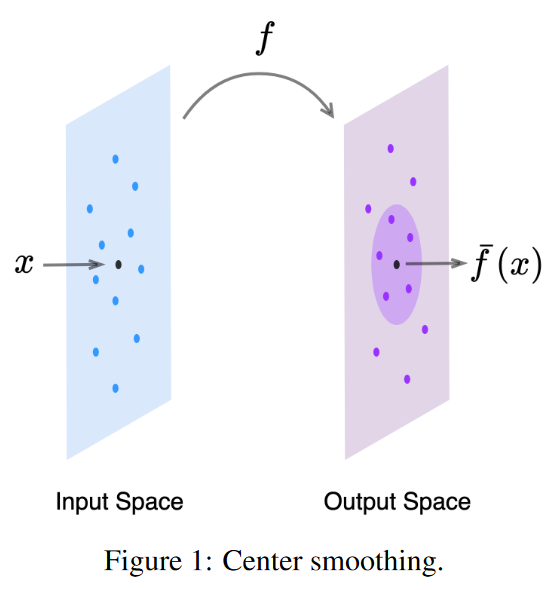
center smooth:对于给定的输入 x x x 与函数 f f f,以及对 x x x 的 l 2 l_2 l2 扰动半径 ϵ 1 \epsilon_1 ϵ1。中心平滑的目的是:在输出空间中计算一个最小半径为 r r r 的包围球,该球的球心为 f ˉ ( x ) \bar{f}(\boldsymbol{x}) fˉ(x),这时候的最小包围球包含至少一半的 f ( x + N ( 0 , σ c s 2 I ) ) f\left(\boldsymbol{x}+\mathcal{N}\left(0, \sigma_{c s}^2 I\right)\right) f(x+N(0,σcs2I))。这时候的 f ˉ \bar{f} fˉ 为 f f f 平滑函数, f ˉ ( x ) \bar{f}(\boldsymbol{x}) fˉ(x)为 f ( x ) f(x) f(x)在点 x x x 的平滑输出结果。整个过程如下表示:
∀ x ′ s.t. ∥ x − x ′ ∥ 2 ≤ ϵ 1 , d ( f ˉ ( x ) , f ˉ ( x ′ ) ) ≤ ϵ 2 \forall x^{\prime} \text { s.t. }\left\|x-x^{\prime}\right\|_2 \leq \epsilon_1, d\left(\bar{f}(x), \bar{f}\left(x^{\prime}\right)\right) \leq \epsilon_2 ∀x′ s.t. ∥x−x′∥2≤ϵ1,d(fˉ(x),fˉ(x′))≤ϵ2
意义在于:给定输入的扰动范围为 ϵ 1 \epsilon_1 ϵ1,经过平滑后的 f ˉ \bar{f} fˉ 能可证明地保证输出变化在 $ \epsilon_2$ 内。解决了 Randomized Smoothing只能局限于具有一维实值输出的分类任务和模型,从而能扩展到可证明的结构化输出(图像、文本、集合)问题。
Research Objective
作者的研究目标。
结构化输出(图像、文本、集合)的可证明鲁棒性
Problem Statement
问题陈述,要解决什么问题?
- 对于图像、文本、集合等结构化输出的问题,可证明的鲁棒性的目标是什么并不是很明显。
- 可证明的对抗鲁棒性研究主要局限于研究具有一维实值输出的分类任务和模型。
Methods
解决问题的方法/算法是什么?
- center smoothing:对于给定的输入 x x x,中心平滑使用高斯平滑分布对 x x x 附近的一组点进行采样,计算每个点上的函数值 f ( x ) f(x) f(x),并返回包含输出中至少一半点的最小球的中心空间。
- 为了优化上述问题,通过计算与样本中所有其他点的中值距离最小的点来近似中心空间的位置。
定义 P \mathcal P P 下 f f f 的平滑版本 f ˉ \bar{f} fˉ 作为在 M M M 中半径最小的球的中心,该球至少包含一半的 f ( x + P ) f (x + \mathcal P) f(x+P) 概率质量:
f ˉ P ( x ) = argmin z r s.t. P [ f ( X ) ∈ B ( z , r ) ] ≥ 1 2 \bar{f}_{\mathcal{P}}(x)=\underset{z}{\operatorname{argmin}} r \text { s.t. } \mathbb{P}[f(X) \in \mathcal{B}(z, r)] \geq \frac{1}{2} fˉP(x)=zargminr s.t. P[f(X)∈B(z,r)]≥21
B ( z , r ) = { z ′ ∣ d ( z , z ′ ) ≤ r } \mathcal{B}(z, r)=\left\{z^{\prime} \mid d\left(z, z^{\prime}\right) \leq r\right\} B(z,r)={z′∣d(z,z′)≤r}
- f ˉ \bar{f} fˉ 为 f f f 的平滑版本, f ( x ) f(x) f(x) 为 M M M中的一个输出元素
- P \mathcal P P 为平滑噪音的分布, δ \delta δ为每一个采样
- z z z 为输出空间 M M M 中的一个元素
- X = x + P X=x+\mathcal P X=x+P代表 x + δ x+\delta x+δ的概率分布,对于输入空间 D \mathcal D D 中的一个元素采样 x x x, 对其进行加平滑噪音
center smooth:
∀ x ′ s.t. ∥ x − x ′ ∥ 2 ≤ ϵ 1 , P [ f ( X ′ ) ∈ B ( f ˉ ( x ) , R ) ] > 1 2 \forall x^{\prime} \text { s.t. }\left\|x-x^{\prime}\right\|_2 \leq \epsilon_1, \mathbb{P}\left[f\left(X^{\prime}\right) \in \mathcal{B}(\bar{f}(x), R)\right]>\frac{1}{2} ∀x′ s.t. ∥x−x′∥2≤ϵ1,P[f(X′)∈B(fˉ(x),R)]>21
d ( f ˉ ( x ) , f ˉ ( x ′ ) ) ≤ 2 R d\left(\bar{f}(x), \bar{f}\left(x^{\prime}\right)\right) \leq 2 R d(fˉ(x),fˉ(x′))≤2R
d ( f ˉ ( x ) , f ˉ ( x ′ ) ) ≤ d ( f ˉ ( x ) , y ) + d ( y , f ˉ ( x ′ ) ) ≤ R + r ∗ ( x ′ ) \begin{aligned} d\left(\bar{f}(x), \bar{f}\left(x^{\prime}\right)\right) & \leq d(\bar{f}(x), y)+d\left(y, \bar{f}\left(x^{\prime}\right)\right) \\ & \leq R+r^*\left(x^{\prime}\right) \end{aligned} d(fˉ(x),fˉ(x′))≤d(fˉ(x),y)+d(y,fˉ(x′))≤R+r∗(x′)
r ∗ ( x ′ ) ≤ R r^*\left(x^{\prime}\right) \leq R r∗(x′)≤R
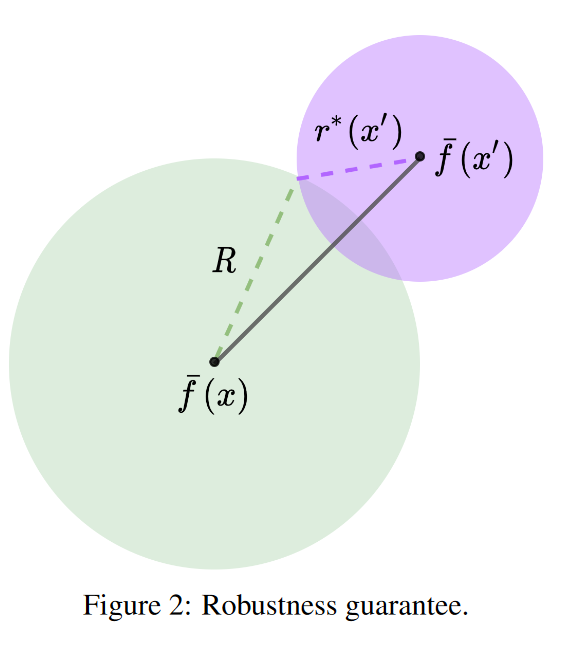
B ( f ˉ ( x ′ ) , r ∗ ( x ′ ) ) \mathcal{B}(\bar{f}(x'),r^*(x')) B(fˉ(x′),r∗(x′)): f ˉ ( x ′ ) \bar{f}(x') fˉ(x′) 为半径最小的球的中心,至少包含 f ( x ′ + P ) f (x' + P) f(x′+P) 概率质量的一半, r ∗ ( x ′ ) r^*(x') r∗(x′) 为最小半径的值
$ \mathcal{B}(\bar{f}(x),R) : : :\bar{f}(x)$ 为球的中心,对于所有满足 ∥ x − x ′ ∥ 2 ≤ ⋅ ϵ 1 \|x-x'\|_2\overset{\cdot}{\leq}\epsilon_1 ∥x−x′∥2≤⋅ϵ1 的 x ′ x′ x′,包含 f ( x ′ + P ) f (x′ + P) f(x′+P) 的概率质量的一半以上, R R R 为球的半径。
上述结果从理论上为我们提供了 f f f 的平滑版本 f ˉ \bar{f} fˉ,具有可证明的鲁棒性保证。因为经过平滑后的 f ˉ ( x ) \bar{f}(x) fˉ(x)与所有 f ( x + N ( 0 , σ c s 2 I ) ) f\left(\boldsymbol{x}+\mathcal{N}\left(0, \sigma_{c s}^2 I\right)\right) f(x+N(0,σcs2I))的中心距离能够被bound住,因为一个对抗扰动很难去改变 f ( x + N ( 0 , σ c s 2 I ) ) f\left(\boldsymbol{x}+\mathcal{N}\left(0, \sigma_{c s}^2 I\right)\right) f(x+N(0,σcs2I))的中心,所以平滑版本的 f ˉ \bar{f} fˉ能够保证输出的变化的上限。
Evaluation
作者如何评估自己的方法,有没有问题或者可以借鉴的地方。
Conclusion
作者给了哪些strong conclusion, 又给了哪些weak conclusion?
Notes
在这些框架外额外需要记录的笔记。
Gaussian Smoothing
h ˉ ( x ) = argmax c ∈ Y P [ h ( x + δ ) = c ] \bar{h}(x)=\underset{c \in \mathcal{Y}}{\operatorname{argmax}} \mathbb{P}[h(x+\delta)=c] hˉ(x)=c∈YargmaxP[h(x+δ)=c]
p ϵ = Φ ( Φ − 1 ( p ) − ϵ / σ ) p_\epsilon=\Phi\left(\Phi^{-1}(p)-\epsilon / \sigma\right) pϵ=Φ(Φ−1(p)−ϵ/σ)
累计分布函数 Φ \Phi Φ(CDF)是概率分布函数(PDF)的积分。这很好理解。
逆累计分布函数 Φ − 1 \Phi^{-1} Φ−1(ICDF)简单地说,是累计分布函数的反函数。
CDF:已知横轴(某一事件)(值)求纵轴(概率);
ICDF:已知纵轴(概率)求横轴(某一事件)(值);
常用希腊字母
以下是常用希腊字母及其在数学、统计学和科学中的读法:
- α (alpha):常用表示显著性水平,一般读作 “阿尔法”。
- β (beta):常用表示回归系数或错误率,读作 “贝塔”。
- γ (gamma):常用表示形状参数或比率,读作 “伽玛”。
- δ (delta):常用表示误差或变化量,读作 “德尔塔”。
- ε (epsilon):常用表示小量或误差项,读作 “艾普西隆”。
- ζ (zeta):常用表示 Riemann zeta 函数,读作 “泽塔”。
- η (eta):常用表示效应量或预测误差,读作 “艾塔”。
- θ (theta):常用表示角度或参数,读作 “西塔”。
- κ (kappa):常用表示柯西分布或相关系数,读作 “卡帕”。
- λ (lambda):常用表示特征值或密度函数,读作 “兰姆达”。
- μ (mu):常用表示均值或期望值,读作 “缪”。
- ν (nu):常用表示自由度或频率,读作 “纽”。
- ξ (xi):常用表示方差或未知量,读作 “克西”。
- π (pi):常用表示圆周率或概率密度函数,读作 “派”。
- ρ (rho):常用表示相关系数或密度函数,读作 “柔”。
- σ (sigma):常用表示标准差或方差,读作 “西格玛”。
- τ (tau):常用表示 Kendall tau 相关系数或时间常数,读作 “陶”。
- υ (upsilon):常用表示假设检验中的自由度,读作 “宇普西隆”。
- φ (phi):常用表示正态分布的概率密度函数,读作 “斐”。
- χ (chi):常用表示卡方分布,读作 “卡伊”。
- ψ (psi):常用表示角度函数或叶赛尔函数,读作 “普赛”。
- ω (omega):常用表示角频率或参数,读作 “欧米伽”。
霍夫丁不等式(Hoeffding’s inequality)
1.简述
在概率论中,霍夫丁不等式给出了随机变量的和与其期望值偏差的概率上限,该不等式被Wassily Hoeffding于1963年提出并证明。霍夫丁不等式是Azuma-Hoeffding不等式的特例,它比Sergei Bernstein于1923年证明的Bernstein不等式更具一般性。这几个不等式都是McDiarmid不等式的特例。
2.霍夫丁不等式
2.1.伯努利随机变量特例
掷硬币,假设正面朝上概率为 p ,反面朝上概率为 1-p ,投掷 n 次,则正面朝上次数的期望值为 np 。更进一步,有以下不等式:
P ( H ( n ) ≤ k ) = ∑ i = 0 k ( n i ) p i ( 1 − p ) n − i P(H(n) \le k)=\sum_{i=0}^k \binom{n}{i} p^i (1-p)^{n-i}\\ P(H(n)≤k)=i=0∑k(in)pi(1−p)n−i
其中, H(n) 是 n 次投掷中,正面朝上的次数。
对某一 ε > 0 \varepsilon>0 ε>0 ,有 k = ( p − ε ) n k=(p-\varepsilon)n k=(p−ε)n ,上述不等式确定的霍夫丁上界将会按照指数级变化:
P ( H ( n ) ≤ ( p − ε ) n ) ≤ e x p ( − 2 ε 2 n ) ( 2.1.1 ) P(H(n) \le (p-\varepsilon)n) \le exp(-2 \varepsilon^2n) \quad (2.1.1)\\ P(H(n)≤(p−ε)n)≤exp(−2ε2n)(2.1.1)
类似地,可以得到:
P ( H ( n ) ≥ ( p + ε ) n ) ≤ e x p ( − 2 ε 2 n ) ( 2.1.2 ) P(H(n) \ge (p+\varepsilon)n) \le exp(-2 \varepsilon^2n) \quad (2.1.2)\\ P(H(n)≥(p+ε)n)≤exp(−2ε2n)(2.1.2)
综合(2.1.1)(2.1.2),可得:
P ( ( p − ε ) n ≤ H ( n ) ≤ ( p + ε ) n ) ≥ 1 − 2 e x p ( − 2 ε 2 n ) ( 2.1.3 ) P((p-\varepsilon)n\le H(n) \le (p+\varepsilon)n) \ge 1-2exp(-2 \varepsilon^2n) \quad (2.1.3)\\ P((p−ε)n≤H(n)≤(p+ε)n)≥1−2exp(−2ε2n)(2.1.3)
令 ε = ln n / n \varepsilon=\sqrt{\ln{n}/n} ε=lnn/n ,代入(2.1.3),有:
P ( ∣ H ( n ) − p n ∣ ≤ ln n / n ) ≥ 1 − 2 e x p ( − 2 ln n ) = 1 − 2 / n 2 ( 2.1.4 ) P(|H(n)-pn|\le \sqrt{\ln{n}/n})\ge 1-2exp(-2\ln n)=1-2/n^2 \quad (2.1.4) P(∣H(n)−pn∣≤lnn/n)≥1−2exp(−2lnn)=1−2/n2(2.1.4)
(2.1.4)即为霍夫丁不等式的伯努利随机变量特例。
2.2.一般形式
令 X 1 , … , X n X_1,\dots,X_n X1,…,Xn 为独立的随机变量,且 X i ∈ [ a , b ] , i = 1 , … , n X_i\in[a,b] , i=1,\dots,n Xi∈[a,b],i=1,…,n 。这些随机变量的经验均值可表示为:
X ˉ = X 1 + ⋯ + X n n \bar{X}=\frac{X_1+\dots+X_n}{n}\\ Xˉ=nX1+⋯+Xn
霍夫丁不等式叙述如下:
∀ t > 0 , P ( X ˉ − E [ X ˉ ] ≥ t ) ≤ e x p ( − 2 n 2 t 2 ∑ i = 1 n ( b i − a i ) 2 ) ( 2.2.1 ) \forall{t>0},\quad P(\bar{X}-E[\bar{X}]\ge t)\le exp(-\frac{2n^2t^2}{\begin{matrix} \sum_{i=1}^n (b_i-a_i)^2 \end{matrix}}) \quad(2.2.1)\\ ∀t>0,P(Xˉ−E[Xˉ]≥t)≤exp(−∑i=1n(bi−ai)22n2t2)(2.2.1)
令 X ˉ = − X ˉ \bar{X}=-\bar{X} Xˉ=−Xˉ ,代入上述不等式,可得:
∀ t > 0 , P ( E [ X ˉ ] − X ˉ ≥ t ) ≤ e x p ( − 2 n 2 t 2 ∑ i = 1 n ( b i − a i ) 2 ) ( 2.2.2 ) \forall{t>0},\quad P(E[\bar{X}]-\bar{X}\ge t)\le exp(-\frac{2n^2t^2}{\begin{matrix} \sum_{i=1}^n (b_i-a_i)^2 \end{matrix}}) \quad (2.2.2)\\ ∀t>0,P(E[Xˉ]−Xˉ≥t)≤exp(−∑i=1n(bi−ai)22n2t2)(2.2.2)
综合(2.2.1)(2.2.2),可得霍夫丁不等式的另一种形式:
∀ t > 0 , P ( ∣ X ˉ − E [ X ˉ ] ∣ ≥ t ) ≤ 2 e x p ( − 2 n 2 t 2 ∑ i = 1 n ( b i − a i ) 2 ) ( 2.2.3 ) \forall{t>0},\quad P(|\bar{X}-E[\bar{X}]|\ge t)\le 2exp(-\frac{2n^2t^2}{\begin{matrix} \sum_{i=1}^n (b_i-a_i)^2 \end{matrix}}) \quad (2.2.3)\\ ∀t>0,P(∣Xˉ−E[Xˉ]∣≥t)≤2exp(−∑i=1n(bi−ai)22n2t2)(2.2.3)
若令 S n = X 1 + ⋯ + X n S_n=X_1+\dots+X_n Sn=X1+⋯+Xn ,霍夫丁不等式可叙述为:
$$
\forall{t>0},\quad P(S_n-E[S_n]\ge t)\le exp(-\frac{2t^2}{\begin{matrix} \sum_{i=1}^n (b_i-a_i)^2 \end{matrix}}) \quad (2.2.4)\
\forall{t>0},\quad P(E[S_n]-S_n\ge t)\le exp(-\frac{2t^2}{\begin{matrix} \sum_{i=1}^n (b_i-a_i)^2 \end{matrix}}) \quad (2.2.5)\
\forall{t>0},\quad P(|S_n-E[S_n]|\ge t)\le 2exp(-\frac{2t^2}{\begin{matrix} \sum_{i=1}^n (b_i-a_i)^2 \end{matrix}}) \quad (2.2.6)\
$$
从(2.2.1)推导(2.2.4),只需对不等式 X ˉ − E [ X ˉ ] ≥ t \bar{X}-E[\bar{X}]\ge t Xˉ−E[Xˉ]≥t 左右两边同乘系数 n n n ,再令 t = n t t=nt t=nt 即可。不难看出,当 X i X_i Xi 为伯努利随机变量时,(2.2.6)即可转化为(2.1.4)。
需要注意的是, X i X_i Xi 若为无放回抽样时的随机变量,该等式依然成立,尽管此时这些随机变量已不再独立。相关证明可查看Hoeffding在1963年发表的论文。在无放回抽样时,若想要更好的概率边界,可查看Serfling在1974年发表的论文。
学习链接:https://zhuanlan.zhihu.com/p/45342697
随机变量时,(2.2.6)即可转化为(2.1.4)。
需要注意的是, X i X_i Xi 若为无放回抽样时的随机变量,该等式依然成立,尽管此时这些随机变量已不再独立。相关证明可查看Hoeffding在1963年发表的论文。在无放回抽样时,若想要更好的概率边界,可查看Serfling在1974年发表的论文。
学习链接:https://zhuanlan.zhihu.com/p/45342697