物理驱动深度学习方法总结

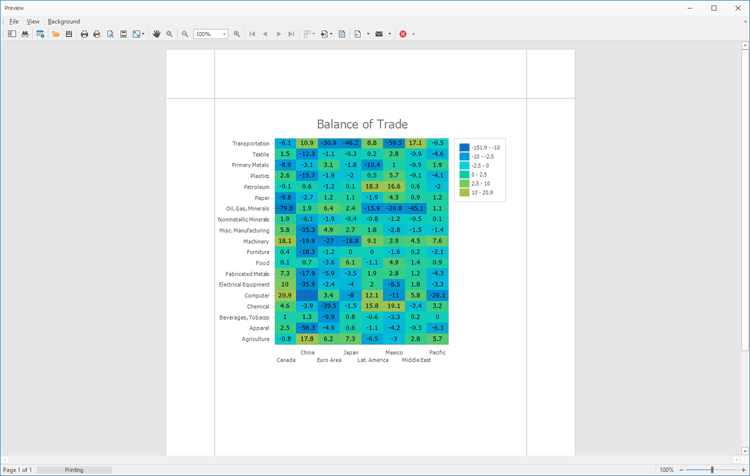
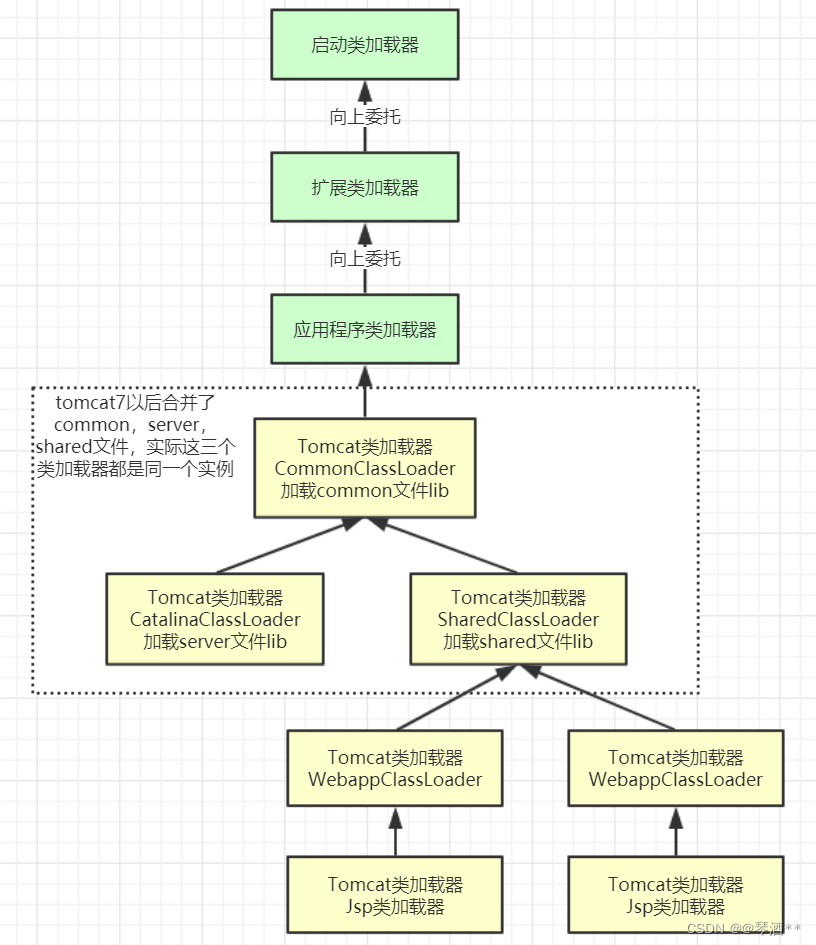
一、物理驱动深度学习方法总结

现有博主更新物理驱动深度学方法总体介绍
在这里插入图片描述
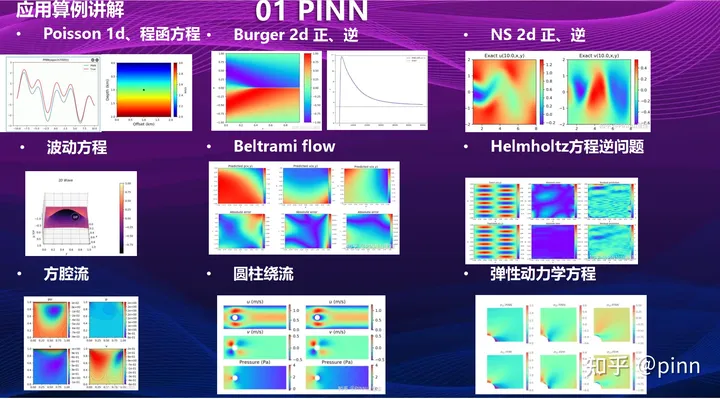
添加图片注释，不超过 140 字（可选）

二、 PINN介绍

PINN综述Blog介绍：内嵌物理知识神经网络（Physics Informed Neural Network，简称PINN）是一种科学机器在传统数值领域的应用方法，特别是用于解决与偏微分方程（PDE）相关的各种问题，包括方程求解、参数反演、模型发现、控制与优化等。
综述论文
Physics Informed Machine Learning – A Taxonomy and Survey of Integrating Prior Knowledge into Learning Systems
Integrating physics-based modeling with machine learning: A survey
Scientific Machine Learning through Physics-Informed Neural Networks: Where we are and What’s next
基于神经网络的偏微分方程求解方法研究综述，中文综述

三、基于神经网络的PDE方程求解编程教程

单个PDE求解：

1.PINN:

深度学习求解微分方程系列一：PINN求解框架（Poisson 1d）
深度学习求解微分方程系列二：PINN求解burger方程
深度学习求解微分方程系列三：PINN求解burger方程逆问题
深度学习求解微分方程系列四：基于自适应激活函数PINN求解burger方程逆问题
深度学习求解微分方程系列五：PINN求解Navier-Stokes方程正逆问题
深度学习求解微分方程系列六：PINN求解波动方程
深度学习求解微分方程系列七：PINN求解Beltrami flow方程
深度学习求解微分方程系列八：PINN求解Helmholtz方程逆问题
深度学习求解微分方程系列九：PINN求解方腔流问题
深度学习求解微分方程系列十：PINN求解稳态非稳态圆柱绕流问题
深度学习求解微分方程系列十一：硬边界约束的PINN求解弹性动力学方程(平面应力，弹性波传播)
深度学习求解微分方程系列十二：PINN求解程函方程
深度学习求解微分方程系列十三：PINN求解线弹方程正逆问题

2.物理信息极限学习机

一种基于物理信息极限学习机的PDE求解方法
一种基于物理信息极限学习机的PDE求解方法—helmholtz方程逆问题
一种基于物理信息极限学习机的PDE求解方法—扩散方程
一种基于物理信息极限学习机的PDE求解方法—对流方程
一种基于物理信息极限学习机的PDE求解方法—Biharmonic方程正逆问题

3.贝叶斯物理信息极限学习机

一种基于贝叶斯物理信息极限学习机的PDE求解方法—扩散方程

4.PINN改进方法

一种基于自适应激活函数的PINN求解方法
一种基于域分解的加权PINN——流体冲击管(欧拉方程)问题
一种面向噪声和异常数据下的鲁棒PINN方法
一种自适应权重的PINN方法

5.一种用于时空PDE的内嵌物理卷积循环神经网络

结合物理信息，利用CNN和LSTM求解时序微分方程。

求解参数化PDE

1.Deeponet

神经算子（一）：DeepOnet模型解析及复现

2 物理驱动深度学习方法

一种物理驱动深度学习方法求解麦克斯韦方程(Maxwell’s equations)——物理信息CNN

3.基于降阶模型的方法

一种基于POD和神经网络的代理模型方法

四、物理驱动深度学习方法几点讨论

具体请看对应链接详细解释。
具体请看对应链接详细解释。

1 物理信息驱动的深度学习相比于传统数值方法的潜在优势

反问题计算上有比较大的优势。
需要做快速推断时，优势更明显。
高维问题上的潜在优势。

2 先验物理嵌入深度学习模型研究重要进展和趋势

物理嵌入方式方法上。当前，物理信息驱动的深度学习方法主要有以下几种物理嵌入的方式：
- 通过对网络结构特殊设计嵌入物理。如已知微分方程有一阶导和二阶导，可将一阶导和二阶导嵌入到网络模型中，这可以看做是一种直觉的嵌入，能够提高网络的学习，但这并不是必须地，一定能提高网络学习能力，而是直觉上觉得应该能提高。
- 某种意义上的hard constraint。
- 从网络学习上。
- 很多知识通过数据隐式表现（如模拟数据）如何利用这些数据。
量化不确定性。

3 神经网络在求解PDE-based物理系统时的重要理论问题

从频率角度看待收敛性问题。
适定性问题研究。
损失震荡持续下降问题。特别是利用神经网络求解PDE时，
如何在不训练网络下做误差分析，给出网络的一些收敛阶。

4 面临的理论、算法和应用方面的主要挑战与可能的解决方法

严格嵌入物理。物理信息不是简单加到损失函数中进行优化，而且设计网络时，严格嵌入网络结构中，使得网络输入输出严格满足物理约束，再去做优化。一种思路，能否将传统数值方法优势叠加到网络设计中可能使得求解优化问题变得更简单，也是当前研究一大难点。
应用上可进一步发展。理论上进一步难做，但目前来看，往应用问题上进一步发展还是非常有前景。物理驱动深度学习方法在前面讲到在逆问题上的优势，对于传统数值方法在某些逆问题上很难求解甚至无法求解，但利用深度学习神经网络的灵活性，能求解以前不能做的问题并将误差降到勉强能接受的问题。
benchmark的研究。提出的方法能够在同样的问题上验证算法。
关注频率角度看待网络学习。可以关注学习上海交大许志钦老师的blog，频率原则。