模型处理过程:

一. 问题引入
基于学习的MVS算法因为受到显存的限制,输出的深度图的空间分辨率只有输入图像的1/16大小(长宽均为输入图像的1/4大小)。以MVSNet为例,对于1600×1184大小的输入图像,需要构建h×w×D×F=400×296×256×8大小的代价体,16GB的显卡才可以胜任。之前的方法限制了高分辨率MVS算法的发展。
那么问题来了,为什么要得到高分辨率的深度图呢?我们知道,MVS算法的评测是对最后生成的点云进行评测。同等情况下,深度图分辨率越高,得到的空间3D点数目越多,那么点云的完整性会更高,重建质量则更佳。

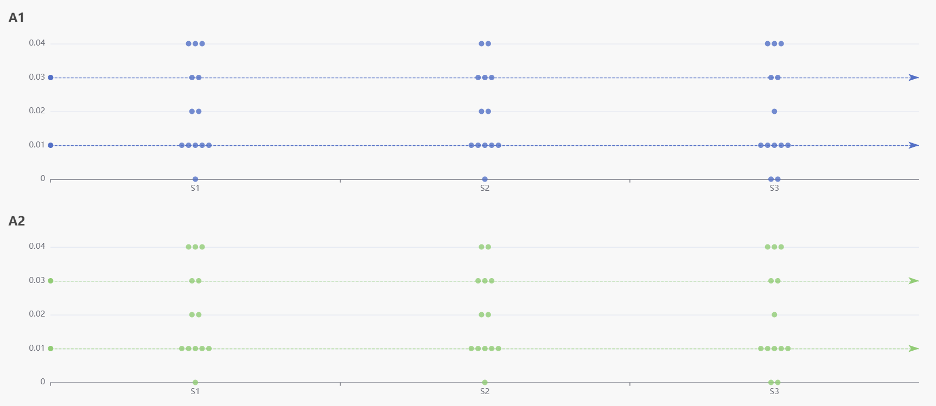
显示了分辨率为W×H×D×F的标准成本体积,其中W×H表示空间分辨率,D是平面假设的数量,F是特征图的通道数量 ,I为深度间隔
关于代价体:代价体(Cost Volume)是三维的,存储时为4D的tensor。我们可以理解为:代价体每一个位置存储的是一个F维的向量而不是标量。如图2所示,空间分辨率H×W越高,平面假设数D越多,深度间隔I越小,那么得到的深度图质量越高;同时显存占用越大、耗时越长。那么,有没有一种可以权衡精度和效率的方法呢?
为了解决上述问题,我们提出了一个级联成本-体积公式,并以粗略到精细的方式预测代价体。
二. 模型结构
整体思路:CasMVSNet使用级联的代价体来实现coarse-to-fine【 由粗到细 】的深度估计。
具体地,首先通过一个较小的代价体估计低分辨率的深度图,然后可以根据上一级输出的深度图,缩减当前尺度的深度假设范围。
CasMVSNet使用3级的代价体来实现深度图估计,包括两级的中间结果和一个最终的深度输出。

1. 特征提取模块
CasMVSNet需要在每个尺度上都进行特征提取和代价体构建,所以需要输入图像的多尺度特征。文章使用了三个尺度的FPN(Feature Pyramid Network)网络。 采用具有更高空间分辨率的特征图来构建更高分辨率的成本量 ,三个尺度的特征图空间分辨率分别为输入图像的{1/16, 1/4, 1}大小。和之前的方法一样,不同输入图像之间共享权重。

2. 深度范围的确定

R1表示的第一阶段的深度(或视差)范围覆盖了输入场景的整个深度(或差异)范围。
I为深度间隔
最低分辨率:将整个场景的深度范围离散D1个平面【本文中D1=48】,如上图1所示,其中粉色直线为深度假设平面,黄色曲线为估计的深度图。
Rk+1=Rk·wk,其中Rk是第k阶段的假设范围,wk<1是假设范围的缩小因子。
Ik+1=Ik·pk,其中Ik是第k阶段的假设平面区间,pk<1是假设平面区间的缩减因子。
给定假设范围Rk和假设平面间隔Ik ,相应的假设平面数目Dk=Rk/Ik
前面问题引入部分说明了,Dk越多,会导致GPU内存和运行时间的增加 ,基于级联公式,我们可以有效地减少假设平面的总数,因为假设范围(Rk)逐阶段显著减少,同时仍然覆盖整个输出范围。
后面的尺寸:如图2所示,级联成本体积可以基于前一阶段的预测输出,缩小假设范围【Rk】。
以上一阶段估计的深度图为中心,取一定固定深度范围Rk, 确定每一像素位置处的dmin和dmax, 其中dk-1为上一阶段上采样后的深度图,Rk为当前尺度的深度假设范围,然后根据场景范围离散处Dk个深度平面【本文中D2=32,D3=8】,不同像素点的深度范围可以不一样
上一阶段的输出【推测深度图】会被送到下一阶段中和下一阶段的尺度特征图空间一起作为下一阶段的单应性变换的输入

3. 单应性变换

其中dm k表示在第k阶段的第m个像素的预测深度,∆m k+1是在第k+1阶段要学习的第m像素的残差深度。 对于原始MVSNet所使用的单应性矩阵,只是修改了d的底数
4. 损失计算

损失函数为3个尺寸深度图的L1损失的加权和,不同尺寸不同的权重,空间分辨率越高的尺幅权重越大,具体的,【λ1, λ2, λ3】分别被设置成了【0.5, 1.0, 1.5】
特征匹配和代价聚合和深度图回归
同MVSNet