腾讯云作为国内领先的云服务提供商,不仅为用户提供稳定可靠的云服务器,还为新用户带来了一系列的优惠活动和代金券,以降低购买成本,提高业务效益。在这里,我们将为您详细介绍腾讯云服务器的新人优惠活动及代金券,并为您提供一些建议,希望能够帮助您选择合适的配置和云产品,充分利用腾讯云的优惠政策和特惠。
腾讯云双十一领9999代金券 https://1111.mian100.cn
腾讯云新用户领2860代金券 https://xinke.mian100.cn
腾讯云3年时长、5年时长优惠服务器尽享新用户优惠 https://5nian.mian100.cn
腾讯云服务器的新人优惠活动只能享受一次,这对于一些已经购买过腾讯云服务器的老客户来说或许有些遗憾。但是,如果您的家人或朋友还没有购买腾讯云服务器,他们可以作为新人享受优惠折扣。
多种优惠活动和代金券提供选择
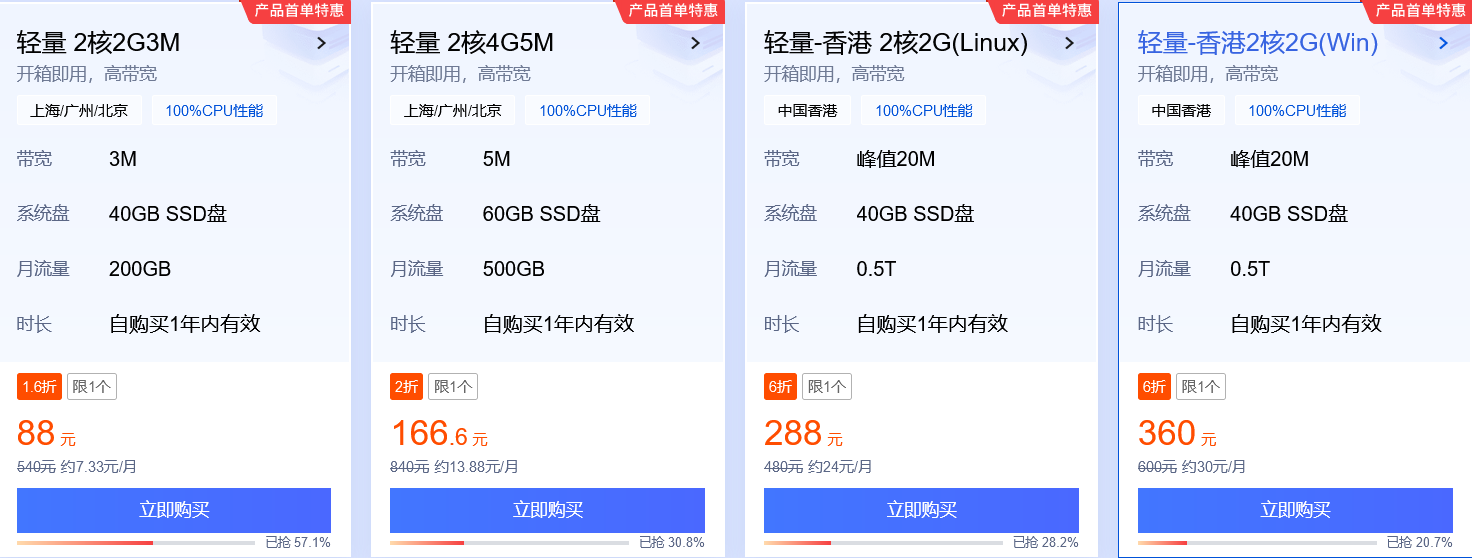
腾讯云为用户提供了多种优惠活动和代金券,以满足不同用户的需求。比如,2核2G3M云服务器仅需88元/年,4核8G云服务器仅需6490.44元/5年。这些优惠价格相比于市场价都有很大的优势,能够帮助用户降低购买成本。此外,腾讯云还提供了代金券优惠,如9999元代金券大礼包和新人2860元代金券大礼包。用户可以根据自身需求选择适合自己的优惠活动和代金券,进一步降低购买成本。
腾讯云88元/年服务器配置查看 https://tengxun.mian100.cn
腾讯云3年时长、5年时长优惠服务器尽享新用户优惠 https://5nian.mian100.cn
合理选择配置和云产品,充分利用优惠政策和特惠
在享受腾讯云服务器的优惠活动时,我们还应该根据自身需求选择合适的配置和云产品。腾讯云提供了多种不同配置的服务器,满足不同用户的需求。我们应该根据自己的业务需求和预算,选择适合的服务器配置,以充分发挥腾讯云服务器的性能和效益。
同时,我们也要充分利用腾讯云的优惠政策和特惠,如新人优惠活动、代金券等,以降低购买成本。这些优惠政策和特惠是腾讯云为用户提供的福利,我们应该积极参与,合理规划购买时间和方式,以获取更多的优惠。