6.9平衡二叉树（LC110-E）

绝对值函数：abs()

算法：

高度和深度的区别：

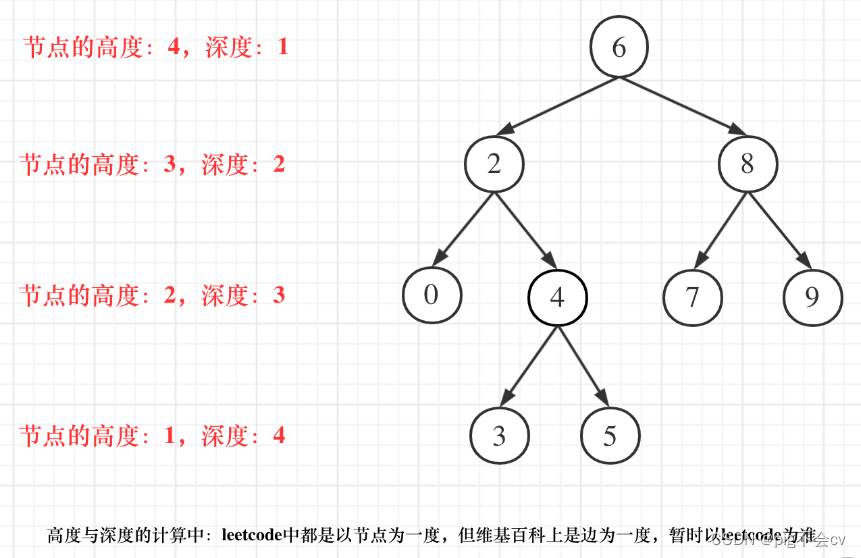
节点的高度：节点到叶子节点的距离（从下往上）

节点的深度：节点到根节点的距离（从上往下）

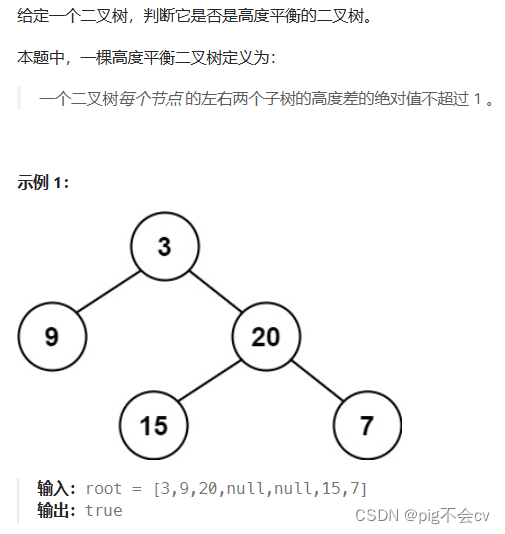
逻辑：一个平衡二叉树的每个节点的左右子树都是平衡二叉树

调试过程：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def isBalanced(self, root: Optional[TreeNode]) -> bool:if self.getheight(root) == 0:return Trueelse:return Falsedef getheight(self, node) -> int:if node == None:return 0        leftheight = self.getheight(node.left)rightheight = self.getheight(node.right)#左子树若有不平衡的，就返回-1if leftheight == -1:return -1#右子树若有不平衡的，就返回-1if rightheight == -1:return -1if abs(leftheight-rightheight)>1:return -1else:return 0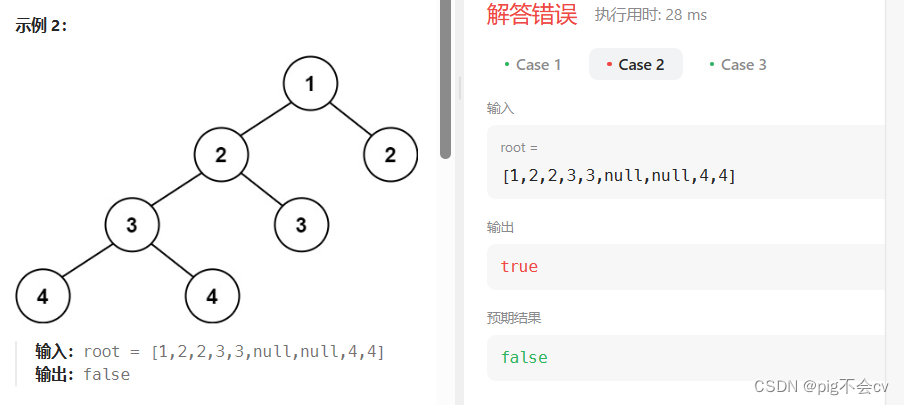

原因：问题出在return 0上面，改成return 1 + max(leftheight, rightheight)就好了

`return 0`的含义是将节点的高度设置为0，这是不正确的。

正确的做法是使用`return 1 + max(leftheight, rightheight)`来计算节点的高度。这里的`max(leftheight, rightheight)`表示选择左子树和右子树中较大的高度作为当前节点的高度，然后再加上1，表示当前节点的高度。

通过这种方式，我们可以确保节点的高度正确地传递到父节点，并在比较节点的高度差时得到正确的结果。如果节点的左子树和右子树高度差超过1，那么在递归过程中会返回-1，最终导致`isBalanced`函数返回False。

正确代码：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def isBalanced(self, root: Optional[TreeNode]) -> bool:if self.getheight(root) != -1:return Trueelse:return Falsedef getheight(self, node) -> int:if node == None:return 0        leftheight = self.getheight(node.left)rightheight = self.getheight(node.right)#左子树若有不平衡的，就返回-1if leftheight == -1:return -1#右子树若有不平衡的，就返回-1if rightheight == -1:return -1if abs(leftheight-rightheight)>1:return -1else:return 1 + max(leftheight, rightheight)

时间空间复杂度：
时间复杂度：

`isBalanced`函数中，我们调用了`getheight`函数来计算每个节点的高度。在最坏情况下，需要遍历二叉树的所有节点，因此时间复杂度为O(n)，其中n是二叉树中的节点数。
`getheight`函数是一个递归函数，它会遍历二叉树的所有节点。对于每个节点，我们需要递归地计算其左子树和右子树的高度，因此总的时间复杂度也是O(n)。
综上所述，整个算法的时间复杂度为O(n)。

空间复杂度：