选择题
T1. 执行以下代码,输出结果是()。
lst = "abc"
print(lst+lst)
- abcabc
- abc
- lst+lst
- abc+abc
T2. 执行以下代码,输出的结果是()。
age = {16,18,17}
print(type(sorted(age)))
-
<class 'set'> -
<class 'int'> -
<class 'str'> -
<class 'list'>
sorted(iterable, cmp=None, key=None, reverse=False)将返回一个新的list,不会改变原来的可迭代对象。
T3. 导入random标准库,执行print(random.randrange(2,20,2))语句,可能输出的结果是()。
- 2
- 5
- 13
- 20
random.randrange ([start,] stop [,step])
- 必须参数
stop表示随机生成的范围上限(不包括上限)start表示随机生成的范围下限(包括下限)step表示随机生成数之间的间隔,默认是1。
T4. 下列选项哪一个是转为整数的函数()?
-
str() -
int() -
float -
list()
T5. 以下关于Python中复数描述,错误的是()。
- 复数可以看作二元有序浮点数(x,y)
- 实部和虚部都是浮点数
- 虚数部分的后缀可以是"j",也可以是"J"
- 已知复数a,可以使用real获得虚数部分。
在Python中,复数类型用
complex表示。它可以通过以下方式创建:
- 直接指定实部和虚部:
complex(real, imag),real是实数部分,imag是虚数部分。- 使用字符串:
complex(string)例如:
a = complex(3, 4) # 创建一个复数3+4j a = complex('3+4j') # 创建一个复数3+4j
编程题
T1. N + N
问题描述
给定一个正整数 N N N,计算出 N + N N+N N+N的值。
例如: N = 4 N = 4 N=4, 4 + 4 4+4 4+4的值为 8 8 8。
输入描述
输入一个正整数 N N N
输出描述
输出 N + N N+N N+N的值
样例输入
4
样例输出
8
代码实现
n = int(input())
print(n + n)
T2. 字符
问题描述
给定一个只包含小写字母的字符串 S S S( S S S长度 ≥ 3 ≥3 ≥3),请输出字符串 S S S的第一个字符和最后一个字符。例如:
当S ="abc", a b c abc abc的第一个字符为 a a a,最后一个字符为 c c c,故输出 a c ac ac。
输入描述
输入一个只包含小写字母的字符串 S S S( S S S长度 ≥ 3 ≥3 ≥3)。
输出描述
输出字符串 S S S的第一个字符和最后一个字符,两个字符之间没有空格及其他字符
样例输入
abc
样例输出
ac
代码实现
s = input()
print(s[0] + s[-1])
T3. 数字币
问题描述
提示信息:合数指自然数中除了能被1和本身整除外,还能被其它正整数整除的数。例如 4 4 4, 4 4 4除了能被 1 1 1和 4 4 4整除,还可以被 2 2 2整除。
小明收藏了 N N N( 2 ≤ N ≤ 25 2≤N≤25 2≤N≤25)个数字币,每个数字币上都有一个面值(面值可以重复)。从数字币中任选 K K K( 2 ≤ K ≤ N 2≤K≤N 2≤K≤N)个,有多种选法,请将每次选择的数字币上的面值累加,然后解决以下两个问题:
- 问题1:累加的和中有多少种不同的结果
- 问题2:累加的和中有多少个不同的合数
例如: N = 5 N=5 N=5, K = 3 K=3 K=3, 5 5 5个数字币上的面值分别为 2 、 1 、 4 、 5 、 3 2、1、4、5、3 2、1、4、5、3,任选 3 3 3个数字币,有 10 10 10种选法,将每种选法上的面值累加: 2 + 1 + 4 = 7 、 2 + 1 + 5 = 8 、 2 + 1 + 3 = 6 、 2 + 4 + 5 = 11 、 2 + 4 + 3 = 9 、 2 + 5 + 3 = 10 、 1 + 4 + 5 = 10 、 1 + 4 + 3 = 8 、 1 + 5 + 3 = 9 、 4 + 5 + 3 = 12 2+1+4=7、2+1+5=8、2+1+3=6、2+4+5=11、2+4+3=9、2+5+3=10、1+4+5=10、1+4+3=8、1+5+3=9、4+5+3=12 2+1+4=7、2+1+5=8、2+1+3=6、2+4+5=11、2+4+3=9、2+5+3=10、1+4+5=10、1+4+3=8、1+5+3=9、4+5+3=12
其中累加的和中有 7 7 7种不同的结果,分别是 7 、 8 、 6 、 11 、 9 、 10 、 12 7、8、6、11、9、10、12 7、8、6、11、9、10、12;累加的和中有 5 5 5个不同的合数,分别是 8 、 6 、 9 、 10 、 12 8、6、9、10、12 8、6、9、10、12。
输入描述
第一行输入一个正整数 N N N( 2 ≤ N ≤ 25 2≤N≤25 2≤N≤25),表示数字币的个数。
第二行输入 N N N个正整数( 1 ≤ 1≤ 1≤正整数 ≤ 1000 ≤1000 ≤1000),表示数字币上的面值,正整数之间以一个英文逗号隔开。
第三行输入一个正整数 K K K( 2 ≤ K ≤ N 2≤K≤N 2≤K≤N),表示所要选取的数字币个数。
输出描述
输出两个整数,分别表示累加的和中不同结果的个数以及累加的结果中不同合数的个数,两个整数之间以一个英文逗号隔开。
样例输入
5
2,1,4,5,3
3
样例输出
7,5
代码实现
n = int(input())
a = eval(input())
k = int(input())
d = {}
ans1, ans2 = 0, 0
b = [0] * n
# 检查x是否为合数
def check(x):i = 2while i * i <= x:if x % i == 0:return Truei += 1return False
def dfs(t, last, s):if t == k:global ans1, ans2# 如果字典中不存在sif s not in d:d[s] = 1ans1 += 1# 检查是否为合数if check(s):ans2 += 1return;for i in range(last + 1, n):dfs(t + 1, i, s + a[i])
dfs(0, -1, 0)
print('%d,%d' % (ans1, ans2))
T4. 杨辉三角
问题描述
提示信息:杨辉三角就是一个用数排列起来的三角形(如下图),杨辉三角规则如下:
- 每行第一个数和最后一个数都为 1 1 1,其它每个数等于它左上方和右上方的两数之和;
- 第 n n n行有 n n n个数。
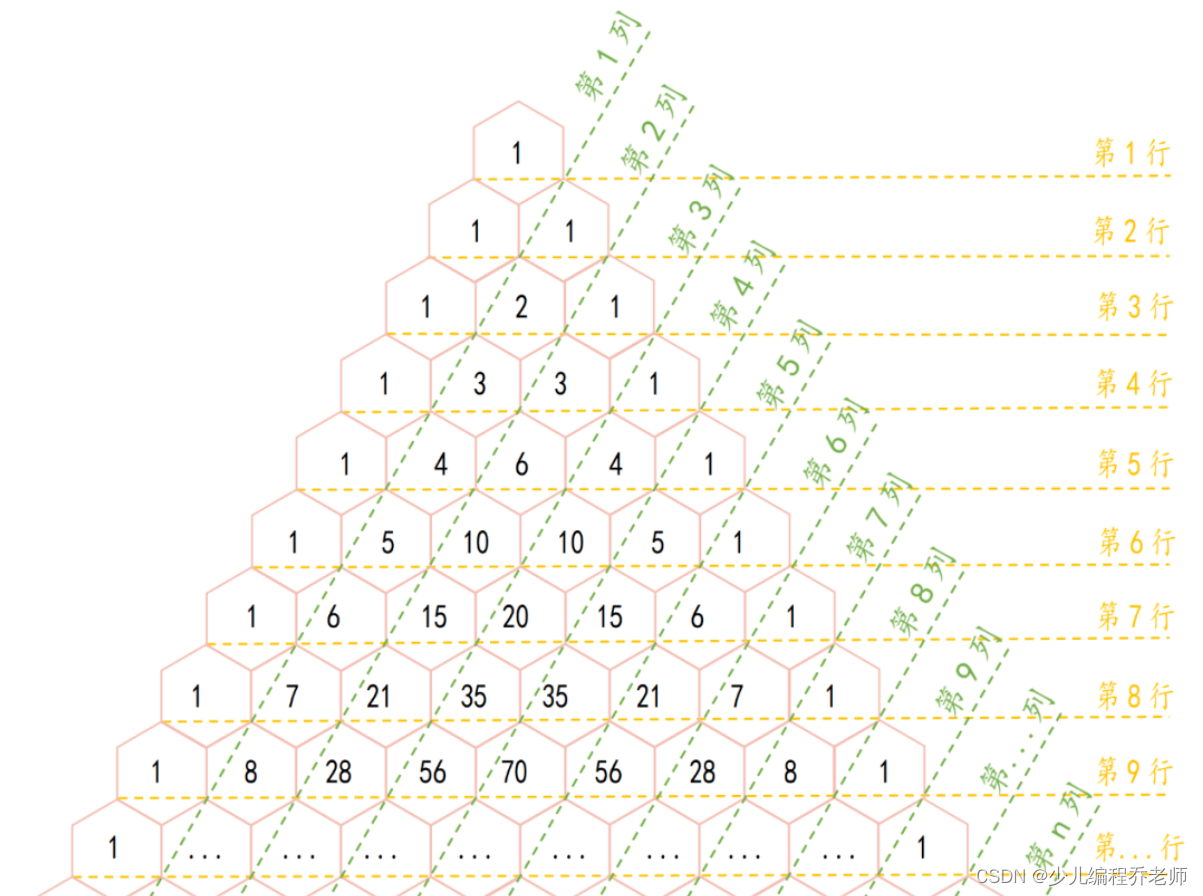
注意:“列”指的是如图所标注的斜列。
小青对杨辉三角的特点和规律研究得很明白,现要考察你对杨辉三角的熟悉程度,首先告知你这是一个 N N N行的杨辉三角,然后又告知了两个数值 X X X和 Y Y Y( X X X表示第几行, Y Y Y表示第几列),让你根据杨辉三角的特点和观察到的规律解决以下两个问题。
- 第 X X X行第 Y Y Y列对应的数是多少;
- 求出 N N N行的杨辉三角中第 Y Y Y列中所有数的和。
例如: N = 5 N=5 N=5, 5 5 5行的杨辉三角如下图。
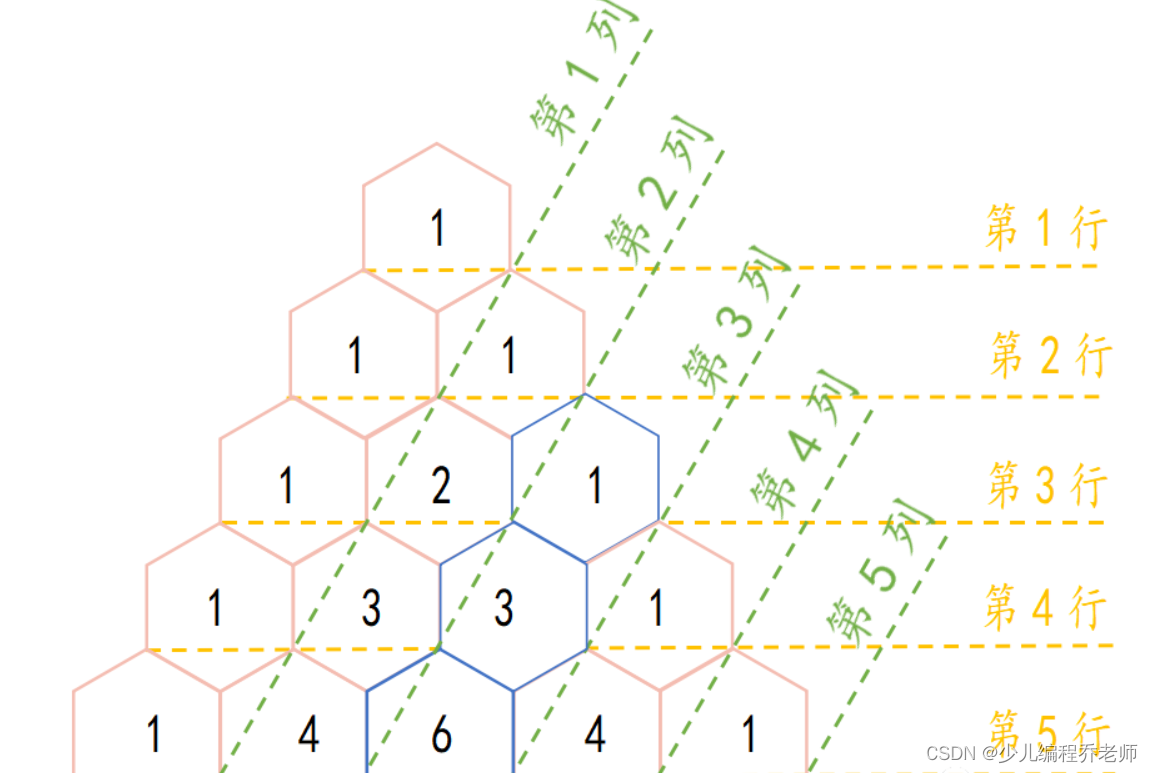
X = 5 X=5 X=5, Y = 3 Y=3 Y=3,第 5 5 5行第 3 3 3列对应的数为 6 6 6;第 3 3 3列中所有数的和为 10 10 10( 10 = 6 + 3 + 1 10 = 6 + 3 + 1 10=6+3+1)。
输入描述
第一行输入一个正整数 N N N( 2 ≤ N ≤ 30 2≤N≤30 2≤N≤30),表示杨辉三角的行数
第二行输入两个正整数 X X X和 Y Y Y( 1 ≤ Y ≤ X ≤ N 1≤Y≤X≤N 1≤Y≤X≤N),分别表示第 X X X行和第 Y Y Y列,正整数之间以一个英文逗号隔开。
输出描述
输出两个整数,分别表示 N N N行的杨辉三角中第 X X X行 Y Y Y列对应的数,及第 Y Y Y列上所有数的和,两个整数之间以一个英文逗号隔开。
样例输入
5
5,3
样例输出
6,10
代码实现
n = int(input())
x, y = eval(input())
# 初始化二维列表
f = [[0] * (n + 1) for _ in range(n + 1)]
# 计算杨辉三角,行列的下标从1开始
for i in range(1, n + 1):for j in range(1, i + 1):if i == 1 or j == i:f[i][j] = 1else:f[i][j] = f[i - 1][j] + f[i - 1][j - 1]
ans1 = f[x][y]
ans2 = 0
for i in range(1, n + 1):ans2 += f[i][y];
print('%d,%d' % (ans1, ans2))
T5. 涂鸦
问题描述
工人砌了一面奇特的砖墙,该墙由 N N N列砖组成( 1 ≤ N ≤ 1 0 6 1≤N≤10^6 1≤N≤106),且每列砖的数量为 K i K_i Ki( 1 ≤ K i ≤ 1 0 4 1≤K_i≤10^4 1≤Ki≤104,相邻两列砖之间无缝隙),每块砖的长宽高都为 1 1 1。
小蓝为了美化这面墙,需要在这面墙中找到一块面积最大的矩形用于涂鸦,那么请你帮助小蓝找出最大矩形,并输出其面积。
例如: N = 6 N = 6 N=6,表示这面墙有 6 6 6列,每列砖的数量依次为 3 、 2 、 1 、 5 、 6 、 2 3、2、1、5、6、2 3、2、1、5、6、2,如下图:
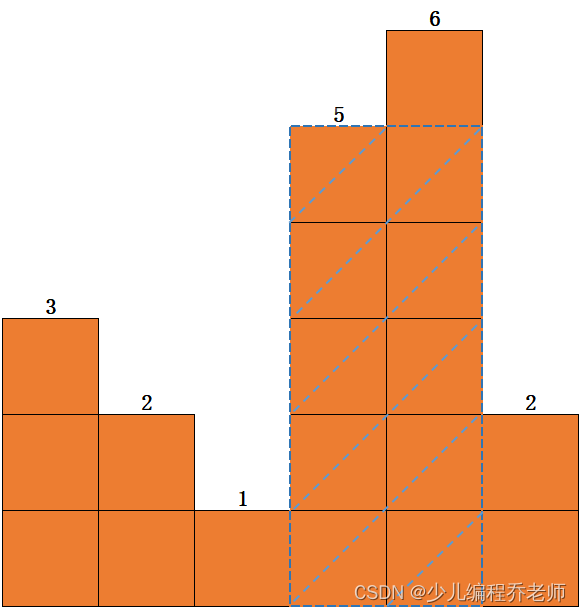
图中虚线部分是一块面积最大的矩形,其面积为 10 10 10。
输入描述
第一行输入一个正整数 N N N( 1 ≤ N ≤ 1 0 6 1≤N≤10^6 1≤N≤106),表示这面砖墙由几列砖组成
第二行输入 N N N个正整数 K i K_i Ki( 1 ≤ K i ≤ 1 0 4 1≤K_i≤10^4 1≤Ki≤104),表示每列砖的数量,正整数之间以一个空格隔开。
输出描述
输出一个正整数,表示最大矩形的面积。
样例输入
6
3 2 1 5 6 2
样例输出
10
算法思想1(60分,暴力枚举)
矩形的面积等于列数 × \times ×相邻列的高度最小值。因此可以暴力枚举所有相邻列的组合,计算其面积,然后打擂台求最大值即可。
时间复杂度
尝试所有相邻列的组合需要分别枚举开始列和结束列,时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
代码实现
n = int(input())
a = list(map(int, input().split()))
ans = 0
# 枚举矩形的开始列
for i in range(n):# 枚举矩形的结束列for j in range(i, n):# 从i到j一共有j - i + 1列,这些列中高度的最小值为min(a[i : j + 1]ans = max(ans, (j - i + 1) * min(a[i : j + 1]))
print(ans)
算法思想2(100分,枚举 + 单调栈)
矩形的面积等于每列砖的数量 × \times × 与它左右相邻的且具有相同高度的列数。因此可以枚举每列砖的数量,第 i i i列来说,不妨设其砖的数量为 a i a_i ai:
- 向左找到第一个小于 a i a_i ai的位置 L i L_i Li
- 向右找到第一个小于 a i a_i ai的位置 R i R_i Ri
此时以第 i i i列砖为高度的矩形的面积 = ( R i − L i − 1 ) × a i =(R_i - L_i-1)\times a_i =(Ri−Li−1)×ai,那么只需要打擂台求最大值即可。
那么如何向左(向右)找到第一个小于 a i a_i ai的位置呢,可以使用单调栈的思想,以 O ( 1 ) O(1) O(1)的时间复杂度实现。
时间复杂度
- 枚举每列砖的时间复杂度为 O ( n ) O(n) O(n)
- 单调栈向左(向右)找到第一个小于 a i a_i ai的位置的时间复杂度为 O ( 1 ) O(1) O(1)
总的时间复杂度为 O ( n ) O(n) O(n)。
代码实现
n = int(input())
a = list(map(int, input().split()))
L = [0] * n
R = [0] * n
# 单调栈查找左侧第一个小于a[i]的位置L[i]
stk = []
for i in range(n):while len(stk) != 0 and a[stk[-1]] >= a[i]:stk.pop()if len(stk) == 0: # 左侧没有比a[i]小的数L[i] = -1else:L[i] = stk[-1] # 栈顶就是左侧第一个比a[i]小的位置stk.append(i)
# 单调栈查找右侧第一个小于a[i]的位置R[i]
stk = []
for i in range(n - 1, -1, -1):while len(stk) != 0 and a[stk[-1]] >= a[i]:stk.pop()if len(stk) == 0: #右侧没有比a[i]小的数R[i] = nelse:R[i] = stk[-1] # 栈顶就是右侧第一个比a[i]小的位置stk.append(i)
ans = 0
for i in range(n):# (L, R)之间一共有R - L - 1列ans = max(ans, a[i] * (R[i] - L[i] - 1))
print(ans)T6. 传送门(仅中、高级组)
问题描述
在一个神奇空间里有 N N N个房间,房间从 1 1 1到 N N N编号,每个房间可能有一个或多个传送门,每个传送门都有一个编号,如果相同编号的传送门同时出现在多个房间中,表示这些房间可以互通。
给定两个房间的编号 A A A和 B B B,请找出从房间 A A A到达房间 B B B最少需要经过几个传送门。
例如: N = 3 N=3 N=3, 3 3 3个房间中传送门的编号分别为:
房间 1 1 1: 1 , 4 , 6 1,4,6 1,4,6;
房间 2 2 2: 2 , 3 , 4 , 8 2,3,4,8 2,3,4,8;
房间 3 3 3: 3 , 6 , 9 3,6,9 3,6,9。
其中房间 1 1 1和房间 2 2 2互通,共用 4 4 4号传送门;房间 1 1 1和房间 3 3 3互通,共用 6 6 6号传送门;房间 2 2 2和房间 3 3 3互通,共用 3 3 3号传送门;当 A = 1 A=1 A=1, B = 2 B=2 B=2,从房间 1 1 1到达房间 2 2 2,共有两种路线:
- 路线 1 1 1:从房间 1 1 1通过 4 4 4号传送门进入房间 2 2 2,共经过 1 1 1个传送门。如下图橙色路线所示。
- 路线 2 2 2:从房间 1 1 1通过 6 6 6号传送门进入房间 3 3 3,再从房间 3 3 3通过 3 3 3号传送门进入房间 2 2 2,共经过 2 2 2个传送门;故从房间 1 1 1到达房间 2 2 2最少需要经过 1 1 1个传送门。如下图黑色路线所示。

输入描述
第一行输入一个正整数 N N N( 2 ≤ N ≤ 20 2≤N≤20 2≤N≤20),表示房间数量。
接下来输入 N N N行,每行包含多个正整数( 1 ≤ 1≤ 1≤正整数 ≤ 100 ≤100 ≤100),第 2 2 2行到第 N + 1 N+1 N+1行依次表示 1 1 1到 N N N号房间内所有传送门的编号,正整数之间以一个英文逗号隔开。
最后一行输入两个正整数 A A A和 B B B( 1 ≤ A ≤ N , 1 ≤ B ≤ N 1≤A≤N,1≤B≤N 1≤A≤N,1≤B≤N,且 A ≠ B A≠B A=B),表示两个房间的编号,正整数之间以一个英文逗号隔开。
输出描述
输出一个整数,表示从房间 A A A到达房间 B B B最少需要经过几个传送门,如果房间 A A A不能到达房间 B B B,则输出 − 1 -1 −1
样例输入
3
1,4,6
2,3,4,8
3,6,9
1,2
样例输出
1
算法思想
- 首先,输入每个房间的传送门编号,可以计算出任意两个房间是否有传送门相连
- 然后,可以通过BFS求到起点 A A A的最短路径。
代码实现
n = int(input())
a = []
for i in range(n):b = eval(input())a.append(b)
A, B = eval(input())# g数组存储两个房间是否有传送门
g = [[0] * n for _ in range(n)]for i in range(n):for j in range(i + 1, n):for x in a[i]:if x in a[j]:# 第i个房间和第j个房间有传送门g[i][j] = g[j][i] = 1break
# bfs求最短路
ans = 0
st = [0] * n
q = [] # 队列
q.append((A, 0)) # 将起点和到起点的距离入队
st[A] = 1 # 将起点标记为已访问
# 只要队列不空,bfs计算到起点的最短路径
while len(q) != 0:x, d = q.pop(0)if(x == B): # 如果到达终点ans = dbreakfor i in range(n):# 如果i点已访问,或者x到i之间没有传送门if st[i] == 1 or g[x][i] == 0:continueq.append((i, d + 1))
print(ans)