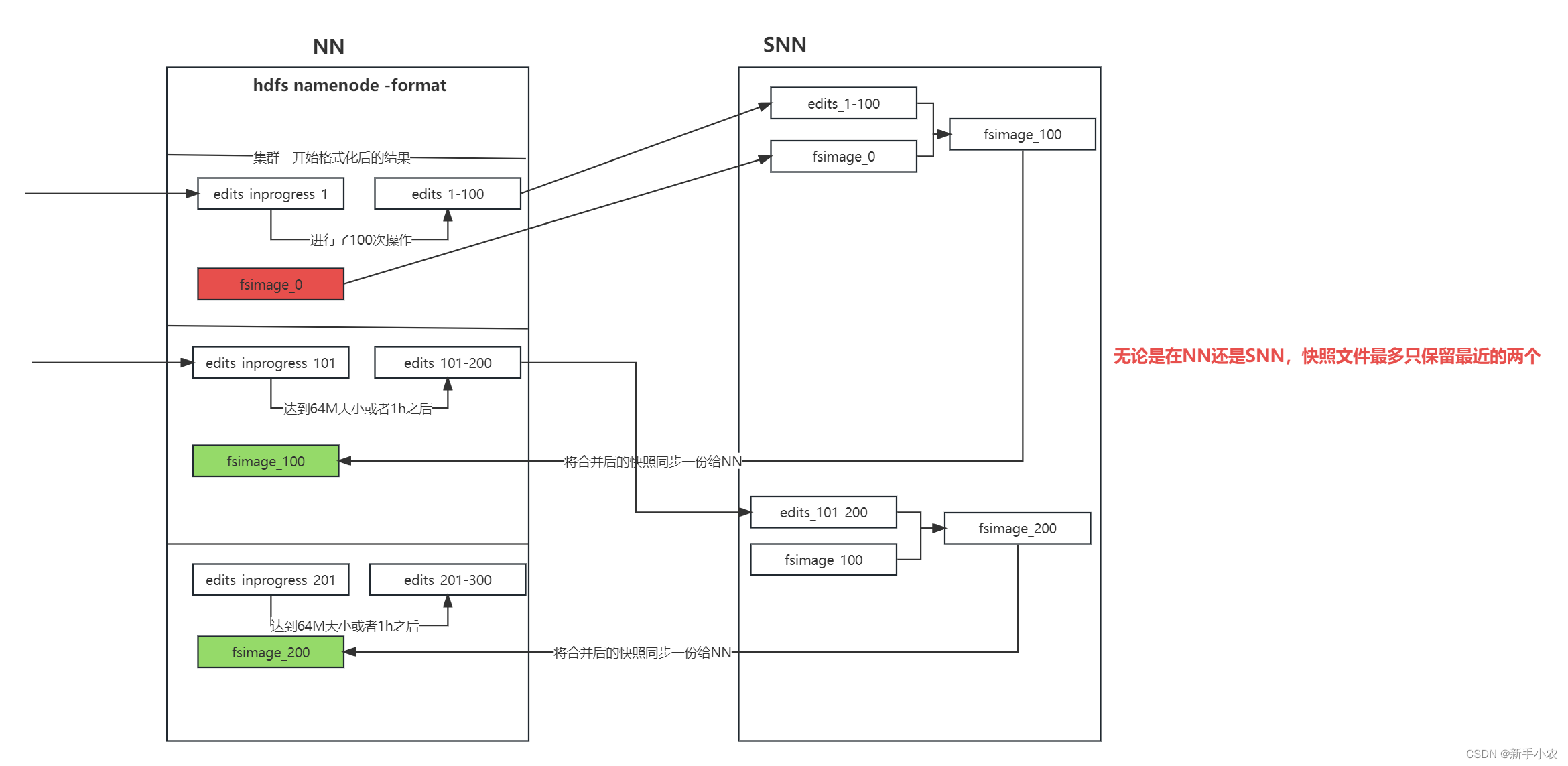
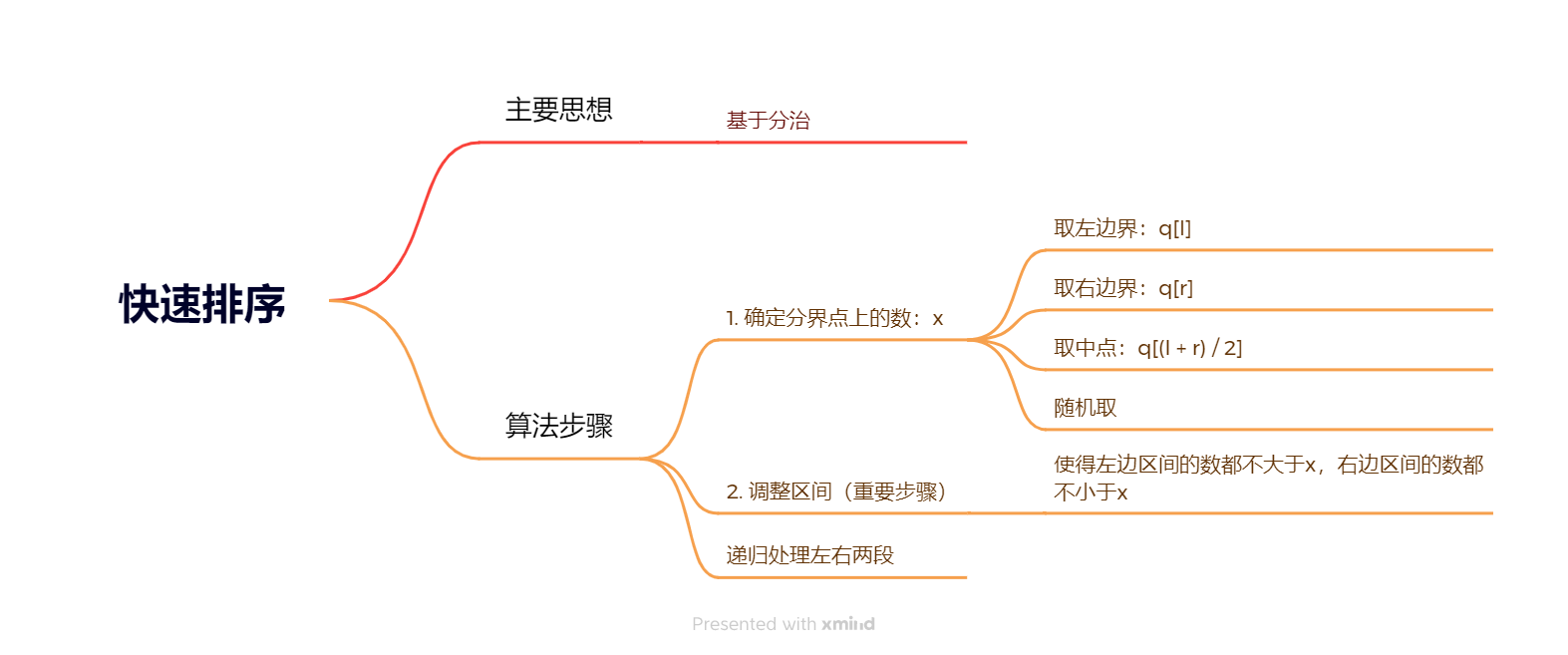
快速排序思维导图:
快速排序算法模版:
#include <iostream>using namespace std;const int N = 1e5 + 10;int n;
int q[N];void quick_sort(int q[], int l, int r)
{if (l >= r) return;int x = q[(l + r) / 2], i = l - 1, j = r + 1;while (i < j){do i++; while (q[i] < x);do j--; while (q[j] > x);if (i < j) swap(q[i], q[j]);}quick_sort(q, l, j);quick_sort(q, j + 1, r);
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i++) scanf("%d", &q[i]);quick_sort(q, 0, n - 1);for (int i = 0; i < n; i++) printf("%d ", q[i]);return 0;
}