【献给过去的自己】栈实现计算器（C语言）

背景

        记得在刚学C语言时，写了一篇栈实现计算器-CSDN博客文章。偶然间看到了文章的阅读量以及评论，居然有1.7w的展现和多条博友的点评，反馈。

        现在回过头来看，的确有许多不严谨的地方，毕竟当时分享文章时，还未毕业。理论和思维还不够严谨。但是我还依稀记得，班级上当时写出这个程序的同学，稀疏可数。所以在当时，还是有骄傲的资本的。本着对技术精益求精的态度，再通过本篇文章希望能够帮助刚接触C语言的朋友，也是给过去的自己一个满意的答复~

规则

        对于一个表达式，我们应该如何去识别它呢？当时，老师和我们说，按照如下规则进行解析即可。

        当时我们并不懂这个规则的由来，只知道按照这个规则去编程即可。再后来的工作中，因为考《软件设计师》资格证，了解到上述的规则，其实就是后缀表达式。同理还有前缀表达式，中缀表达式。

中缀表达式

        中缀表达式就是我们常用的一种算数表示方式。它的特点是操作符以中缀的方式处于操作数中间。但是中缀表达比较适合人类计算，对于计算机而言过于复杂。前缀表达式和后缀表达式对于计算机而言，更加友好。

        因此，我们想用程序实现计算器功能，有两种方式：

中缀表达式--> 前缀表达式-->计算

中缀表达式--> 后缀表达式-->计算

前缀表达式

        前缀表达式的运算符位于两个操作数之前，又称为前缀记法或波兰式。比如表达式（中缀）5+4，前缀表达式+ 5 4。因此使用前缀表达式进行计算，需要两个步骤。

  1. 如何将中缀表达式转换为前缀表达式

  2. 计算机如何识别前缀表达式并计算

中缀表达式转换前缀表达式

        根据文中描述，中缀表达式转换为前缀表达式的规则如下：

  1. 初始化两个栈：运算符栈S1和存储中间结果的栈S2;

  2. 从右至左扫描中缀表达式；

  3. 遇到操作数时，将其压入S2;

  4. 遇到运算符时，比较其与S1栈顶运算符的优先级；

    1. 如果S1为空，或栈顶运算符为右括号)，则将此运算符入栈；

    2. 否则，若优先级比栈顶运算符的较高或相等，也将运算符压入S1;

    3. 否则，将S1栈顶的运算符弹出并压入到S2,再次转到4.1与S1中新的栈顶运算符相比较；

  5. 遇到括号时：

    1. 如果是右括号)，则直接压入S1;

    2. 如果是左括号(，则依次弹出S1栈顶的运算符，并压入S2,直到遇到右括号为止，此时将这一对括号丢弃；

  6. 重复步骤2至5,直到表达式的最左边；

  7. 将S1中剩余的运算符依次弹出并压入S2;

  8. 依次弹出S2中的元素并输出，结果即为中缀表达式对应的前缀表达式。

        虽然规则很复杂，但是编码难度并不是很大，大家可以按照自己的技术能力尝试一下。

分析思路

        我们以表达式1+(2+3)*4-5举例。

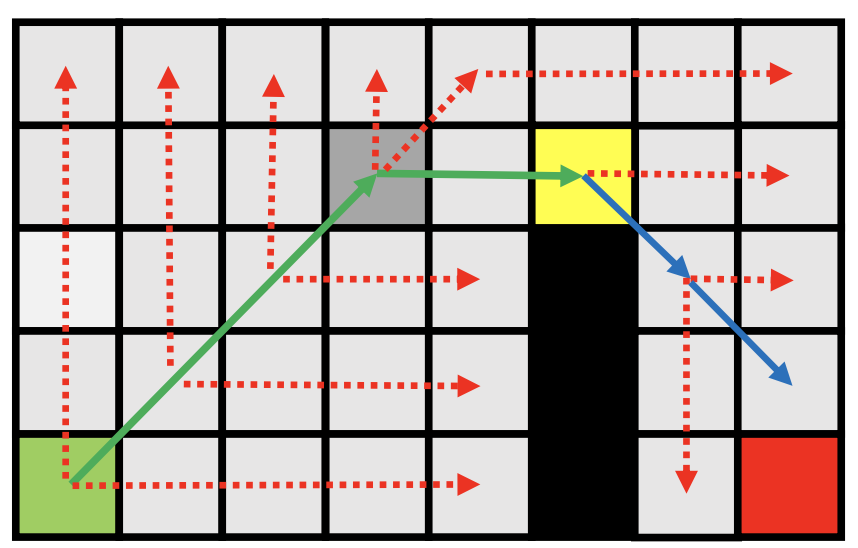
        1. 因为输入表达式是字符串，后续我们需要从右往左扫描表达式，因此首先需要将字符串表达式中的运算符和操作数进行区分，可以用整型数组如下图：

        2. 根据2至5规则，进行分析。

       

        3. 弹出S2中的数据元素：- + 1 * + 2 3 4 5;

代码示例

我的代码示例如下：

#include<stdlib.h>
#include<stdio.h>
#include<string.h>
#include<stdint.h>
#include<stdbool.h>#define STACK_LEN 1024/** 中缀表达式栈*/
static int32_t g_infix_expression[1024] = {0};/** 前缀表达式栈*/
static int32_t g_prefix_expression[1024] = {0};/** 后缀表达式栈*/
static int32_t g_suffix_expression[1024] = {0};/*** @brief 将输入的字符串表达式转换为中缀表达式** @param [in] expression 字符串表达式* @return int 0 成功 non-0 失败* */
int expression2infix(const char* expression)
{if(expression == NULL){printf("input error\n");return -1;}int dataTmp = 0; //表达式中的操作数bool dataFlag = false; // 操作数标识,表示当前是否有数据需要入栈const char* ptr = expression;int32_t* infix_index = g_infix_expression;printf("expression = %s\n",expression);while(*ptr != '\0'){/** 字符为数字*/if('0' <= *ptr  && *ptr <= '9'){dataTmp = dataTmp*10 +(*ptr - '0');dataFlag = true;}/**字符为操作符或括号*/else if(*ptr == '+' || *ptr == '-' || *ptr == '*' || *ptr == '/' || *ptr == '(' || *ptr == ')'){if(dataFlag == true){*(infix_index++) = dataTmp;dataFlag = false;dataTmp = 0;}*(infix_index++) = *ptr;}else{printf("wrong exptrssion\n");return -1;}ptr++;}/**将最后一个操作数，入栈*/if(dataFlag == true){*(infix_index++) = dataTmp;dataFlag = false;dataTmp = 0;}return 0;
}/*** @brief 将中缀表达式转换为前缀表达式** @return int 0 成功 non-0 失败* */
int infix2prefixExpression()
{/**初始化运算符栈和中间结果栈*/int32_t stack_s1[STACK_LEN] = {0};int32_t stack_s1_top = 0;int32_t stack_s2[STACK_LEN] = {0};int32_t stack_s2_top = 0; int32_t * index = g_infix_expression;/**获取中缀表达式最右侧操作数*/while(*(index+1) != 0){index++;}while(index != g_infix_expression){/** 操作符*/if(*index == '+' || *index == '-' || *index == '*' || *index == '/'){while(true){/**S1为空，或栈顶运算符为右括号)，则将此运算符入栈*/if(stack_s1_top == 0 || stack_s1[stack_s1_top-1] == ')' || stack_s1[stack_s1_top-1] == '-'|| stack_s1[stack_s1_top-1] == '+'){stack_s1[stack_s1_top++] = *index;break;}stack_s2[stack_s2_top++] = stack_s1[stack_s1_top-1];stack_s1[stack_s1_top-1] = 0;stack_s1_top = stack_s1_top -1;}}/**左括号* 则依次弹出S1栈顶的运算符，并压入S2,直到遇到右括号为止*/else if(*index == '('){while(true){/**异常*/if(stack_s1_top == 0){printf("infix experssion worong\n");return -1;}/**遇到右括号,丢弃括号*/if(stack_s1[stack_s1_top-1] == ')'){stack_s1[stack_s1_top-1] = 0;stack_s1_top = stack_s1_top -1;break;}/**其它符号需要入栈S2*/else{stack_s2[stack_s2_top++] = stack_s1[stack_s1_top-1];stack_s1[stack_s1_top-1] = 0;stack_s1_top--;}}}/**右括号* 直接入运算符栈s1*/else if(*index == ')'){stack_s1[stack_s1_top++] = *index;}/** 操作数* 直接加入栈s2*/else{stack_s2[stack_s2_top++] = *index;}index--;
#if 0printf("==============\n");printf("stack_s1=");for(int i = 0 ; i < stack_s1_top; i++){(stack_s1[i] > 9) ? (printf("%c ",stack_s1[i])):(printf("%d ",stack_s1[i]));}printf("\n");printf("stack_s2=");for(int i = 0 ; i < stack_s2_top; i++){(stack_s2[i] > 9) ? (printf("%c ",stack_s2[i])):(printf("%d ",stack_s2[i]));}printf("\n");
#endif  }/**将最左侧操作数压入s2*/stack_s2[stack_s2_top++] = *index;/**将s1中的符号压入s2*/for(int i = stack_s1_top - 1; i >= 0; i-- ){stack_s2[stack_s2_top++] = stack_s1[i];stack_s1[i] = 0;    }/**将s2中的数据弹出，放入前缀表达式栈中*/for(int i = 0 ; stack_s2_top > 0; i++,stack_s2_top--){g_prefix_expression[i] = stack_s2[stack_s2_top-1];}return 0;
}int main(int argc,char* argv[])
{if(argc != 2){printf("please input experssion\n");return -1;}int32_t iRet = 0;iRet = expression2infix(argv[1]);if(iRet == 0){for(int i = 0 ; i < STACK_LEN && g_infix_expression[i] != 0; i++){if(g_infix_expression[i] == '+' || g_infix_expression[i] == '-' || g_infix_expression[i] == '*' || g_infix_expression[i] == '/'){printf("%c ",g_infix_expression[i]);}else{printf("%d ",g_infix_expression[i]);}}printf("\n");}iRet = infix2prefixExpression();if(iRet == 0){for(int i = 0 ; i < STACK_LEN && g_prefix_expression[i] != 0; i++){if(g_infix_expression[i] == '+' || g_infix_expression[i] == '-' || g_infix_expression[i] == '*' || g_infix_expression[i] == '/'){printf("%c ",g_infix_expression[i]);}else{printf("%d ",g_infix_expression[i]);}}printf("\n");}prefixExpressionCaculate();return 0;
}

前缀表达式计算

前缀表达式的计算规则如下：

  1. 从右至左扫描表达式；

  2. 遇到数字，压入栈中；

  3. 遇到运算符，弹出栈顶的两个数，并用运算符对这两个数做相应的计算，并将结果入栈；

  4. 重复上述2,3步骤，直到表达式最左端，最后的值为表达式的结果。

分析思路

        以上述后缀表达式举例:- + 1 * + 2 3 4 5。

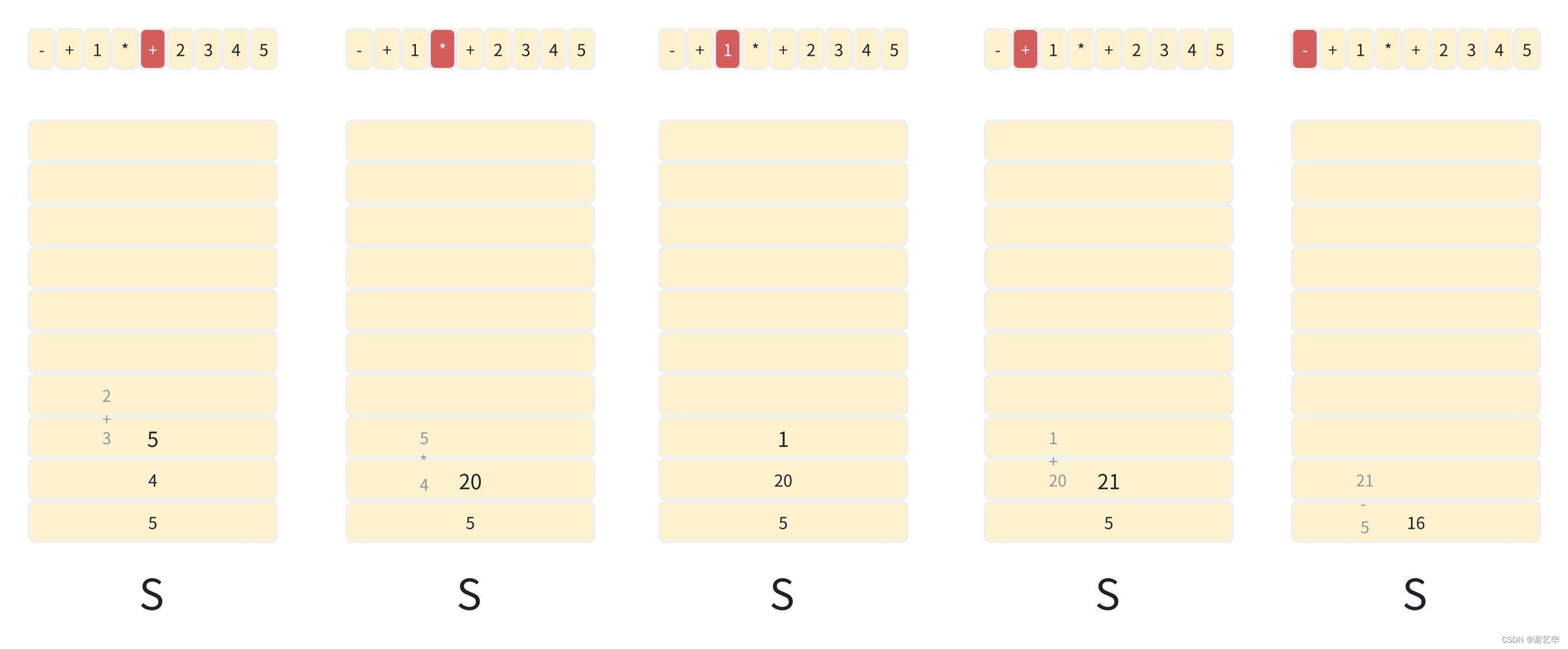
        得出结果为16。

代码示例

新增prefixExpressionCaculate接口。代码如下：

/*** @brief 将前缀表达式进行计算** @return int 0 成功 non-0 失败* */
int prefixExpressionCaculate()
{/**结果栈*/int32_t stack[1024] = {0};int32_t stack_len = 0;/**临时结果*/int32_t tmpResult = 0;int32_t data1 = 0;int32_t data2 = 0;/**获取后缀表达式的最右侧操作数*/int32_t* index = g_prefix_expression;while(*(index+1) != 0){index++;}while(index >= g_prefix_expression){/**弹出栈顶的两个数，并用运算符对这两个数做相应的计算，并将结果入栈*/if(*index == '+' || *index == '-' || *index == '*' || *index == '/'){data1 = stack[stack_len-1];data2 = stack[stack_len-2];if(*index == '+'){tmpResult = data1 + data2;}else if(*index == '-'){tmpResult = data1 - data2;}else if(*index == '*'){tmpResult = data1 * data2;}else if(*index == '/'){tmpResult = data1 / data2;}else{printf("worng prefixExperssion\n");return -1;}stack[stack_len-1] = 0;stack[stack_len-2] = tmpResult;stack_len --;}/**遇到数字，压栈*/else{stack[stack_len] = *index;stack_len ++;}index --;}printf("result = %d\n",stack[0]);return 0;
}

演示

后缀表达式

        后缀表达式与前缀表达式类似，只是运算符位于两个相应操作数之后，后缀表达式也称为后缀记法或逆波兰式。同样，我们需要解决两个问题。

  1. 如何将中缀表达式转换为后缀表达式

  2. 后缀表达式的计算规则

中缀表达式转后缀表达式

根据文中描述，中缀表达式转换为后缀表达式的规则如下：

  1. 初始化两个栈：运算符栈S1和存储中间结果的栈S2;

  2. 从左至右扫描中缀表达式；

  3. 遇到操作数时，将其压入S2;

  4. 遇到运算符时，比较其与S1栈顶运算符的优先级；

    1. 如果S1为空，或栈顶运算符为左括号(，则将此运算符入栈；

    2. 否则，若优先级比栈顶运算符的高，也将运算符压入S1;(注意是必须为高，相同或低于都不行)

    3. 否则，将S1栈顶的运算符弹出并压入到S2,再次转到4.2与S1中新的栈顶运算符相比较；

  5. 遇到括号时：

    1. 如果是左括号(，则直接压入S1;

    2. 如果是右括号)，则依次弹出S1栈顶的运算符，并压入S2,直到遇到左括号为止，此时将这一对括号丢弃；

  6. 重复步骤2至5,直到表达式的最右边；

  7. 将S1中剩余的运算符依次弹出并压入S2;

  8. 依次弹出S2中的元素并输出，结果即为中缀表达式对应的后缀表达式。

后缀表达式计算规则

后缀表达式的计算规则如下：

  1. 从左至右扫描表达式；

  2. 遇到数字，压入栈中；

  3. 遇到运算符，弹出栈顶的两个数，并用运算符对这两个数做相应的计算，并将结果入栈；

  4. 重复上述2,3步骤，直到表达式最右端，最后的值为表达式的结果。

        后缀表达式的代码示例可以参考前缀表达式的分析思路和代码，大家可以尝试编写。

总结

        时间流逝，在竞争激烈的社会背景下，我们的身处IT行业，不断逼迫自己去学习，去成长。但是总会觉得自己做的还不够。为什么总是赶不上别人的脚步，陷入怀疑自我的处境。

        朋友们，偶尔回头看看来时路上的自己，你会发现，你一直在成长，你的努力一直是正向反馈着你，不要轻视自己的努力。感谢csdn给予记录成长的平台，也感谢一直努力的自己。共勉~

参考文档

前缀表达式、中缀表达式和后缀表达式 - 乘月归 - 博客园

数据结构和算法（六）：前缀、中缀、后缀表达式

栈实现计算器-CSDN博客

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/199184.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Nodejs--Express框架使用

Nodejs--Express框架使用

目录 一.概念 二.项目目录结构 三.app.js 四.项目需要的中间件 五.Mysql连接 六.日志配置 七.实体模型配置 八.统一结果封装 九.app.js的详细配置 十.自定义登录拦截器 十一.route路由配置 十二.controller处理 十二&#xff1a;静态页面&#xff1a; 十三&#xff…
阅读更多...
高防CDN为什么可以防DDOS攻击

高防CDN为什么可以防DDOS攻击

CDN的全称是ContentDeliveryNetwork&#xff0c;即内容分发网络&#xff0c;顾名思义&#xff0c;它是一个分布式节点网络(也称为边缘服务器)&#xff0c;CDN节点具有缓存内容的功能&#xff0c;使用户可以在不获取源服务器数据的情况下就近获取所需内容&#xff0c;提高客户访…
阅读更多...
SpringCloud微服务通信两种方式Feign和Dubbo：Feign基本使用、自定义配置、使用优化；Dubbo基本实现

SpringCloud微服务通信两种方式Feign和Dubbo：Feign基本使用、自定义配置、使用优化；Dubbo基本实现

RestTemplate存在的问题 代码可读性差&#xff0c;编程体验不统一参数复杂&#xff0c;URL难以维护 Feign远程调用 Feign简介 ​ Feign是SpringCloud提供的一个声明式的伪Http客户端&#xff0c;它使得调用远程服务就像调用本地服务一样简单&#xff0c;只需要创建一个接口…
阅读更多...
Python如何实现原型设计模式？什么是原型设计模式？Python 原型设计模式示例代码

Python如何实现原型设计模式？什么是原型设计模式？Python 原型设计模式示例代码

什么是原型&#xff08;ProtoType&#xff09;设计模式&#xff1f; 原型模式&#xff08;Prototype Pattern&#xff09;是一种创建型设计模式&#xff0c;旨在通过复制现有对象来创建新对象&#xff0c;而无需通过标准的构造方式。它允许我们基于现有对象创建新对象&#xf…
阅读更多...
计算机毕业设计 基于SpringBoot的企业内部网络管理系统的设计与实现 Java实战项目 附源码+文档+视频讲解

计算机毕业设计 基于SpringBoot的企业内部网络管理系统的设计与实现 Java实战项目 附源码+文档+视频讲解

博主介绍&#xff1a;✌从事软件开发10年之余&#xff0c;专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ &#x1f345;文末获取源码联系&#x1f345; &#x1f447;&#x1f3fb; 精…
阅读更多...
《rPPG》——（1）PyTorch——Windows环境配置

《rPPG》——（1）PyTorch——Windows环境配置

《rPPG》——&#xff08;1&#xff09;PyTorch——Windows环境配置 如何查看电脑是否已安装Python环境以及Python版本 anaconda对应python3.8的版本号是多少? 强烈建议大家安装最新版的anaconda&#xff0c;虽然最新版的anaconda是Python3.11的&#xff0c;但是这个并不会影…
阅读更多...
java源码-工程讲解

java源码-工程讲解

说明&#xff1a; 源码工程目录讲解部分&#xff0c;讲解过程会让大家对后端源码工程有一个大致的了解&#xff0c;能让大家在此改造&#xff0c;就可以衍生出一些新的功能&#xff0c;需要对java技术深入了解&#xff0c;需要看后续java技术讲解部分&#xff0c;源码也是以前很…
阅读更多...
uniapp Android如何授权打开系统蓝牙Bluetooth？

uniapp Android如何授权打开系统蓝牙Bluetooth？

uniapp Android如何授权打开系统蓝牙&#xff1f; 使用uniapp开发蓝牙项目过程中&#xff0c;涉及到检测手机系统蓝牙是否打开功能&#xff0c;这里介绍Android&#xff0c;iOS暂时没有找到优方法。朋友们如果有好的方案&#xff0c;欢迎评论分享~ 文章目录 uniapp Android如何…
阅读更多...
设计模式-责任链-笔记

设计模式-责任链-笔记

动机&#xff08;Motivation&#xff09; 在软件构建过程中&#xff0c;一个请求可能被多个对象处理&#xff0c;但是每个请求在运行时只能有个接受者&#xff0c;如果显示指定&#xff0c;将必不可少地带来请求者与接受者的紧耦合。 如何使请求的发送者不需要指定具体的接受…
阅读更多...
Elasticsearch备份与还原：使用elasticdump

Elasticsearch备份与还原：使用elasticdump

在数据管理的世界里&#xff0c;备份和还原数据是重中之重的日常工作&#xff0c;特别是对于Elasticsearch这样的强大而复杂的搜索引擎。备份不仅可以用于灾难恢复&#xff0c;还可以在数据迁移、测试或者升级等场景中发挥重要作用。 在本博客中&#xff0c;我们将会重点介绍如…
阅读更多...
达梦数据库常用参数查询

达梦数据库常用参数查询

字符集 字符是各种文字和符号的统称&#xff0c;包括各个国家文字、标点符号、表情、数字等等。 字符集 就是一系列字符的集合。字符集的种类较多&#xff0c;每个字符集可以表示的字符范围通常不同&#xff0c;就比如说有些字符集是无法表示汉字的。 常见的字符集有 ASCII、G…
阅读更多...
基于Springboot的地方美食分享网站(有报告)。Javaee项目，springboot项目。

基于Springboot的地方美食分享网站(有报告)。Javaee项目，springboot项目。

演示视频&#xff1a; 基于Springboot的地方美食分享网站(有报告)。Javaee项目&#xff0c;springboot项目。 前些天发现了一个巨牛的人工智能学习网站&#xff0c;通俗易懂&#xff0c;风趣幽默&#xff0c;忍不住分享一下给大家。点击跳转到网站。 项目介绍&#xff1a; 采用…
阅读更多...
C++设计模式——单例模式

C++设计模式——单例模式

单例设计模式 应用场景特点设计模式分类懒汉设计模式饿汉设计模式使用编写的测试代码运行结果 应用场景 当多个类都需要调用某一个类的一些公共接口&#xff0c;同时不想创建多个该类的对象&#xff0c;可以考虑将该类封装为一个单例模式。 特点 单例模式的特点&#xff1a;…
阅读更多...
竞赛 题目：基于深度学习的中文对话问答机器人

竞赛 题目：基于深度学习的中文对话问答机器人

文章目录 0 简介1 项目架构2 项目的主要过程2.1 数据清洗、预处理2.2 分桶2.3 训练 3 项目的整体结构4 重要的API4.1 LSTM cells部分&#xff1a;4.2 损失函数&#xff1a;4.3 搭建seq2seq框架&#xff1a;4.4 测试部分&#xff1a;4.5 评价NLP测试效果&#xff1a;4.6 梯度截断…
阅读更多...
有Mac或无Mac电脑通用的获取安卓公钥的方案

有Mac或无Mac电脑通用的获取安卓公钥的方案

从2023年9月开始&#xff0c;所有上架应用市场的app都需要进行APP备案。 其中后端服务器在阿里云的可以在阿里云备案&#xff0c;后端服务器在腾讯云的可以在腾讯云备案。但无论你是在什么云厂商里做备案&#xff0c;无一例外的是&#xff0c;无论是上架安卓应用还是上架IOS应…
阅读更多...
释放机器人潜力，INDEMIND深耕底层技术

释放机器人潜力，INDEMIND深耕底层技术

市场转暖&#xff0c;但攘外需要同时安内。 市场降温之后&#xff0c;正迎来拐点 疫情之后&#xff0c;经济逐渐下行&#xff0c;服务机器人的“好日子”也随之结束&#xff0c;整个行业都在动荡中经历渡劫。根据TE智库报告显示&#xff0c;从2022年开始&#xff0c;我国服务…
阅读更多...
详解自动化测试之 Selenium

详解自动化测试之 Selenium

目录 1. 什么是自动化 2.自动化测试的分类 3. selenium&#xff08;web 自动化测试工具&#xff09; 1&#xff09;选择 selenium 的原因 2&#xff09;环境部署 3&#xff09;什么是驱动&#xff1f; 4. 一个简单的自动化例子 5.selenium 常用方法 5.1 查找页面元素&…
阅读更多...
获取阿里云Docker镜像加速器

获取阿里云Docker镜像加速器

1、阿里云官网&#xff08;www.aliyun.com&#xff09;注册账号 2、打开“控制台首页” 控制台首页地址&#xff1a;https://home.console.aliyun.com/home/dashboard/ProductAndService 3、点击“概览->容器镜像服务 ACR” 4、打开“镜像工具->镜像加速器”页面&#x…
阅读更多...
Motion Plan之搜素算法笔记

Motion Plan之搜素算法笔记

背景&#xff1a; 16-18年做过一阵子无人驾驶&#xff0c;那时候痴迷于移动规划&#xff1b;然而当时可学习的资料非常少&#xff0c;网上的论文也不算太多。基本就是Darpa的几十篇无人越野几次比赛的文章&#xff0c;基本没有成系统的文章和代码讲解实现。所以对移动规划的认…
阅读更多...
Java Web——JS中的BOM

Java Web——JS中的BOM

1. Web API概述 Web API 是指浏览器提供的一套接口&#xff0c;这些接口允许开发人员使用 JavaScript&#xff08;JS&#xff09;来操作浏览器功能和页面元素。通过 Web API&#xff0c;开发人员可以与浏览器进行交互&#xff0c;以实现更复杂的功能和效果。 1.1. 初识Web AP…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023