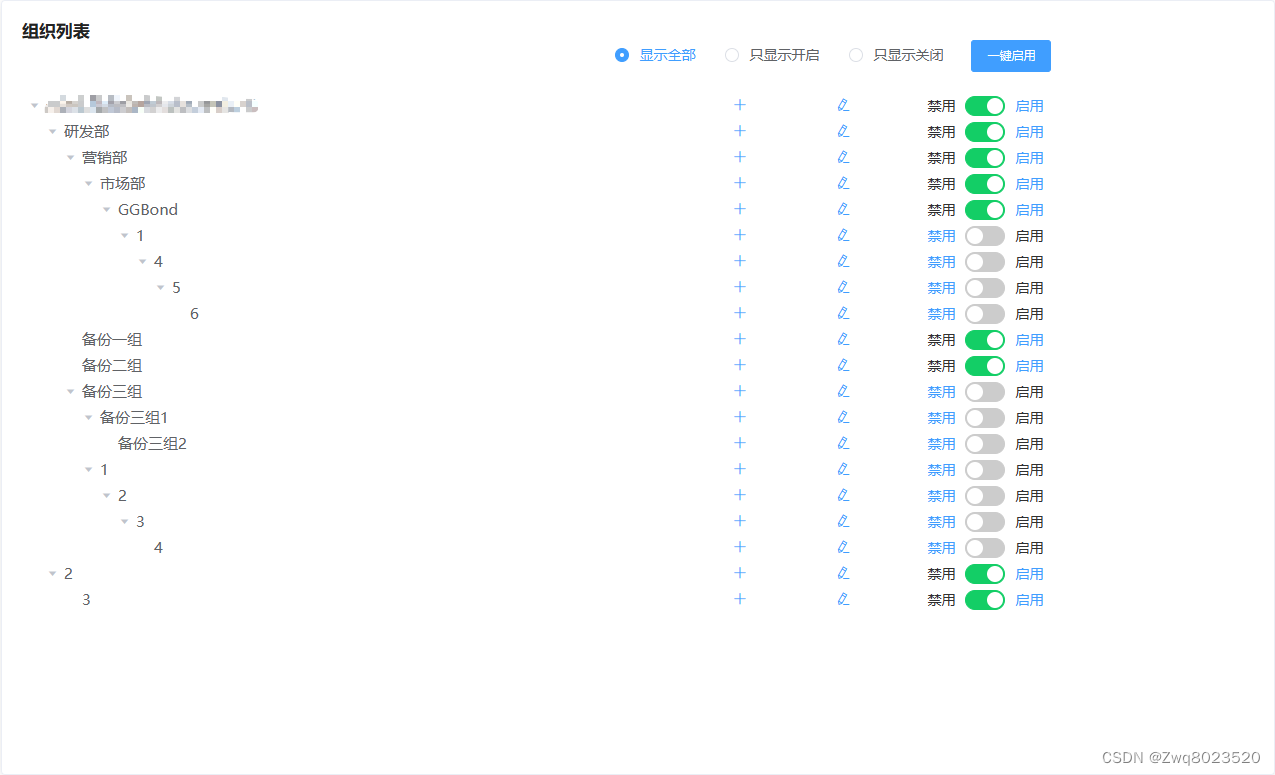
CrossEntropy loss
- 交叉熵是用来衡量两个概率分布之间的差异性或不相似性的度量
- 交叉熵定义为两个概率分布p和q之间的度量。其中,p通常是真实分布,而q是模型预测的分布

- 交叉熵还等于信息熵 + 相对熵

- 这里,x遍历所有可能的事件,p(x)是真实分布中事件 发生的概率,而q(x)是模型预测该事件发生的概率
Negative log Likelihodd loss
似然(Likelihood)
似然是在给定特定模型参数的情况下,观察到当前数据的概率。如果模型参数用0表示,观察
到的数据用X表示,那么似然通常写作L(θ|X)或P(X|θ)。
最大似然估计(MLE)就是寻找能最大化观察到的数据似然的参数值
公式
- 假设有一个统计模型,其参数为0,并且有一组观测数据X={X1,X2,X3,…Xn}。似然函数L(θ|X)定义为给定参数θ下观测数据X出现的概率:
L(θ|X)= P(X|θ) - 对于独立同分布的数据点,似然可以表示为各个数据点概率的乘积
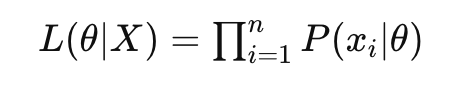
对数似然(Log-Likelihood)
对数似然是似然的对数形式,通常表示为1ogL(θ|X),对数变换是单调的,不改变似然函数
的最优参数位置。
对数变换通常在数学处理上更方便。特别是当似然是多个概率的乘积时,对数变换可以将乘法转化为加法,简化计算。
在最大似然估计中,通常最大化对数似然而不是似然,因为这在数学上更容易处理。
- 对数似然是似然函数的自然对数,它在数学处理上更方便,尤其是将乘法转换为加法。对数似然表示为:
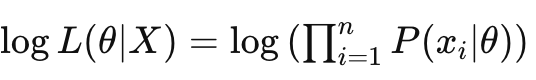
负对数似然(Negative Log-Likelihood, NLL)
负对数似然是对数似然的负值,表示为—logL(θ|X),这种形式在优化问题中更为常见。
负对数似然常用作损失函数,由于优化算法通常设计为最小化一个函数,将对数似然取负值可以将似然最大化问题转化为最小化问题
- 负对数似然是对数似然的负值,常用作损失函数,特别是在最大似然估计中。它的表达式是:
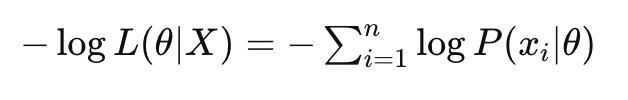
交叉熵就是负对数似然
- 似然可以写为各个数据点的概率乘积

- 除以N取平均,再log变成为加,变为对数似然,刚好变为负交叉熵定义式

KL(Kullback–Leibler) divergence也叫相对熵

- 带入均值和标准差

交叉熵等于信息熵+KL散度
信息熵
-
它是衡量信息量的一个度量,或者更精确地说,是衡量随机变量不确定性的度量
-
熵高意味着随机变量的不确定性高,熵低则意味着不确定性低。例如,如果一个随机变量只能取一个值,那么其熵为0,因为这个事件发生的概率是1,没有不确定性
-
当所有可能事件都具有相同概率时,熵达到最大值,表示最大的不确定性。

-
p是真实分布,q是预测的分布


-
当在做一个机器学习目标函数时,用交叉熵或KLD单独来看效果是一样的,因为信息熵如果是一个delta(one-hot)分布,那它的值就是0,如果是一个非delta分布,那它也是一个常数,常数对于神经网络的参数更新是没有任何贡献的,所以优化交叉熵loss和KLDloss效果是一样的,只不过数值上不一样(如果目标是delta分布,那数值也一样,这个时候用KLD时把target转换为one-hot向量就可以了)
Binary Cross Entropy二分类交叉熵
- NLLloss 是BCEloss 的一般形式,所以,可以用NLLloss代替BCEloss来算
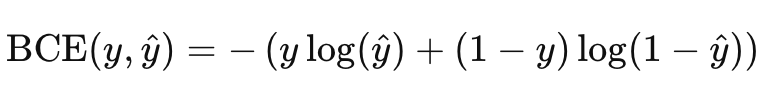


调用cosine similarity loss 余弦相似度
- 余弦相似度是一种用于衡量两个非零向量在方向上的相似程度的度量
- 可以用来做图片的相似,比如拿一个图片,想要在1百万张图片两找出前100个相似的图片,可以先用resnet等方法得到它的向量表征,然后拿这个图片的向量表征去和这1百万张做余弦相似度,然后得出最相近的前一百个即可
- 余弦值的范围在 -1 到 1 之间,其中 1 表示两个向量方向完全相同,-1 表示两个向量方向完全相反,0 表示向量之间的角度是 90 度,即它们正交或不相关
- 余弦相似度衡量的是方向上的相似性,而不是大小上的相似性。这意味着它会忽略两个向量的长度或大小,只关注它们的方向
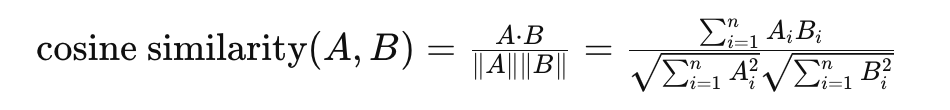
学习资料:https://www.bilibili.com/video/BV1Sv4y1A7dz/