这是一棵适合搜索二叉树

🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨
🐻强烈推荐优质专栏: 🍔🍟🌯C++的世界(持续更新中)
🐻推荐专栏1: 🍔🍟🌯C语言初阶
🐻推荐专栏2: 🍔🍟🌯C语言进阶
🔑个人信条: 🌵知行合一
🍉本篇简介:>:"二叉搜索树"的模拟实现
金句分享:
✨远赴人间惊鸿宴,一睹人间盛世颜!✨

一、什么是"二叉搜索树"?

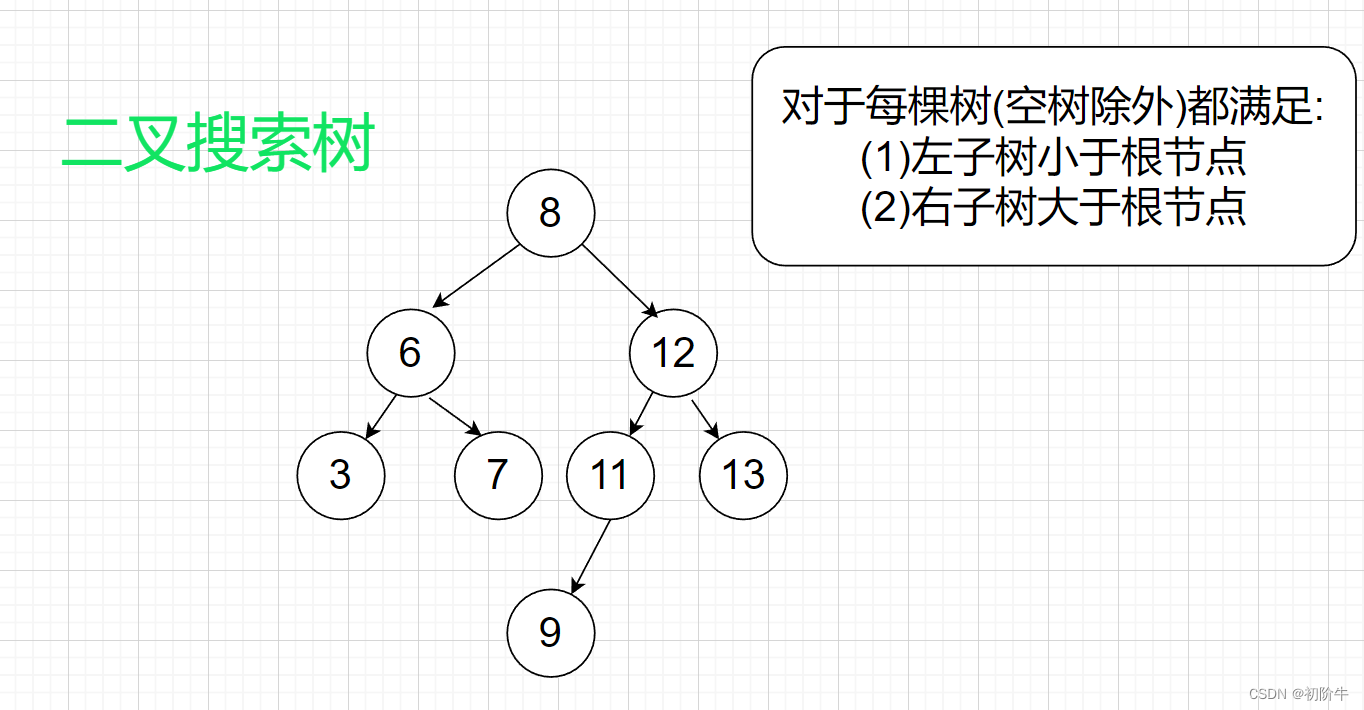
二叉搜索树（Binary Search Tree）又称为二叉查找树，是一种常用的数据结构。它是一棵空树，或者是具有以下性质的二叉树：

左子树上所有结点的值都小于它的根结点的值。
右子树上所有结点的值都大于它的根结点的值。
左右子树也分别为二叉搜索树。

错误示例1:
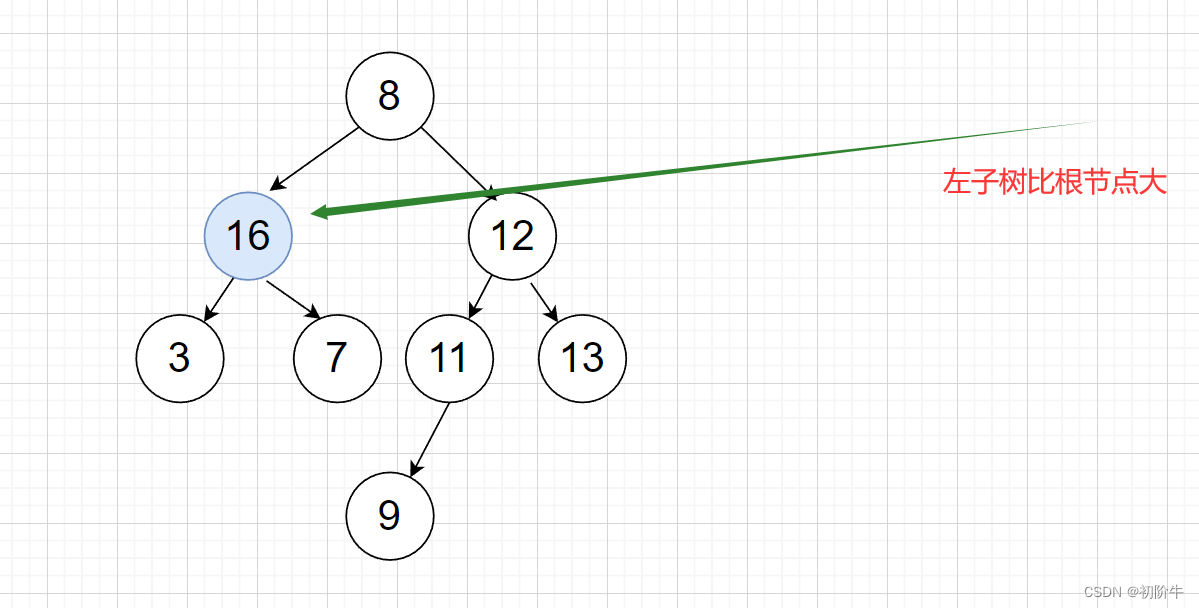
在这里插入图片描述
错误示例2:

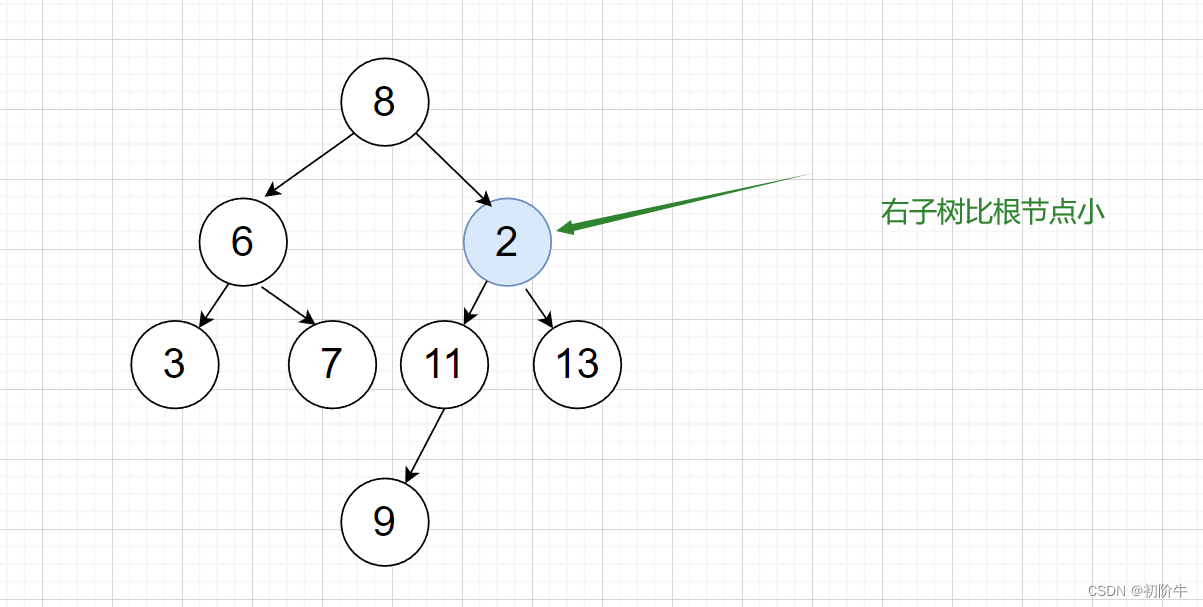
正确示例:
在这里插入图片描述

二、"二叉搜索树"的实现

本篇文章实现的是键值对也就是(key,value)版本的 “二叉搜索树”.
Key-value版本的二叉搜索树（BST）是一种基于二叉树数据结构的数据结构，其中每个节点都存储一个键-值对。在该数据结构中，每个节点都具有一个唯一的关键字，该关键字用于对节点进行排序.

如下是树中每个结点的结构:

结点结构

template<class K, class V>
struct BSTreeNode
{BSTreeNode(const K& key = K(), const V& value = V()): _left(nullptr), _right(nullptr), _key(key), _value(value){}BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;K _key;							//关键码,用于比较大小的,按key比较V _value;						//用于存储数据
};

“二叉搜索树”:的结构

template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;		//注意这里的类型重命名
public:bool Insert(const K& key, const V& value);Node* Find(const K& key);bool Erase(const K& key);void _InOrder(Node* root);void InOrder();
private:Node* _root = nullptr;
};

(1) "插入"操作

根据"二叉搜索树"的特性,我们不难知道,左子树 < 根 < 右子树.

如果是空树,则表明新插入的结点将作为根节点.
如果不是空树,则先找到该插入的位置,再链接即可.

示例:如果在插入一个结点值为9的结点.

寻找过程:
比根节点8大,所以往右找.
比12小,所以往左找.
比11小,所以往左找.
11的左边为空,寻找结束.

将9结点插入到11的左边.

在这里插入图片描述

//插入操作
template<class K, class V>
bool BSTree<K,V>::Insert(const K& key, const V& value)
{//如果是空树,则直接赋值给根节点if (_root == nullptr){//没看清node结构的,可以翻到上面在看一下构造函数._root = new Node(key,value);	//用值构建结点,并赋给根节点return true;}//如果不是 空树Node* cur = _root;			//代替根节点遍历树,寻找插入位置.Node* pnode = nullptr;		//记录目标位置的父亲结点while (cur)				//一直找到nullptr为止{pnode = cur;				//更新父节点if (key > cur->_key)		//如果插入的键值对 key 比当前元素的key大,则往右走{cur = cur->_right;}else if (key < cur->_key)		//如果插入的值比当前元素小,则往左走{cur = cur->_left;}else return false;			//相等则返回false}//判断插入在左边还是右边Node* newnode = new Node(key, value);if (key < pnode->_key){pnode->_left = newnode;}else{pnode->_right = newnode;}return true;
}

(2) "查找"操作

友友们插入操作都能轻松拿捏,那find还不是轻松拿捏?

小注意:
如果函数是在类里面声明,类外面定义,则需要注意一个小问题.
Node是一个类型还是一个变量(静态成员变量可以通过类名+ ::访问),所以需要在前面加上一个关键字typename ,告诉编译器这是一个类型.

template<class K, class V>
typename BSTree<K,V>::Node* BSTree<K, V>::Find(const K& key)
{Node* cur = _root;			//代替根节点遍历树.while (cur){if (key > cur->_key)		//如果查找的值比当前元素大,则往右走{cur = cur->_right;}else if (key < cur->_key)		//如果查找的值比当前元素小,则往左走{cur = cur->_left;}else return cur;			//相等则说明找到了}return nullptr;
}

(3) "删除"操作 (重点)

删除操作应该是"二叉搜索树"最难的操作了,这里牛牛就讲解的仔细一点吧!

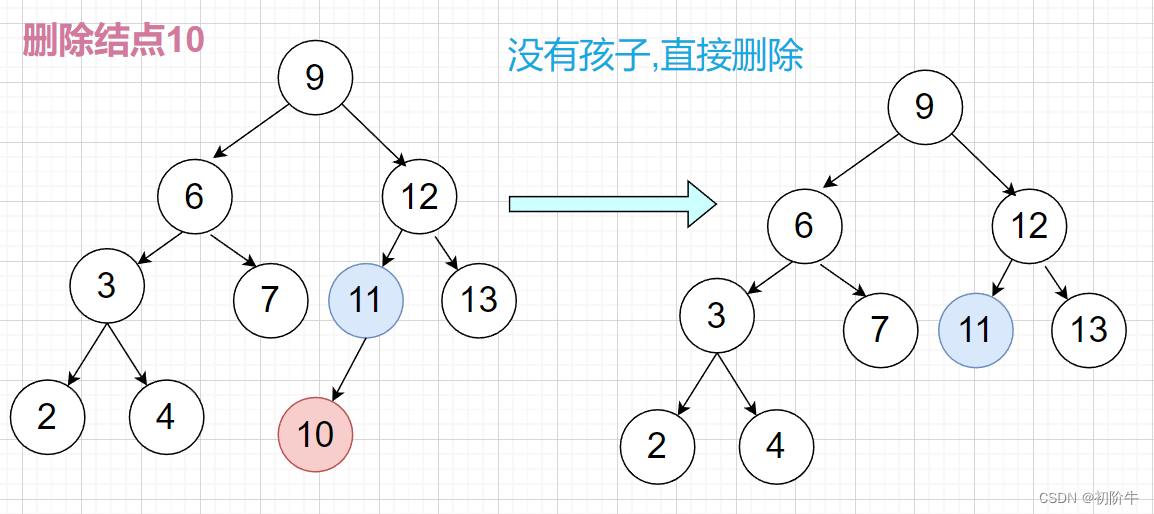
(1)情况1: 目标结点没有孩子.
处理方法:找到该结点和该结点的父亲,直接删除即可.
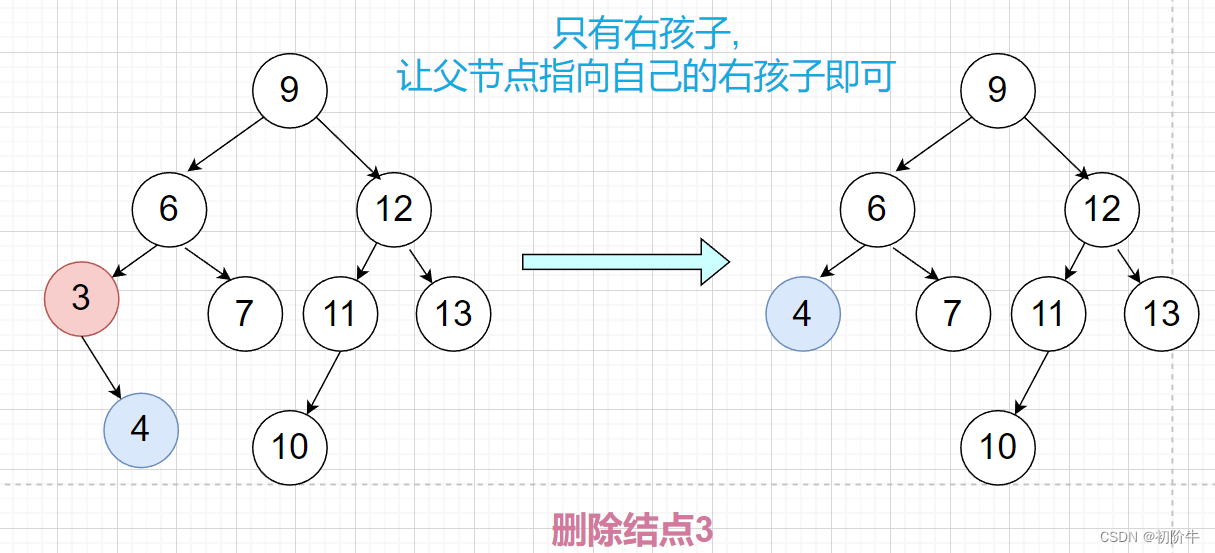
在这里插入图片描述

(2)情况2:目标结点只有一个孩子,可能是左孩子,也可能是右孩子.
处理方法:
只有左孩子时:
让父亲不再指向自己(这里要判断自己在父亲的左还是右),而是指向自己的左孩子,然后再删除自己.
在这里插入图片描述

只有右孩子时:
让父亲不再指向自己(这里要判断自己在父亲的左还是右),而是指向自己的右孩子,然后再删除自己.
在这里插入图片描述

情况3: 目标结点有两个孩子.

找右子树的最小节点:
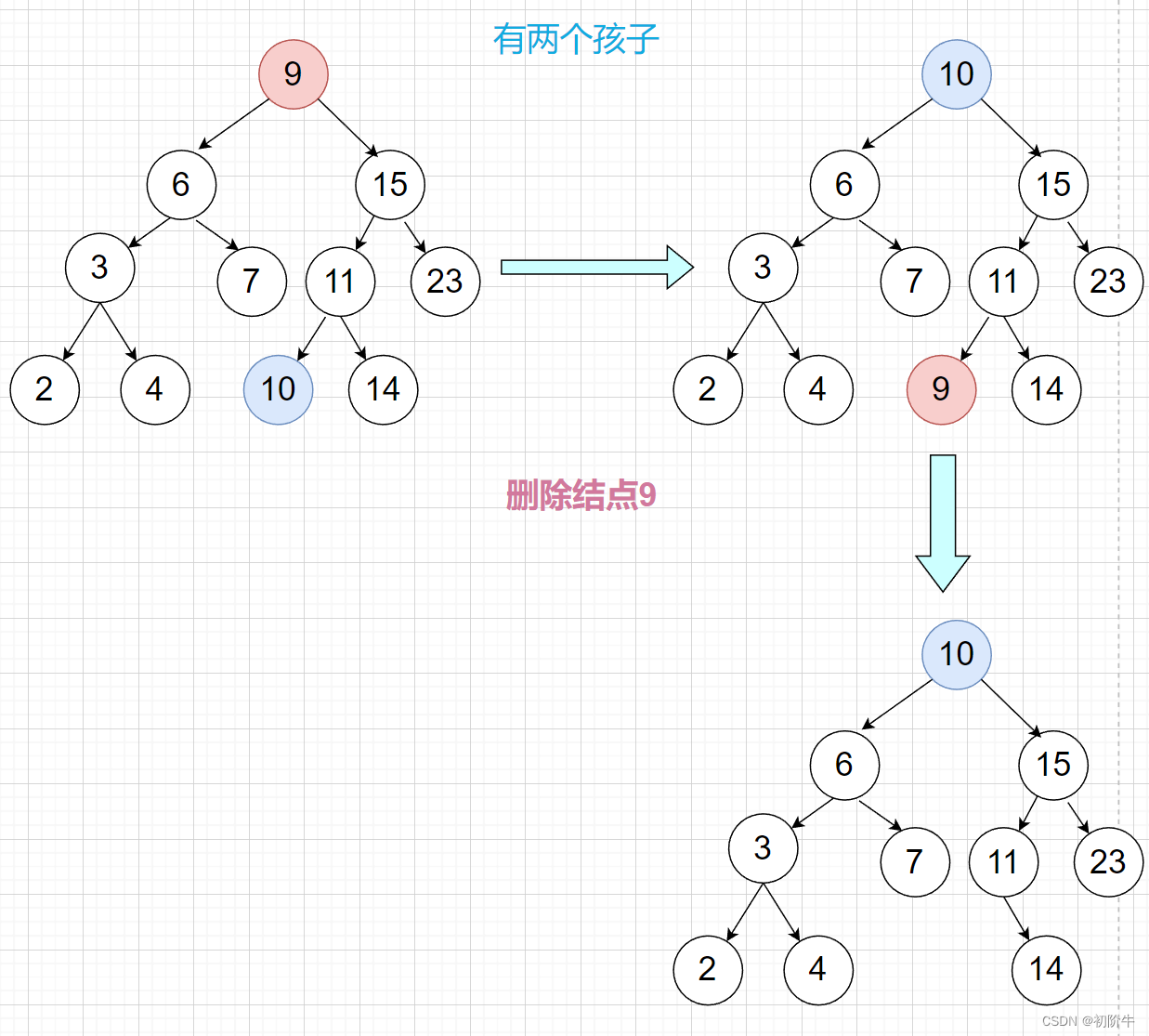
在这里插入图片描述

找左子树的最大节点:
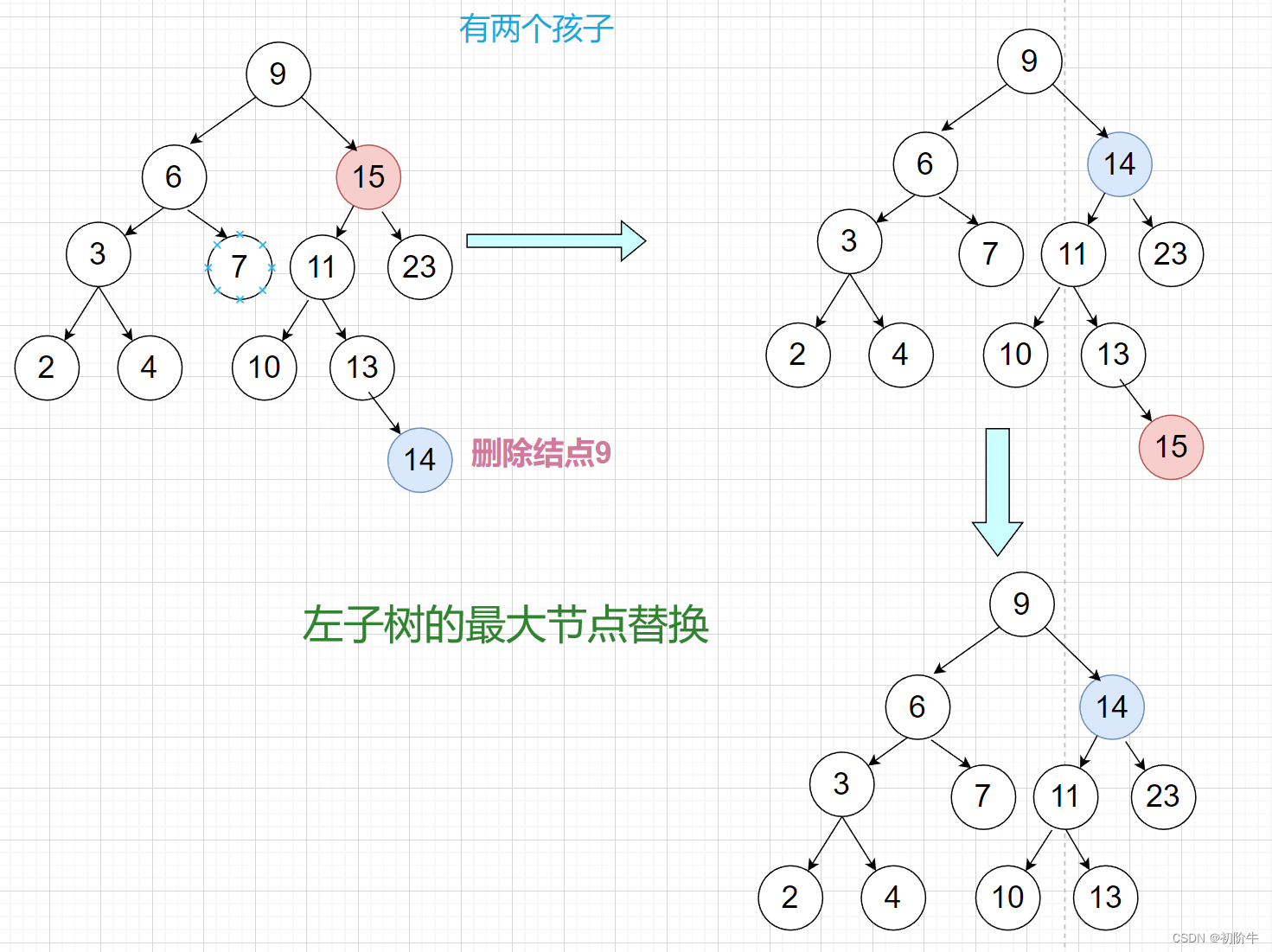
在这里插入图片描述

代码实现:

template<class K, class V>
bool BSTree<K, V>::Erase(const K& key)
{if (_root == nullptr){cout << "空树不可删除" << endl;//空树无法删除return false;}//寻找目标结点的位置Node* pnode = nullptr;		//记录当前结点的父亲结点Node* cur = _root;			//当前结点:代替根节点遍历树.//寻找目标结点while (cur){if (key > cur->_key)		//如果插入的值比当前元素大,则往右走{pnode = cur;cur = cur->_right;}else if (key < cur->_key)		//如果插入的值比当前元素小,则往左走{pnode = cur;cur = cur->_left;}else  break;			//相等则说明找到了}//表示在树中 未找到if (cur == nullptr) { return false; }//这里采取与右子树的最小结点替换的方法if (cur->_right && cur->_left)//如果有两个孩子{Node* p_left_max = nullptr;			//右树 的最小节点的父亲Node* left_max = cur->_right;		//右树 的最小节点//寻找目标结点 右树 的最小节点while (left_max->_left){p_left_max = left_max;left_max = left_max->_left;}//替换cur->_key = left_max->_key;		//其实覆盖即可cur->_value = left_max->_value;//将原右子树的最小结点的父亲与 右树最小结点断绝关系p_left_max->_left = nullptr;delete left_max;					//删除右树最小结点return true;}// 要删除的节点只有一个子节点或没有子节点Node* child = nullptr;//这样child就是孩子if (cur->_left)	//只有左孩子{child = cur->_left;}else//只有右孩子或者没有孩子{child = cur->_right;}if (pnode == nullptr) // 根节点要删除的情况_root = child;else if (pnode->_left == cur) // 要删除的节点是父节点的左子节点pnode->_left = child;else // 要删除的节点是父节点的右子节点pnode->_right = child;delete cur;return true;
}

(4)"中序"遍历

学过二叉树的友友,对于这个,没啥好说的吧.

补充小技巧.

由于我们在类外面调用中序遍历函数需要传递root结点,但是root结点是私有成员变量,在类外面无法获取.
对象名.InOrder();

优秀的解决方法:
再嵌套一层,类里面的函数可以直接获取私有成员变量root,所以我们可以利用这一点.

template<class K, class V>
void  BSTree<K, V>::InOrder()
{if (_root == nullptr){cout << "空树" << endl;return;}_InOrder(_root);		//这里调用即可
}

类中:

template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:void _InOrder(Node* root);void InOrder();
private:Node* _root = nullptr;
};

真正的中序遍历:


template<class K, class V>
void  BSTree<K, V>::_InOrder(Node* root)
{if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << "->" << root->_value << endl;_InOrder(root->_right);
}