操作环境:
MATLAB 2022a
1、算法描述
QC-LDPC(准循环低密度奇偶校验)编码是一种高效的错误校正编码方式,广泛应用于通信系统和数据存储中以提高数据的可靠性。它是低密度奇偶校验(LDPC)编码的一种特殊形式,具有更为方便的实现方式。
QC-LDPC 编码
1. 基本概念:QC-LDPC 编码基于稀疏矩阵,这种矩阵中大部分元素为零。在QC-LDPC中,这个矩阵被构造为更小的矩阵块的排列,这些小矩阵块要么是零矩阵,要么是置换矩阵(一个单位矩阵经过行或列的置换得到)。
2. 生成和校验:在QC-LDPC中,通过一个生成矩阵(G矩阵)来进行编码,它可以产生编码后的数据。同时,还有一个校验矩阵(H矩阵),它是用来检测错误和进行解码的。
3. 编码过程:编码时,原始数据与生成矩阵相乘,产生编码后的数据。这个过程添加了额外的校验位,使得整个数据具有纠错能力。
QC-LDPC 解码
1. 迭代解码:QC-LDPC 编码通常采用基于信念传播(Belief Propagation)的迭代解码算法。解码器通过校验矩阵进行多轮计算,逐步修正接收到的数据中的错误。
2. 两种节点更新:在解码过程中,涉及到变量节点(Variable Node)和校验节点(Check Node)的更新。变量节点根据校验节点提供的信息更新自身估计值,校验节点则基于变量节点的估计值来更新自己的信息。
3. 收敛判定:解码器会重复进行节点更新过程,直到数据满足校验矩阵的条件,或者达到预设的最大迭代次数。
QC-LDPC 的作用
1. 提高数据传输可靠性:QC-LDPC编码能够有效地校正传输过程中可能出现的错误,提高数据传输的准确性和可靠性。
2. 提高频谱效率:由于其高效的纠错能力,QC-LDPC编码允许在较差的信道条件下也能保持较高的数据传输率,从而提高了频谱利用效率。
3. 灵活性和适应性:QC-LDPC编码由于其准循环的结构,使得它在硬件实现上更加灵活,更容易适应不同的应用场景和要求。
2、仿真结果演示
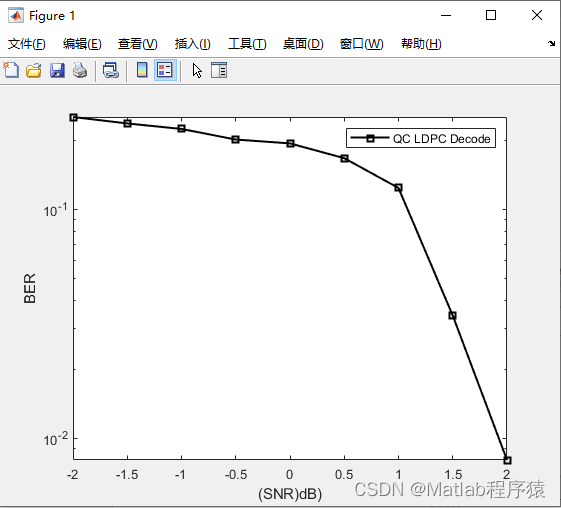
3、关键代码展示
4、MATLAB 源码获取
V
点击下方名片